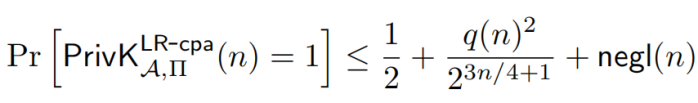一、LRTA*(K)算法的缺点

LRTA*(K)算法每次要更新队列Q里的state，但有三点缺陷：

如果state y进入 Q，但重考虑后 h(y) 不会改变，这是一种浪费时间的努力
可能有的state进入Q不止一次，要经过多次更新才能打到最终值
进入Q的state的顺序以及K的取值都会影响最终结果

下面举个栗子说明：

在这里插入图片描述
如图（i）， a, b, c, d是state，最左侧那一列是迭代次数，state下边的数字是 h 值，每次移动 g = 1，后继按左-右的顺序改变。

下边是每次迭代运行的具体步骤(一定注意是左右的顺序进入Q，然后每次迭代就是从Q里按顺序取state)：

第零次迭代：当前state是d，迭代0那一行的数字是初始 h 值，h(d)一开始是2，得先考虑d，把d加入Q，Q = {d}，这就是为什么后文说d进Q两次，这里还有一次他没写出来！
第一次迭代：h(d)=4， Q={c} -----这里就是，d改变后，考虑左边的c，右边没东西
第二次迭代：h( c ) = 5, Q={b, d} -----这里是第一次移动，移动到c点，然后考虑c左右的state{b, d}，放入Q
第三次迭代：h(b)不变 ----这里并没有移动，agent还在c，b是从Q里取出来的，看它要不要更新，下一个就取d出来。
第四次迭代：h(d) = 6, Q = {c} -----你看我说要取d出来看看要不要更新吧？d需要更新，如果d更新了，那下一个就要考虑d的后继了，那就是c，c就先进入Q
第五次迭代：h( c )不变 ----然后把c从Q取出来，c不变
然后没有需要更新的就停下了。

在这个过程中，c和d进入Q两次，d更新了两次，c只更新了一次。整个流程，一共就走了一步，走之前的整个Q={d}，走一步移动到c后，Q = {c, b, d, c}。

然后文中说，如果K=3，且还是左右顺序进入Q，那么进入Q的顺序就是d, c, b，就如图 (ii) 所示。我不理解，第一个 d 是第一步呀，为啥要加在这里？不加d的话，走了第一步到C，Q={c, b, d}，我觉得和上边结果一样的呀？不理解。。。

二、 $LRTA*_{LS}(k)$ 算法

算法概览： $LRTA*_{LS}(k)$ 算法把states分为内部states（用集合 $\in X$ 表示, X是所有state的集合）和边缘states （用集合 $\in X$ 表示）， $\cap F=\emptyset$ ， $LRTA*_{LS}(k)$ 选择当前状态的局部空间并更新其内部state, 内部states只更新一次值，内部states的数量上限为K（集合 I 的长度最高为K），该算法继承 LRTA* 和 LRTA*(K) 的良好属性。

1、选择局部空间

步骤如下：

设 $\emptyset$ , Q = {x| x是当前state}
循环直到 Q 空了或者 $∣ I ∣ = = K$ :
从Q中提取state w，如果 w 就是目标，就跳出循环。否则，检查是否存在 $min_{v \in \{Succ(w)-I\}}h(v)+g(w, v)$
其中 $h (w)$ 是state w的启发值， ${Succ(w)-I\}$ 表示w的所有后继state $S u c c (w)$ 减去 I 集合中的交集，剩下的不在 I 中的后继state，g(w, v)表示从state w 到 v 的路程代价。
如果满足上式（文中称之为“更新条件”），就把 w 加入 I，v 加入 Q
把 I 中所有state的不在I中的后继state加入边缘集合 F

下面是一个例子说明（我觉额的原文说的好像不太对呢，虽然最后结果对，但中间过程和他上边步骤里写的不太一样啊，而且一点都没提Q更新的事儿，下面是我按他的步骤+我自己理解写的，各位有兴趣可以去看看原文这部分）

在这里插入图片描述

如上图所示，state之间的路程代价 g = 1，

从 d 点开始，那么一开始 $\empty$
然后开始进入第二步的循环，从Q中取出d，判断 $min_{v \in \{Succ(w)-I\}}h(v)+g(w, v)$ ，这里的 v 就是 d 的后继，只有 c，所以 $2 < 3 + 1$ ，条件成立，把 d 加入 I，c 加入 Q
把 c 从 Q 中取出，c的后继有俩，b和d，其中d已经在 I 中了，所以只看b就行了， $3 < 4 + 1$ 也成立，那么把 c 加入 I，现在 I = {c, d}，把 b 加入 Q
把 b 从Q中取出，b也有俩后继，a和c，因为 c 在 I 中了，所以只考虑 a， $4 = 3 + 1$ ，条件不成立了，就不能把 b 加入 I，同样 a 也不能进入 Q
a 没有进入 Q，那么 Q 就空了，循环终止！
此时我们得到了内部state的集合 $I = \{c, d\}$ ，然后把c，d的不在 I 的后继加入边缘集合F={b}
程序终止！