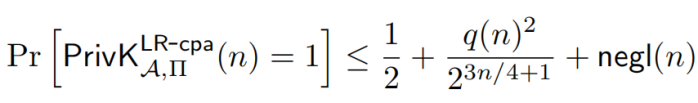目录
3.6.3分组密码及其操作模式
ECB(Electronic Code Book) 电码本模式
CBC(Cipher Block Mode) 密文分组链接方式
THEOREM 3.32 CBC模式的CPA安全
连锁CBC模式
OFB(Output Feedback Mode) 输出反馈模式
CTR(Counter) 计数器模式
THEOREM 3.33 CTR多明文PCA安全
THEOREM 3.33 的证明
3.6.3分组密码及其操作模式
分组密码只是（强）伪随机置换的另一个名称。关于伪随机置换，可参考
现代密码学导论-18-伪随机置换_南鸢北折的博客-CSDN博客
对于分组密码F
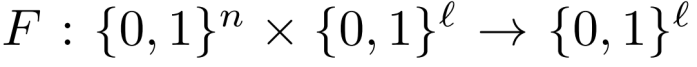
F是含参数k的，对于任意的k，有如下定义
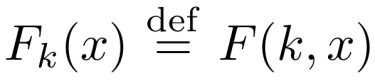
Fk是一个双射函数
n是k的长度，l是分组长度
分组密码和伪随机置换的主要区别是，前者通常只支持一组特定的key/分组长度，特别是不支持任意长度的key
为简单起见，我们将在本节中假设l=n，同时假设消息的长度是n的整数倍
消息记作下面的式子，其中mi∈{0, 1}^n
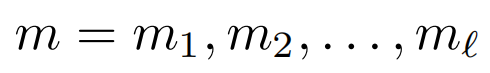
ECB(Electronic Code Book) 电码本模式
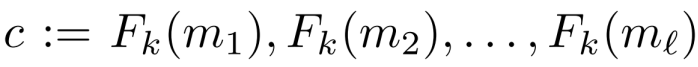由于ECB的加密方式是确定性的，因此其显然不能满足CPA安全。更糟糕的是，ECB加密甚至不满足EAV安全。这这因为如果一个分组在明文中重复，那么在密文中也会重复。因此，很容易将由两个相同分组组成的明文的加密与由两个不同分组组成的明文的加密区分开来。
上图说明了ECB加密存在的风险。中间的图是使用ECB模式对左侧图像进行加密；右边的图是使用安全模式对同一图像进行的加密。
CBC(Cipher Block Mode) 密文分组链接方式
在开始加密流程时，先随机均匀选择一个长度为n的初始向量IV，并将其作为初始密文分组，然后将当前明文分组和前一个密文分组的异或，再通过 F 函数生成新的密文分组。具体来讲，我们令
对于i从1到l
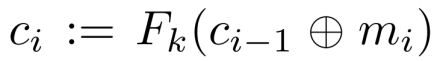
我们的到密文c为
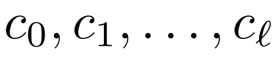
当接收方收到密文c时，解密方式如下
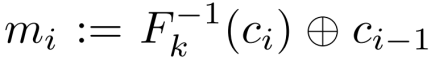
由于CBC模式在加密过程中，每次F的计算都依赖于前一次的计算结果，因此其加密过程必须按顺序执行，这意味着其不能通过并行来快速运算
THEOREM 3.32 CBC模式的CPA安全
如果F是一个伪随机置换，则CBC模式是CPA安全的
连锁CBC模式
普通的CBC模式有一种有状态的变体，即连锁CBC模式。在加密下一个消息时，前一个密文的最后一个分组被用作IV。这减少了带宽，因为不需要每次都发送一个新的IV。SSL 3.0和TLS 1.0使用这种模式
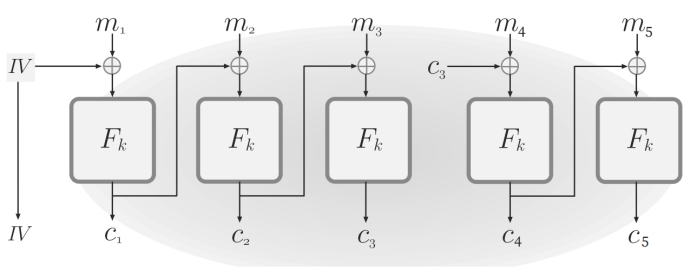
然而，链式CBC模式很容易受到选择明文攻击。
我们假设敌手A知道
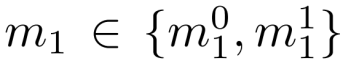
而且知道密文
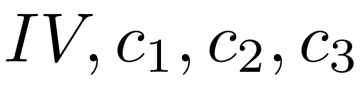
攻击者请求加密m4和m5，其中
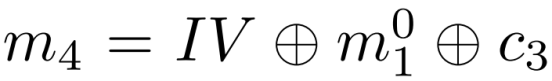
则
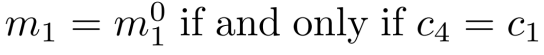
因此敌手就得到了m1
OFB(Output Feedback Mode) 输出反馈模式
要加密消息m，先随机均匀选择一个长度为n的初始向量IV。定义y0 := IV
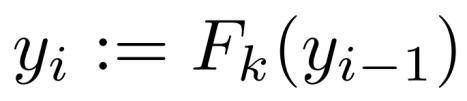
在CBC模式中，IV作为密文的一部分包含在内，以实现解密。然而，与CBC模式相比，这里并不要求F是可逆的(事实上，它甚至不需要是一种置换
如果F是一个伪随机函数，则OFB模式可以被证明是CPA安全的。
这种模式的优点在于可以在明文到来之前完成一部分yi的计算，从而提高加密的效率。
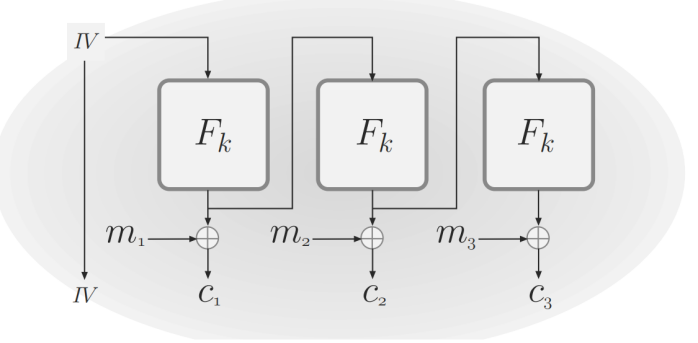
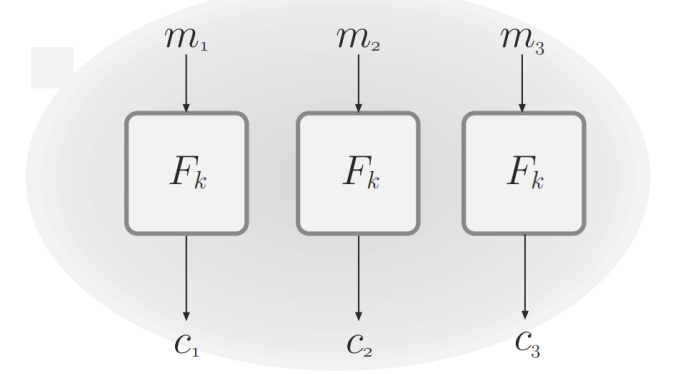
CTR(Counter) 计数器模式
加密的消息分组数l如果满足
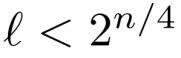
则选取的初始化向量满足
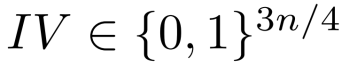
然后计算伪随机流
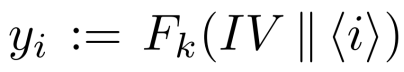
其中计数器i被编码为一个n/4位的字符串
(当然，初始向量长度和计数器编码长度可以变动，只要满足和为n即可)
第i个分组的加密方式为
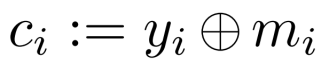
和CBC和OFB模式一样，IV作为密文的一部分包含在内，以实现解密
解密不需要F是可逆的，甚至不需要F是置换。
和前面的几种模式相比，CTR是可以完全并行化的，而且该模式还可以单独恢复第i个分组
THEOREM 3.33 CTR多明文PCA安全
如果F是一个伪随机函数，那么CTR模式是多明文PCA安全的
THEOREM 3.33 的证明
现代密码学导论-16-选择明文攻击和CPA安全_南鸢北折的博客-CSDN博客
上文中的THEOREM 3.23表明，任何PCA安全的方案同时也是多明文PCA安全的，因此我们只需证明CTR在F是伪随机函数时具有PCA安全即可
但是我们在这里不依赖于THEOREM 3.23，我们将直接证明其满足多明文PCA安全
现代密码学导论-19-基于伪随机函数的CPA安全_南鸢北折的博客-CSDN博客
我们参考上文中THEOREM 3.29 的证明
确定一个PPT敌手A，设q(n)为敌手A在安全参数为n的LR预言机实验中询问预言机的次数的多项式上界函数
现代密码学导论-16-选择明文攻击和CPA安全_南鸢北折的博客-CSDN博客
关于LR预言机实验，详见上文
假设A提交给预言机的消息的分组数l满足
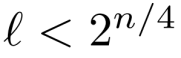
事实上，对于充分大的n，这一定是成立的，因为A是PPT的
让Π =(Gen，Enc，Dec)为CTR模式的加密方案
再构建一个新的加密方案，用真随机函数取代CTR模式中的伪随机Fk，记作
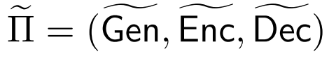
这意味着
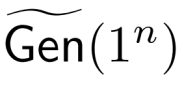
是随机均匀挑选了一个f∈Func_n
我们完全模仿3.29的证明，可以得到A式
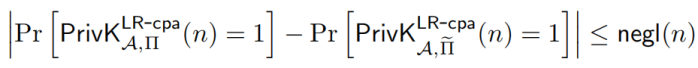
考虑实验
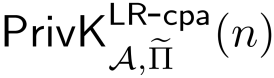
有
带入A式，得到
