【数字信号调制】16QAM信号调制解调【含Matlab源码 2050期】

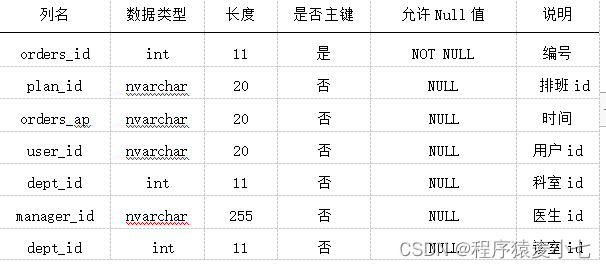
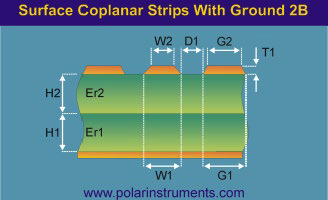
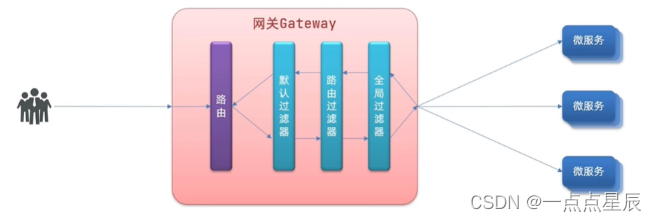
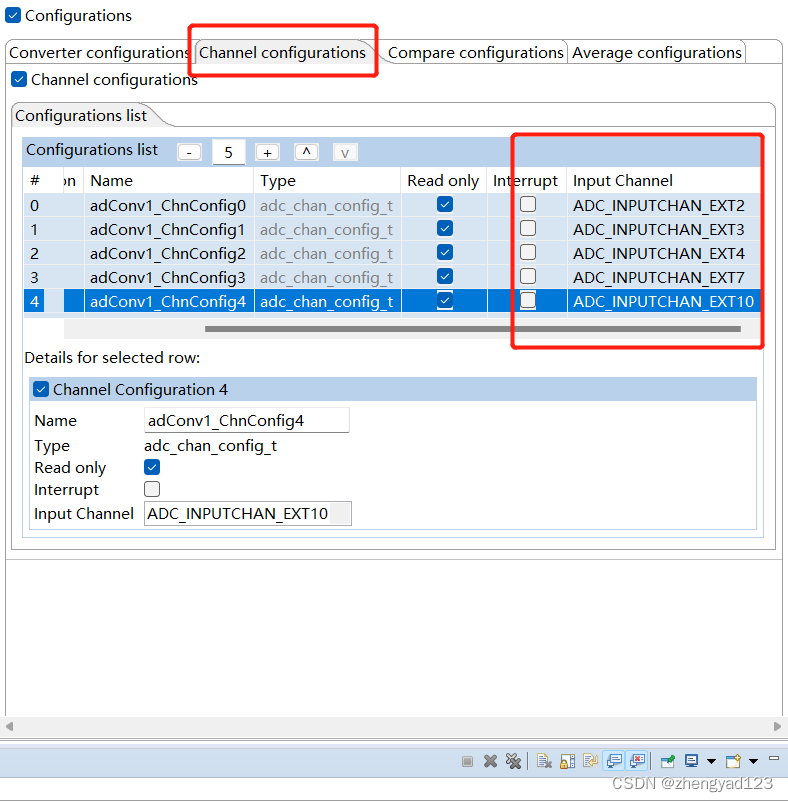
⛄一、QAM调制与解调（附实验题目说明）

1 引言
数字振幅调制、数字频率调制和数字相位调制是数字调制的基础,然而,这3种数字调制方式都存在不足之处。如频谱利用率低、抗多径衰落能力差、功率谱衰减慢、带外辐射严重等。为了改善这些不足,几十年来人们不断提出一些新的数字调制解调技术,以适应各种通信系统的要求。其主要研究内容围绕减小信号带宽以提高频谱利用率,提高功率利用率以增强抗干扰性能等。正交幅度调制解调(quadrature amplitude modulation and demodulation)就是一种高效的数字调制解调方式,他在中、大容量数字微波通信系统、有线电视网络高数据传输、卫星通信等领域被广泛应用。

单独使用振幅和相位携带信息时,不能最充分利用信号平面,这可由矢量图中信号矢量端点的分布直观观察到。多进制振幅调制时,矢量端点在一条轴上分布;多进制相位调制时,矢量点在一个圆上分布。随着进制数M的增大,这些矢量端点之间的最小距离也随之减少。但如果充分利用整个平面,将矢量端点重新合理地分布,则可能在不减小最小距离的情况下,增加信号的端点数。基于上述概念引出的振幅与相位结合的调制方式被称为数字复合调制方式,一般的复合调制称为幅相键控(APK),2个正交载波幅相键控称为正交振幅调制(QAM)。

M-QAM信号可以表示为:
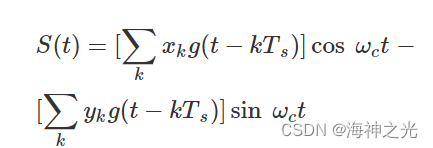
在这里插入图片描述
他是2个已调正交载波信号的和。在电路实现中,正交载波sin ωct可用同相载波cos ωct经移相π/2后得到,所以取负号。g(t)为系统的单位脉冲响应,取幅度为1,xk,yk分别表示所要传输的2路多电平信号第k个码元的值,Ts是一个码元的持续时间,ωc是载波角频率。

2 调制原理
在理想状态下,M-QAM的M个载波状态可以调制log2M个比特,如16QAM的载波状态最多可调制一个4 b的信号(log216=4),也就是说M-QAM 的频谱利用率为log2M b/s/Hz。目前星座图里的样点数,例如16QAM,确定QAM的类型,16个样点表示这是16QAM 信号,星座图里每个样点表示一种状态。16QAM有16态,每log2M=4位规定16 态中的1 态。16QAM 中规定了16 种载波幅度和相位的组合,16QAM的每个符号或周期传送4 b。解调器根据星座图及接收到载波信号的幅度和相位来判断发送端发送的信息比特。16QAM 也是二维调制技术,在实现时也采用正交调幅的方式,某星座点在I坐标上的投影去调制同相载波的幅度,在Q坐标上的投影去调制正交载波的幅度,然后将2个调幅信号相加就是所需的调相信号。

可见星座点数越大,在一个周期内可传送的数据比特数就越多,频谱利用率就越高。16QAM,32QAM,64QAM,128QAM 的频谱利用率理论值分别为4,5,6,7(单位:b/s/Hz)。此处的频谱利用率理论值是指当传输信号的频谱为理想低通频谱时所实现的频谱效率,但在实际应用中达不到这一理论效率,因为在实际应用中传输信号通常采用升余弦滚降波形,他所实现的频谱效率要比理论效率下降一个滚降系数α倍。16QAM,32QAM,64QAM,128QAM的星座图如图1所示。
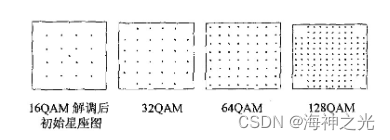
在这里插入图片描述
图1 星座图
由图1可知,当M=16或64时星座图为矩形,而M=32或128时则为十字形。前者M为2的偶次方,即每个符号携带偶数个比特信息;后者M为2的奇次方,每个符号携带奇数个比特信息。每个符号可分解为x,y两个分量,常标为同相分量和正交分量,即I,Q分量。

3 具有矩形星座图信号的调制与解调
3.1 具有矩形星座图的信号调制
输入数据序列经串并变换分成I,Q两路,再经2-L电平变换及星座图映射,形成xk,yk。M为了抑制已调信号的带外辐射,xk,yk要通过预调制低通滤波器,再分别与相互正交的2路载波相乘,形成2路ASK调制信号,最后将2路信号相加就可得到不同幅度和相位的已调QAM输出信号。

下面详细解释这部份的实现,M-QAM信号共有M个信号点,代表一个M进制信号集。每个符号用n=log2M个比特表示。使用矩形星座图时,2路正交信号的电平代码可分别用n/2 b表示.若M=16或64,n=log2M =4或6,则I,Q两路的电平代码分别用2或3 b表示,L=22或23即4或8,经2-L电平转换后I,Q两路输出的值分别由0,1,2,3或0,1,2,3,4,5,6,7组成。星座图映射完成的是将由0,1,2,3或0,1,2,3,4,5,6,7组成的数字序列分别转换成由-3,-1,1,3或-7,-5,-3,-1,1,3,5,7组成的数字序列。由此可见,I路取值电平数为M−−√,即x=±1,±3,…,±L-1。Q路的取值方法与x完全相同。

3.2 具有矩形星座图的信号解调
将输入信号分成2路分别与本地恢复的2个正交载波相乘,经过低通滤波器滤掉倍频分量得到x(t),y(t)。再根据本地恢复时钟进行多电平判决, 16QAM以±2,±0.5为判决电平,判决后得到一组由±1,±3组成的数据;64QAM以±6,±4,±2,±0.5为判决电平,判决后得到一组由±1,±3,±5,±7组成的数据。16QAM星座图反映射完成的是将±1,±3映射成为 0,1,2,3;64QAM星座图反映射完成的是将±1,±3,±5,±7 映射成为0,1,2,3,4,5,6,7;其对应关系分别与星座图映射时相同。再经过L-2电平转换和串并变换就可以得到输出数据序列。其原理如图2所示。
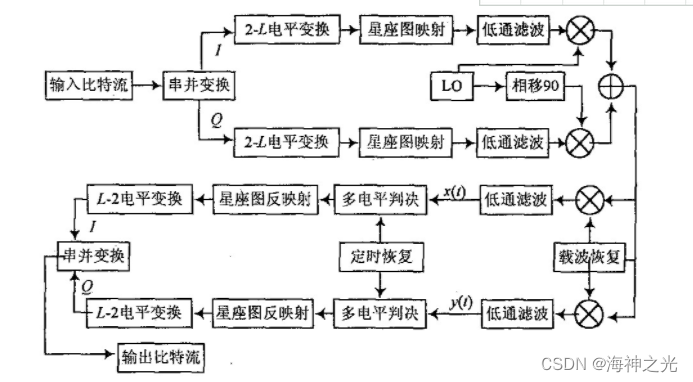
在这里插入图片描述
图2 16QAM(L=4),64QAM(L=6) 调制解调的原理框图

(1)16QAM之所以以±2,±0.5而非±2,0为判决电平,是因为在调制解调过程会产生延迟,使解调后在最初的时候产生直流,经判决后为0,这也是在看解调后的星座图时,最初会在原点处有点出现,一会又消失的原因;以16QAM ,32QAM为例,其星座图见图1的16QAM解调后初始星座图。若以±2,0为判决电平,则将会将延迟产生的直流误判为+1或-1。32QAM,64QAM,128QAM与16QAM在这一点上相同。

(2)调制信号经信道传输过程会有能量损耗,所以在解调时应加必要的增益(下同)。

⛄二、部分源代码

clear all;
close all;
clc;
%参量定义
MES_LEN=4*10000; % source message length
SYM_LEN=MES_LEN/4;% symbol length
INSERT_TIMES=8; %insert times befor filter
PETAL=5; %num of petals each side of filter
BETA=0.5; %filter bandwidth
SELECT=2; %mode slect

switch SELECT
case 1,%模式1:单个SNR下的调制、解调、误码分析
SNR=12;%符号SNR值
%产生调制信号
[signal_sendI,signal_sendQ,message,signal_base_band]=Modulation(MES_LEN,SYM_LEN,INSERT_TIMES,PETAL,BETA);
%加高斯白噪声
[signal_receiveI,signal_receiveQ]=AddNoise(signal_sendI,signal_sendQ,SNR,INSERT_TIMES);
%接收机解调
[mymessage,mysignal_base_band]=Receiver(signal_receiveI,signal_receiveQ,INSERT_TIMES,MES_LEN,SYM_LEN,BETA,PETAL);
%误码率统计
ErrBit = MES_LEN-sum((mymessage == message));
ErrSym = SYM_LEN-sum((mysignal_base_band == signal_base_band));
MyErrBitRate=ErrBit/MES_LEN;
MyErrSymRate=ErrSym/SYM_LEN;
%理论误符号率公式
TherSer=SER_16QAM(SNR);
case 2,%模式2：误码曲线的绘制
SNR = [10 12 14 16 18 20]; %符号SNR值
SumBit = zeros(1,length(SNR));
SumErrBit = zeros(1,length(SNR));
SumSym = zeros(1,length(SNR));
SumErrSym = zeros(1,length(SNR));
h=waitbar(0,'正在绘制，请稍候 …… ‘);
for k = 1:length(SNR)
SumSym(1,k) = 0;
SumErrSym(1,k) = 0;
SumBit(1,k) =0;
SumErrBit(1,k) =0;
while(SumErrSym(1,k)<100 && SumSym(1,k)<SYM_LEN50) %出现100个误符号或者仿真点数太多时停止
%产生调制信号
[signal_sendI,signal_sendQ,message,signal_base_band]=Modulation(MES_LEN,SYM_LEN,INSERT_TIMES,PETAL,BETA);
close all;
%加高斯白噪声
[signal_receiveI,signal_receiveQ]=AddNoise(signal_sendI,signal_sendQ,SNR(k),INSERT_TIMES);
close all;
%接收机解调
[mymessage,mysignal_base_band]=Receiver(signal_receiveI,signal_receiveQ,INSERT_TIMES,MES_LEN,SYM_LEN,BETA,PETAL);
close all;
%误码率统计
ErrBit = MES_LEN-sum((mymessage == message));
ErrSym = SYM_LEN-sum((mysignal_base_band == signal_base_band));
SumErrBit(1,k) = SumErrBit(1,k) + ErrBit;
SumErrSym(1,k) = SumErrSym(1,k) + ErrSym;
SumBit(1,k) = SumBit(1,k) +MES_LEN;
SumSym(1,k) = SumSym(1,k) +SYM_LEN;
end
waitbar(k/length(SNR),h);
end
close(h);
MyErrBitRate = SumErrBit./SumBit %仿真得到的误比特率
MyErrSymRate = SumErrSym./SumSym %仿真得到的误符号率
TherSer=SER_16QAM(SNR); %理论误符号率
%绘制误符号率和误比特率曲线
figure;
semilogy(SNR, MyErrSymRate, 'b-’);
hold on;
semilogy(SNR, MyErrBitRate, ‘r-.’);
hold on;
semilogy(SNR, TherSer, ‘r-*’);

        legend('仿真误符号率','仿真误比特率','理论误符号率');
        xlabel('符号信噪比 /dB');
        ylabel('错误概率');
        grid on;

end

⛄三、运行结果

在这里插入图片描述

⛄四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 于风云,张平.QAM调制与解调的全数字实现[J].现代电子技术. 2005,(03)