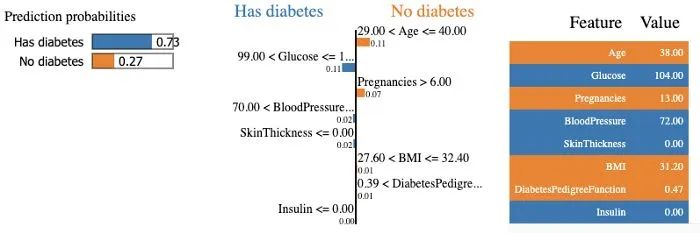
目录
- 简介
- 不可分离型分布
- 不可分离型切比雪夫
- 圆口径泰勒综合
- 可分离型分布
- 可分离切比雪夫综合
- 可分离泰勒综合
- 平面阵列配相抵消法
简介
按行、列排列的可分离型矩形平面阵,其阵因子是两个正交排列的直线阵阵因子的乘积。可分离的平面阵方向图在两个主面内是满足预期副瓣电平的,而在其他剖面内的方向图副瓣电平非常低。在各个剖面内的副瓣电平都相等或者接近的分布方式包括不可分离切比雪夫和圆口径泰勒分布等。
不可分离型分布
不可分离型切比雪夫
采用不可分离型切比雪夫激励分布设计的矩形平面阵列,限制条件是矩形阵列的每行和每列的单元数相同,但不一定是方阵,因为两个正交方向的单元间距xd和yd可不一定相等。不可分离切比雪夫激励分布设计的矩形平面阵列,其通过最大值的任意剖面内的方向图副瓣电平均相等。
不可分离切比雪夫分布对应的单元激励如下所示:


一个1616阵元的不可分离型切比雪夫分布如下所示:

一个1616阵元的不可分离型切比雪夫分布的平面阵的方向图如下所示:

圆口径泰勒综合
圆口径泰勒综合方法是由圆口径上的连续电流面源出发,综合得到其连续面源分布,然后根据抽样定理,可得到离散的圆口径阵列单元的幅度分布。这种阵列口径分布即使是矩形栅格构成的圆形阵,也是不能按行列分离的,属于不可分离型分布。采用圆口径泰勒综合方法得到的圆口径分布能满足各个剖面都是低副瓣的要求。
圆口径泰勒分布的阵列因子如下所示:

一个直径16单元的圆口径的泰勒分布如下所示:

直径16单元的圆口径的泰勒分布对应的方向图如下所示:

可分离型分布
可分离型矩形平面阵按列的激励分布为 Ixm,按行的激励分布为 Iyn,则第(m,n)个单元的激励为 Imn= Ixmx Iyn。其阵因子是两个正交排列的直线阵阵因子的乘积。对这类阵列的综合,可按行、列排列的两个直线阵分别进行综合。得到的平面阵方向图在两个主面内是满足预期副瓣电平的,而在其他剖面内,其方向图副瓣电平非常低。
可分离切比雪夫综合
对于可分离型切比雪夫平面阵,它所产生的方向图为两个正交排列的直线阵方向图的乘积。这种平面阵的设计是较简单的,只需要由两个主面方向图的指标(主瓣宽度、副瓣电平),分别设计沿 x 和 y 轴两个方向排列的直线阵即可。一个16*16阵元的平面可分离的切比雪夫分布如下所示:

对应的方向图如下所示:

可分离泰勒综合
对于可分离型泰勒平面阵,它所产生的方向图为两个正交排列的直线阵方向图的乘积。一个1616阵元的平面可分离的泰勒分布如下所示:

1616阵元的平面可分离的泰勒分布的方向图如下所示:

平面阵列配相抵消法
这种方法是对阵列若干个单元进行“0、π配相”使得阵列天线在副瓣方向上这些单元的辐射场相互抵消,从而实现降低副瓣电平的目的。
一个1616的平面阵列,馈电激励均为1,相位分布如下所示(其中黄色为180度相位,蓝色为0度相位):

一个1616的平面阵列进行配相法综合得到的方向图如下所示: