题目链接

Leetcode.1992 找到所有的农场组 Rating ： 1539

题目描述

给你一个下标从 0 开始，大小为 m x n 的二进制矩阵 land ，其中 0 表示一单位的森林土地，1 表示一单位的农场土地。

为了让农场保持有序，农场土地之间以矩形的 农场组 的形式存在。每一个农场组都 仅 包含农场土地。且题目保证不会有两个农场组相邻，也就是说一个农场组中的任何一块土地都 不会 与另一个农场组的任何一块土地在四个方向上相邻。

land 可以用坐标系统表示，其中 land 左上角坐标为 (0, 0) ，右下角坐标为 (m-1, n-1) 。请你找到所有 农场组 最左上角和最右下角的坐标。一个左上角坐标为 (r1, c1) 且右下角坐标为 (r2, c2) 的 农场组 用长度为 4 的数组 [r1, c1, r2, c2] 表示。

请你返回一个二维数组，它包含若干个长度为 4 的子数组，每个子数组表示 land 中的一个 农场组 。如果没有任何农场组，请你返回一个空数组。可以以 任意顺序 返回所有农场组。

示例 1：

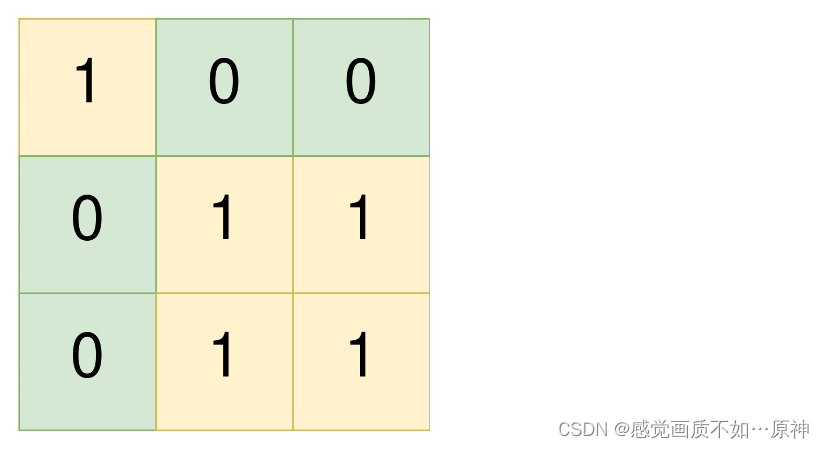
输入：land = [[1,0,0],[0,1,1],[0,1,1]]
输出：[[0,0,0,0],[1,1,2,2]]
解释：
第一个农场组的左上角为 land[0][0] ，右下角为 land[0][0] 。
第二个农场组的左上角为 land[1][1] ，右下角为 land[2][2] 。

示例 2：

输入：land = [[1,1],[1,1]]
输出：[[0,0,1,1]]
解释：
第一个农场组左上角为 land[0][0] ，右下角为 land[1][1] 。

示例 3：

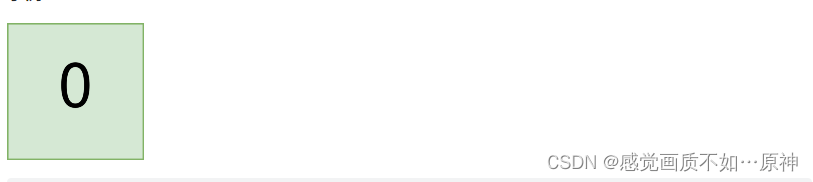
输入：land = [[0]]
输出：[]
解释：
没有任何农场组。

提示：

• $m==land.length$
• $n==land[i].length$
• $1<=m,n<=300$
• land只包含 0 和 1 。
• 农场组都是 矩形 的形状。

解法：dfs

我们在 dfs 遍历 农场组 （全为 1 的位置 ）时，需要记录这个农场组的 左上节点 $(x1,y1)$ 和 右下节点$(x2,y2)$。

由于我们是从左上角开始遍历的，所以 左上节点 $(x1,y1)$ 最开始就确定了。

所以我们每次只需要更新 右下节点$(x2,y2)$ 即可。

时间复杂度： $O(mn)$

C++代码；

const int dx[4] = {1,0,-1,0};
const int dy[4] = {0,1,0,-1};
class Solution {
public:
    vector<vector<int>> findFarmland(vector<vector<int>>& g) {
        int m = g.size() , n = g[0].size();

        bool st[m][n];
        memset(st,false,sizeof st);

        function<void(int,int,int&,int&)> dfs = [&](int i,int j,int& x2,int& y2) ->void{
            if(i < 0 || i >= m || j < 0 || j >= n || g[i][j] == 0 || st[i][j]) return;
            
            st[i][j] = true;

            if(i > x2 || j > y2){
                x2 = i, y2 = j;
            }

            for(int k = 0;k < 4;k++){
                dfs(i + dx[k] , j + dy[k],x2,y2);
            }
        };

        vector<vector<int>> ans;
        for(int i = 0;i < m;i++){
            for(int j = 0;j < n;j++){
                if(g[i][j] && !st[i][j]){
                    int x1 = i , y1 = j , x2 = i, y2 = j;
                    dfs(i,j,x2,y2);
                    ans.push_back({x1,y1,x2,y2});
                }
            }
        }

        return ans;
    }
};