实例3：汉诺塔

汉诺塔是一个可以使用递归解决的经典问题，它源于印度一个古老传说：大梵天创造世界的时候做了三根金刚石柱子，其中一根柱子从下往上按照从大到小的顺序摞着64片黄金圆盘，大梵天命令婆罗门把圆盘从下面开始按照从大到小的顺序重新摆放在另一根柱子上，并规定：小圆盘上不能放大圆盘，三根柱子之间一次只能移动一个圆盘。问一共需要移动多少次，才能按照要求移完这些圆盘。三根金刚柱子与圆盘摆放方式如图1所示。

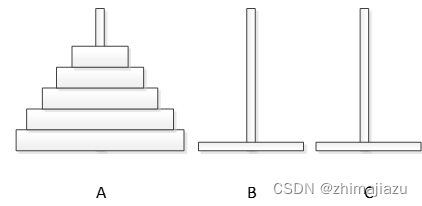
图1 汉诺塔格局图

本实例要求编写程序，实现输出汉诺塔移动过程的功能。

实例目标

明确递归函数的递归公式与边界条件
熟练地定义递归函数

实例分析

我们先来分析一下移动n个圆盘的过程：

（1）假设现在A柱子上只有1个圆盘，此时无需B柱子中转而直接将圆盘从A柱子移动到C柱子上。

（2）假设A柱子上有2个圆盘，此时可以先将小盘子移动到B柱子上，再将大盘子移动到C柱子上，最后将小盘子移动到C柱子上。我们既可以借助柱子B将2个盘子从A移动到C，也可以借助C将2个盘子从A移动到B。

（3）假设A柱子上有3个圆盘，则可以根据移动2个盘子的过程，先借助柱子C将柱子A上的两个盘子先移动到柱子B，将A上的大盘子移动到柱子C上，此时A成为空柱子，再借助柱子A，将柱子B上两个盘子移动到C。

（4）以此类推，假设A柱子上有n个盘子，则可以将n-1个盘子看作一个整体，也就是递归中的子问题。例如，借助柱子C先将柱子A上的n-1个盘子移动到柱子B上，再将柱子A上最大的盘子移动到柱子C上，此时A成为空柱子，最后借助柱子A，将柱子B上n-2个盘子移动到柱子A上，将柱子B上最大的盘子移动到柱子C上，此时B成为空柱子......如此往复。

经过上述分析的过程，递归函数边界条件和递归公式分别如下：

（1）边界条件：当n为1时，直接将盘子从A移动到C；

（2）递归公式：当n为n时，直接将n-1个盘子先从A移动到空柱子B上，再将第n个盘子移动到柱子C上，最后将柱子B上的n-1个盘子移动到柱子C上。

代码实现

def hanoi(n, ch1, ch2, ch3):

if n == 1:

print(ch1, '->', ch3)

else:

hanoi(n - 1, ch1, ch3, ch2)

print(ch1, '->', ch3)

hanoi(n - 1, ch2, ch1, ch3)

plate_nums = int(input("请输入盘子的数量："))

hanoi(plate_nums, 'A', 'B', 'C')

以上代码首先定义了一个递归函数hanoi()，该函数包含n、 ch1、ch2、ch3共4个参数，其中参数n表示用户输入的盘子数量，ch1、ch2、ch3分别表示柱子A、B、C的名称，该函数中分别处理了1个盘子和n-1个盘子的情况，然后接收用户输入的盘子数量plate_nums，最后调用hanoi()函数输出plate_nums个盘子的移动过程。