快慢指针

代码思路：

slow 和fast 指向 head slow走一步，fast走两步

没有环：

fast每次走2步，如果 fast 最终遇到NULL(链表中的元素是偶数)或者fast->next(链表中的元素是奇数)遇到NULL，说明链表中没有环

在这里插入图片描述

有环：

如果 fast 和 slow指针在途中相遇，说明这个链表有环

因为fast 比slow 走的快，如果 fast 最终和 slow 相遇，那肯定是 fast 超过了 slow 一圈，说明链表中含有环。

bool hasCycle(struct ListNode *head)
 {
        struct ListNode * slow =head , * fast = head ;

   //假设带环
    while ( fast!= NULL && fast->next != NULL)
    { 
       fast =fast->next->next ;
       slow = slow->next ;
       if( slow  == fast )  //因为fast每次走2步 ，slow每次走一步 如果有环 那一定是fast追上slow 也就是相遇
       {
           return true ;
       }
    }
     //fast 为NULL 或者 fast->next 为NULL    如果 fast 最终遇到空指针，说明链表中没有环 
     return false ; 
}

我们证明一下这个逻辑问题：

为什么 slow 走一步 fast 走两步 ,fast 和slow 会相遇 ,有没有可能会错过

假设slow 刚开始进环的时候 slow 和fast 的距离是N ，slow开始进环的时候 fast开始追及slow ,因为fast 每次走两步，而slow 每次走一步 ,也就是说在追及的过程中 fast 与slow每次缩短一步的距离
不管N 是否为奇数还是偶数 , N每次减一，迟早为0 ，也就意味着fast 追上了 slow

在这里插入图片描述

那我们再推广一下

如果slow 走一步 ,fast 走 X 步（ X >=3) ，fast 和slow 会相遇？或者有可能错过?
假设slow刚开始进环，fast 和slow 的距离是N
slow进环以后 fast 开始追及slow ,slow每次走一步 ,fast 就走三步 ,距离缩小 2 步
如果N 是偶数 N -2 ， N-4 ， N - 6 ， 4 ， 2 …N可以减到零
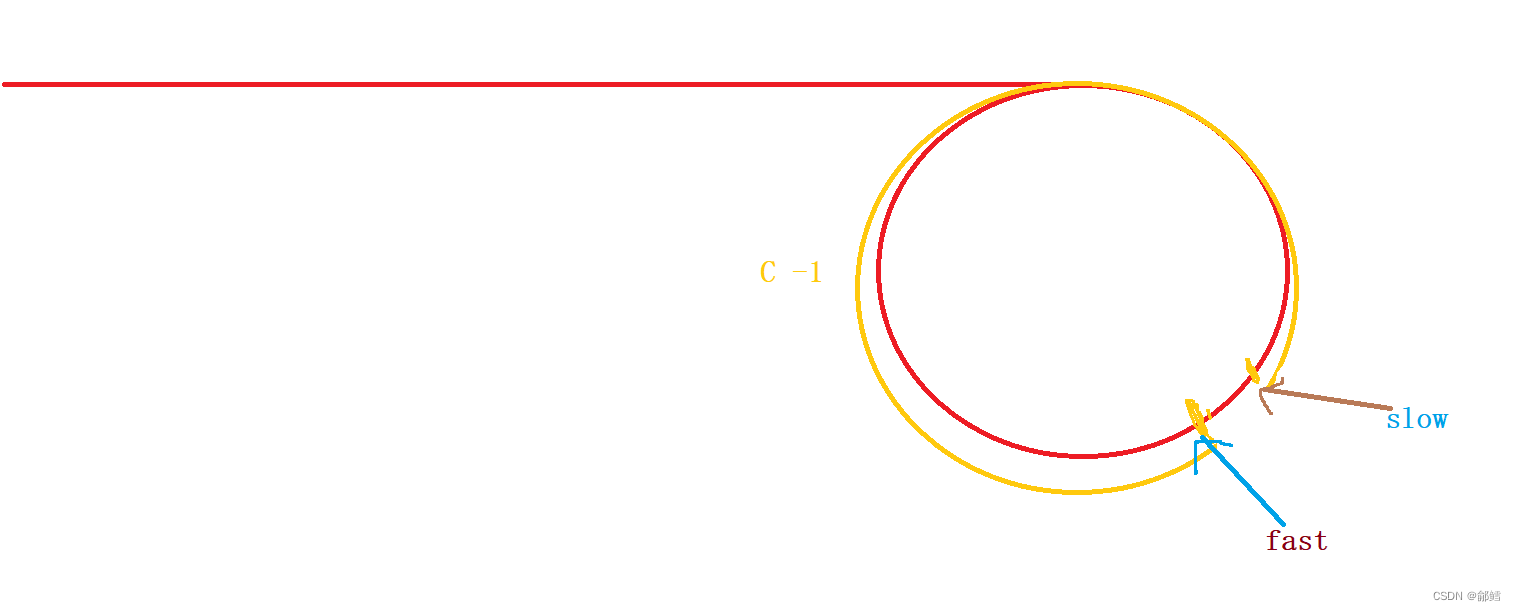
如果N 是奇数 N -2 ， N-4 ， … 3 ,1, -1
我们假设环的周长是C ，N 是 -1 ，也就是说 fast 和slow 的距离变成了 C-1 ，又开始了新的一轮追及

在这里插入图片描述

142.环形链表II

结论：一个指针(fast)从相遇点开始走，一个指针(slow)从起始点开始走，会在入口点相遇

结论千万不要理解为slow 去追fast 了 ,其实是fast追slow ,只不过fast走的快，可能在环里转了n 圈
一旦slow走到入口点，fast 就会和slow 相遇

下面我们来证明一下上述结论：
假设起始点到入口点处的距离是L ，入口点处到相遇点的距离为X
环的长度为C

那么可以推出slow 走的距离为L + X ,
fast 走的距离是 L+ n* C + X ,
n* C 表示 slow 进环前，fast 在环里转了n*C 圈

根据fast 走的距离是slow 的两倍
2（L+X ) = L + n *C + X
推出 L= n * C -X

将这个推导式变形得到 L = （ n -1) * C + C -X
即证明结论成立

struct ListNode *detectCycle(struct ListNode *head)
 {
     struct ListNode * fast = head , * slow = head ;
      
      // 假设带环
      while ( fast != NULL && fast->next!=NULL)
      {
          slow =slow->next ;
          fast =fast->next->next ;
             if( slow == fast )  
             {
                  struct ListNode * meet = fast  ;  //相遇点
                   struct ListNode * start = head ;//起始点
                   while( meet!= start ) // 一个指针(fast)从相遇点开始走 ，一个指针(slow)从起始点开始走 ，会在入口点相遇
                   {
              meet= meet->next ;
              start=start->next ;
                   }
                   return meet ;

             }
      }
       return NULL ; //不带环
    
}