一、不同进制的表示方式

所有数字在计算机底层都以二进制形式存在
对于整数，有四种表示方式
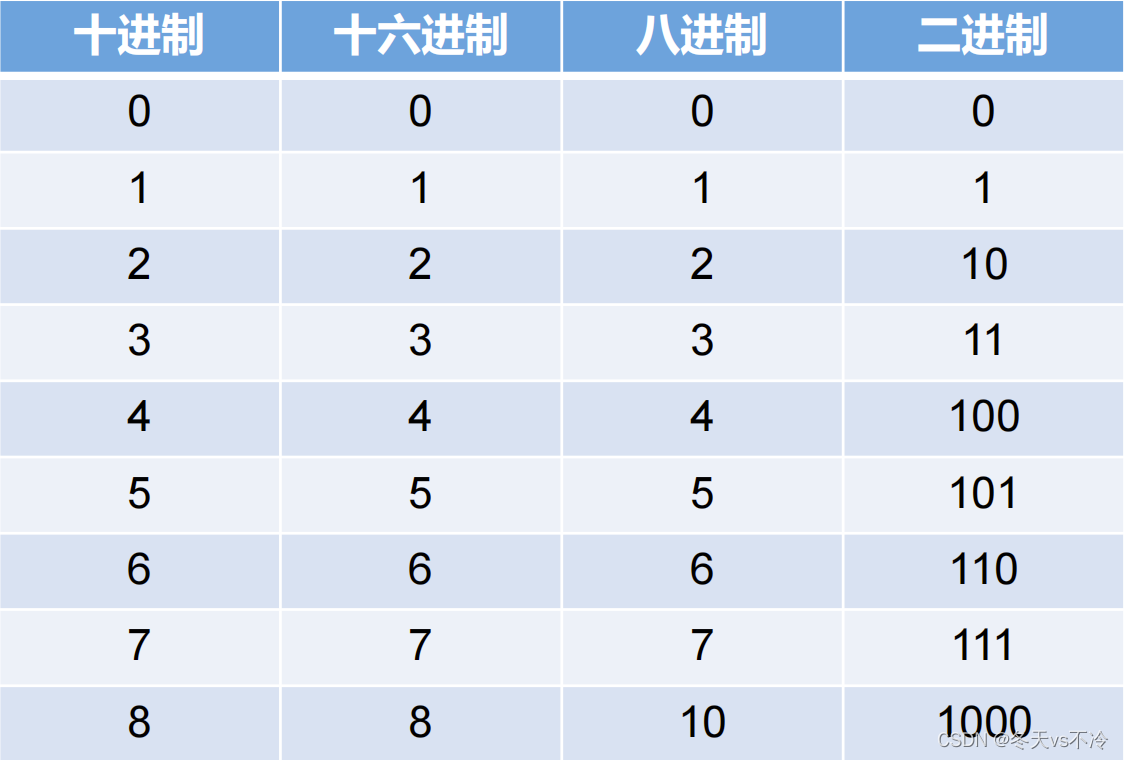
- 二进制(binary)：0,1 ，满2进1，以0b或0B开头
- 十进制(decimal)：0-9 ，满10进1
- 八进制(octal)：0-7 ，满8进1，以数字0开头表示
- 十六进制(hex)：0-9及A-F，满16进1，以0x或0X开头表示。此处的A-F不区分大小写。如：0x21AF +1= 0X21B0

在这里插入图片描述

二、二进制

Java整数常量默认是int类型，当用二进制定义整数时，其第32位是符号位；当是long类型时，二进制默认占64位，第64位是符号位
二进制的整数有如下三种形式
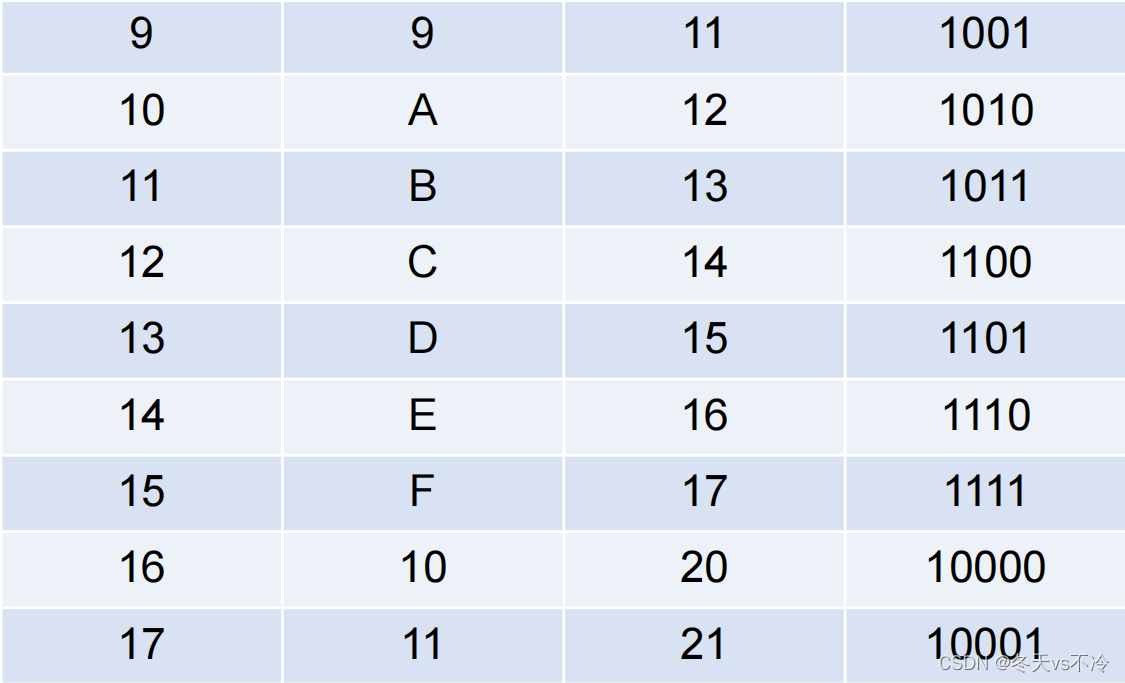
- 原码：直接将一个数值换成二进制数。最高位是符号位
- 负数的反码：是对原码按位取反，只是最高位（符号位）确定为1
- 负数的补码：其反码加1。计算机以二进制补码的形式保存所有的整数
- 正数的原码、反码、补码都相同，负数的补码是其反码+1

为什么要使用原码、反码、补码表示形式呢？

计算机底层都是使用补码进行存储和计算（正数不变，负数补码是其反码+1）
主要要解决的问题就是负数的表示
1. 假设我们有正数0000 1111，我们如何表示其相反数呢？
2. 一般我们的思路是，找一个数，跟它相加的结果等于0，但是我们发现，要找出一个与它相加后结果等于0的数还是要略加思考一下的(因为要计算进位)
3. 所以，为何不找出一个与它相加后结果是1111 1111的数，然后该数+1即是我们所要的答案啦
4. 于是，很容易的，0000 1111 + 1111 0000 + 1 = 1111 1111 1111 1111 + 1 = (1)0000 0000 （超过最高位数的1舍去）
5. 一目了然，1111 0001 就是我们想要的答案了
6. 那么我们是怎么得到这个相反数的呢？
  - 首先，找出一个数与它加起来结果是全1的，这个数便是它的反码
  - 然后这个数再加1，这便是它的相反数了，也是我们说的补码
  - 我们检验一下0的情况，0000 + 1111 + 1 =(1)0000，其中1111 + 1 = (1)0000 = 0000，即+0和-0的二进制表示均为0000

三、进制之间的转换

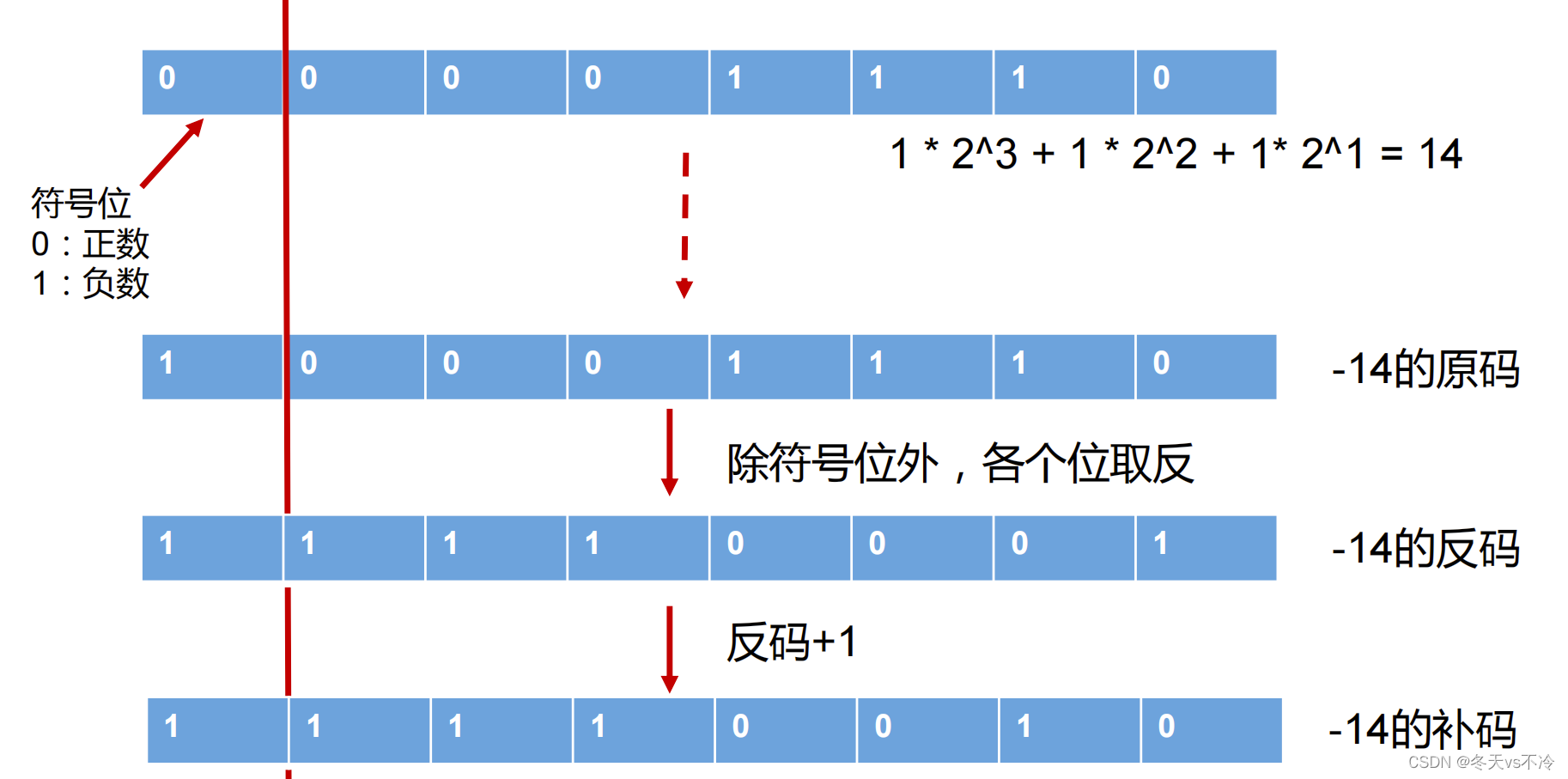
二进制转十进制

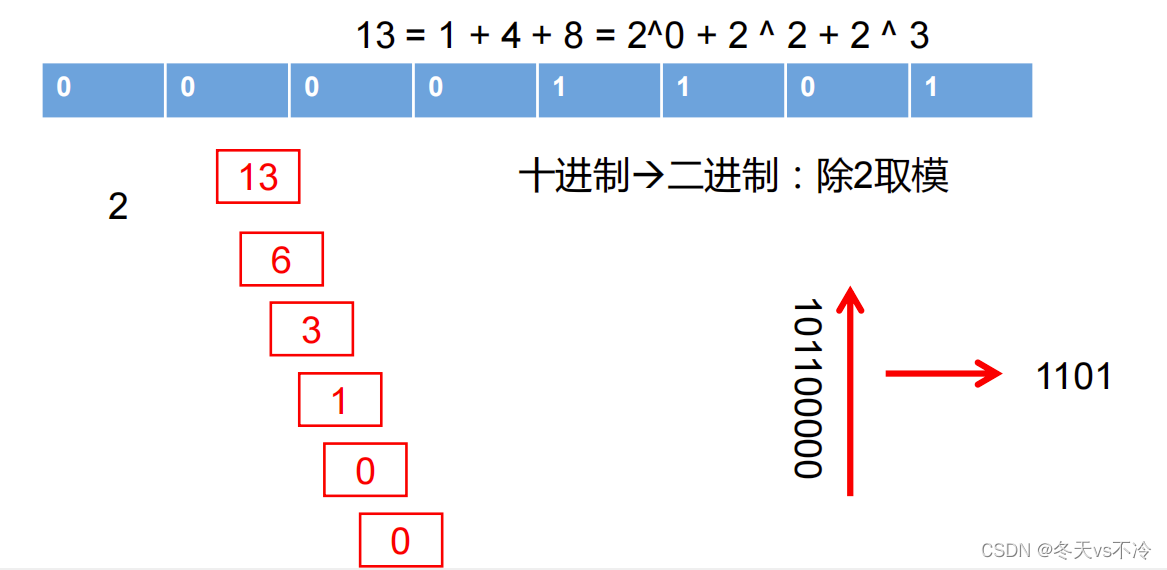
在这里插入图片描述

十进制转二进制

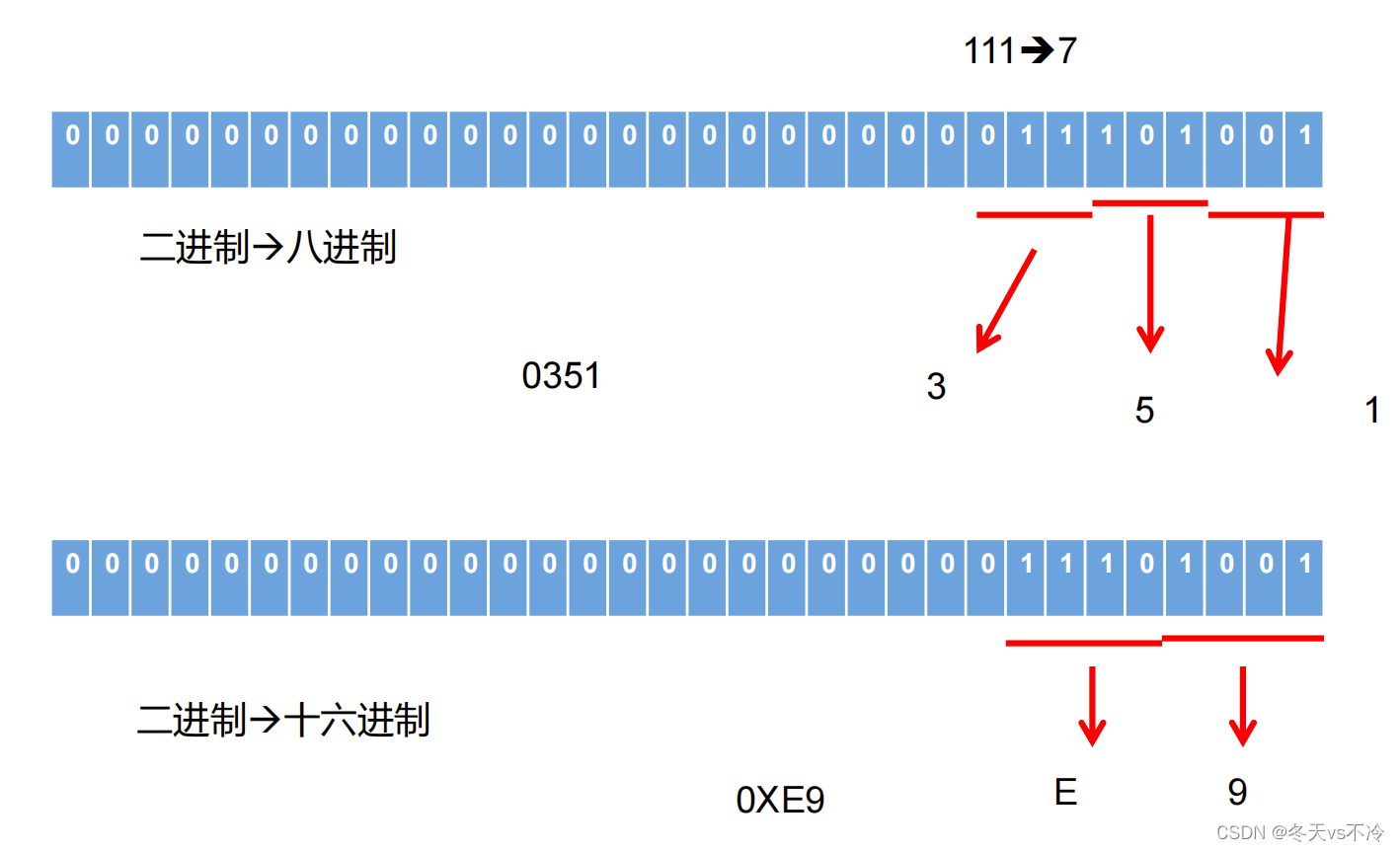
在这里插入图片描述

二进制与八进制转换

在这里插入图片描述

四、byte的取值范围

byte 在计算机中是8位；第一位为符号位。0表示正数，1表示为负数，其余的7位表示具体的值
数值在计算机内存中的存储是补码的方式
正数最大为0111 1111，十进制表示形式为127
-0的原码是1000 0000，反码是 1111 1111，补码是 10000 0000 ，因为byte只识别8位字节，所以补码是 0000 0000
+0的原码是 0000 0000 ，反码补码都是其本身，还是0000 0000
对于0来说，底层存储补码，就只有0000 0000，把-0和+0都包括了

原码 -1 是  1000 0001 ，   -127是 1111 1111

反码    是  1111 1110 ，       是 1000 0000

补码    是  1111 1111 ，       是 1000 0001
    
即补码 1111 1111 到补码 1000 0001 表示 -1 到 -127