堆的结构与实现
- 二叉树的顺序结构
- 堆的概念及结构
- 堆的实现
- 堆的创建
- 向上调整建堆
- 向下调整建堆
- 堆的操作链接
二叉树的顺序结构
堆其实是具有一定规则限制的完全二叉树。
普通的二叉树是不太适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树会更适合使用顺序结构进行存储。如下图:
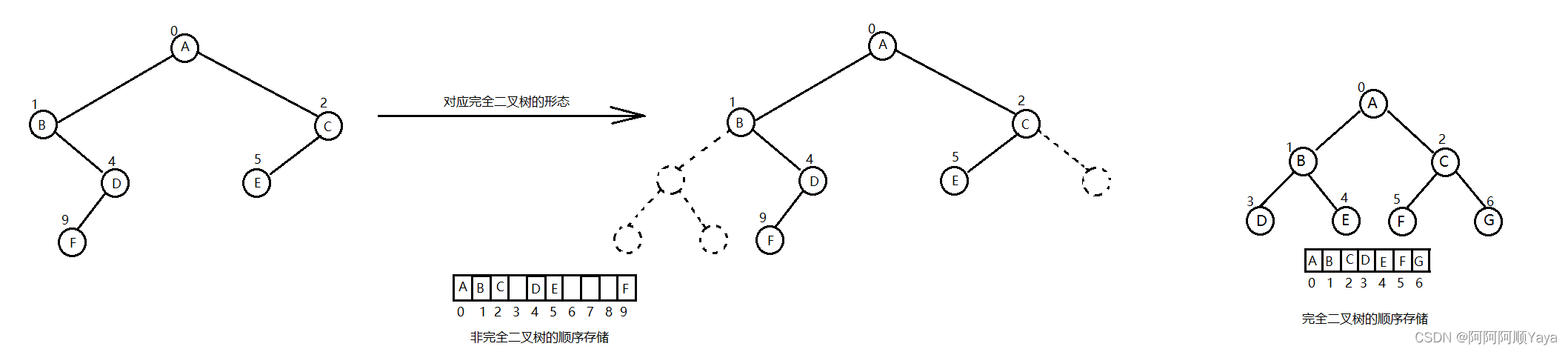
堆的概念及结构
如果有一个关键码的集合
K
=
{
k
0
,
k
1
,
k
2
,
.
.
.
,
k
n
−
1
}
K=\{k_0, k_1, k_2, ..., k_{n-1}\}
K={k0,k1,k2,...,kn−1},当把它的所有元素按完全二叉树的顺序存储方式存储在一个一维数组中,并且满足:
K
i
≤
K
2
∗
i
+
1
K_i\leq K_{2*i+1}
Ki≤K2∗i+1且
K
i
≤
K
2
∗
i
+
2
K_i\leq K_{2*i+2}
Ki≤K2∗i+2(
K
i
≥
K
2
∗
i
+
1
K_i\ge K_{2*i+1}
Ki≥K2∗i+1且
K
i
≥
K
2
∗
i
+
2
K_i\ge K_{2*i+2}
Ki≥K2∗i+2),i=0, 1, 2, …,则称之为小堆(大堆)。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
堆的性质:
- 堆中某个节点的值总是不大于或不小于其父节点的值
- 堆总是一棵完全二叉树。

堆的实现
堆的创建
下面给出一个数组,这个数组逻辑上可以看做一棵完全二叉树,但是还不满足堆的条件。现在我们可以通过算法,将它构建成一个堆。
int a[] = {27,15,19,18,28,34,65,49,25,37};
要将其构建成一个堆结构,有两种调整建堆的方法:一种是向上调整建堆,一种是向下调整建堆。
向上调整建堆
向上调整建堆主要是用于在堆数据结构中,堆在插入数据后,为了继续维持堆的结构,所进行的一种调整。
大致调整过程如下:
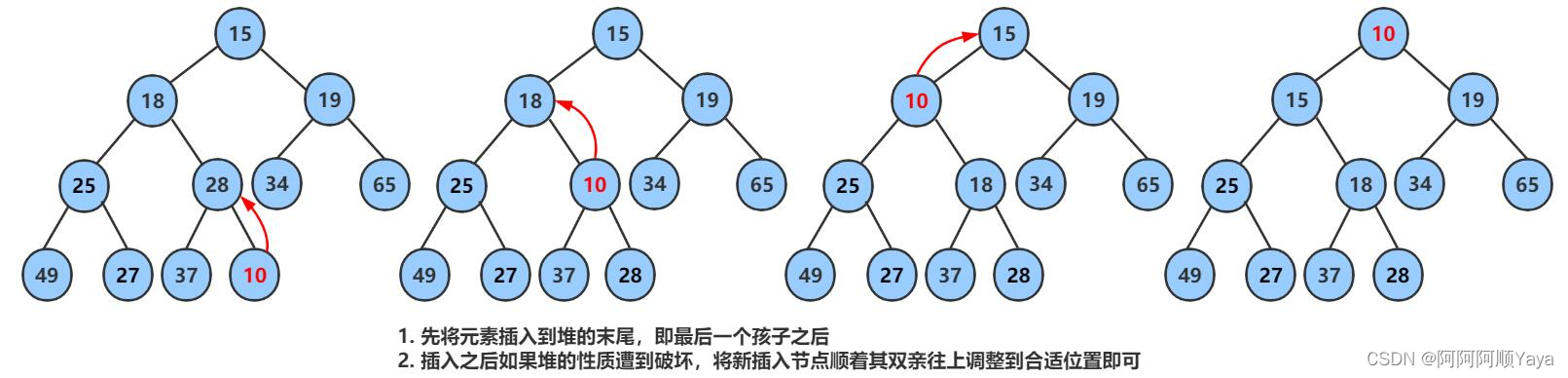
经过一次向上调整后,本来因为插入数据所导致的堆的结构的破坏就被恢复了。
有了这个思路,可以将过程实现如下:
//a - 堆的顺序存储数组
//child - 需要进行向上调整的孩子下标
void AdjustUp(HDataType* a, int child)
{
assert(a != NULL);
int parent = (child - 1) / 2;
while (child > 0)//child为0时,child就到了堆顶,调整结束
{
//建小堆 - 孩子比双亲小,就互换位置
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);//交换函数
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
以上只是对一个数据进行的调整,要想实现堆的创建,需要将数组中的所有数据都进行一遍调整(堆顶元素除外),所以可以更进一步,完成一棵完全二叉树到堆的创建。
for (int i = 1; i < n; ++i)
{
AdjustUp(a, i);
}
以上就是向上调整建堆的过程,我们可以分析一下它的时间复杂度。
因为堆是完全二叉树,而满二叉树也是完全二叉树,此处为了简化,使用满二叉树来证明。(时间复杂度看的本来就是近似值,多几个节点并不影响最终结果)
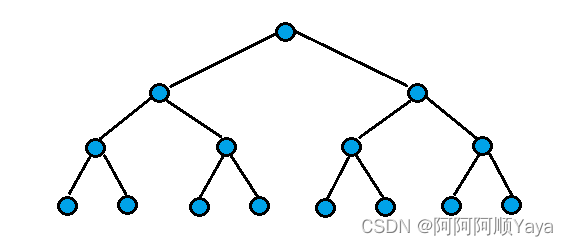
假设树的高度为h
第1层, 2 0 2^0 20个节点,需要向上调整0层。
第2层, 2 1 2^1 21个节点,需要向上调整1层。
第3层, 2 2 2^2 22个节点,需要向上调整2层。
第4层, 2 3 2^3 23个节点,需要向上调整3层。
…
第h-1层, 2 h − 2 2^{h-2} 2h−2个节点,需要向上调整h-2层。
第h层, 2 h − 1 2^{h-1} 2h−1个节点,需要向上调整h-1层。
则需要移动节点总的移动步数为:
T
(
n
)
=
2
0
∗
0
+
2
1
∗
1
+
2
2
∗
2
+
2
3
∗
3
+
.
.
.
.
.
.
+
2
(
h
−
2
)
∗
(
h
−
2
)
+
2
(
h
−
1
)
∗
(
h
−
1
)
T(n)=2^0*0+2^1*1+2^2*2+2^3*3+......+2^{(h-2)}*(h-2)+2^{(h-1)}*(h-1)
T(n)=20∗0+21∗1+22∗2+23∗3+......+2(h−2)∗(h−2)+2(h−1)∗(h−1)
2
T
(
n
)
=
2
1
∗
0
+
2
2
∗
1
+
2
3
∗
2
+
2
4
+
3
+
.
.
.
.
.
.
+
2
(
h
−
1
)
∗
(
h
−
2
)
+
2
h
∗
(
h
−
1
)
2T(n)=2^1*0+2^2*1+2^3*2+2^4+3+......+2^{(h-1)}*(h-2)+2^h*(h-1)
2T(n)=21∗0+22∗1+23∗2+24+3+......+2(h−1)∗(h−2)+2h∗(h−1)
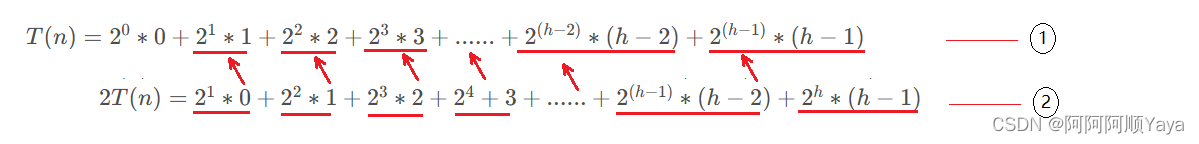
由错位相减得:
T
(
n
)
=
−
2
0
−
2
1
−
2
2
−
2
3
−
2
4
−
2
(
h
−
2
)
−
2
(
h
−
1
)
+
2
h
∗
(
h
−
1
)
T(n)=-2^0-2^1-2^2-2^3-2^4-2^{(h-2)}-2^{(h-1)}+2^h*(h-1)
T(n)=−20−21−22−23−24−2(h−2)−2(h−1)+2h∗(h−1)
T
(
n
)
=
2
h
∗
(
h
−
1
)
−
(
2
0
+
2
1
+
2
2
+
2
3
+
2
4
+
2
(
h
−
2
)
+
2
(
h
−
1
)
)
T(n)=2^h*(h-1)-(2^0+2^1+2^2+2^3+2^4+2^{(h-2)}+2^{(h-1)})
T(n)=2h∗(h−1)−(20+21+22+23+24+2(h−2)+2(h−1))
T
(
n
)
=
2
h
∗
(
h
−
1
)
−
(
2
h
−
1
)
=
2
h
∗
(
h
−
2
)
+
1
T(n)=2^h*(h-1)-(2^h-1)=2^h*(h-2)+1
T(n)=2h∗(h−1)−(2h−1)=2h∗(h−2)+1
因为是满二叉树,所以节点数n与高度h之间存在如下关系:
n
=
2
h
−
1
n=2^h-1
n=2h−1,
h
=
l
o
g
2
(
n
+
1
)
h=log_2(n+1)
h=log2(n+1)
所以
T
(
n
)
=
(
n
+
1
)
∗
(
l
o
g
2
(
n
+
1
)
−
2
)
+
1
T(n)=(n+1)*(log_2(n+1)-2)+1
T(n)=(n+1)∗(log2(n+1)−2)+1
因此,得出向上建堆的时间复杂度是O(
n
∗
l
o
g
2
n
n*log_2n
n∗log2n)。
向下调整建堆
堆的删除
向下调整建堆主要是用于在堆数据结构中,堆在删除数据后,为了继续维持堆的结构,所进行的一种调整。
这里要说明的是,堆的删除是指删除堆顶的数据。要删除堆顶的数据并不是像顺序表那样覆盖删除。虽然堆的物理存储结构是顺序结构,但他逻辑上是树形结构,如果直接覆盖删除,本来是兄弟节点的变成父子节点,关系会完全打乱。并不能保证最终覆盖删除之后的结构还是堆的结构。
所以,堆的删除有另一种巧妙的方法。先将堆顶的数据跟堆的最后一个数据进行交换,然后删除堆的最后一个数据,就将堆顶数据删除了。
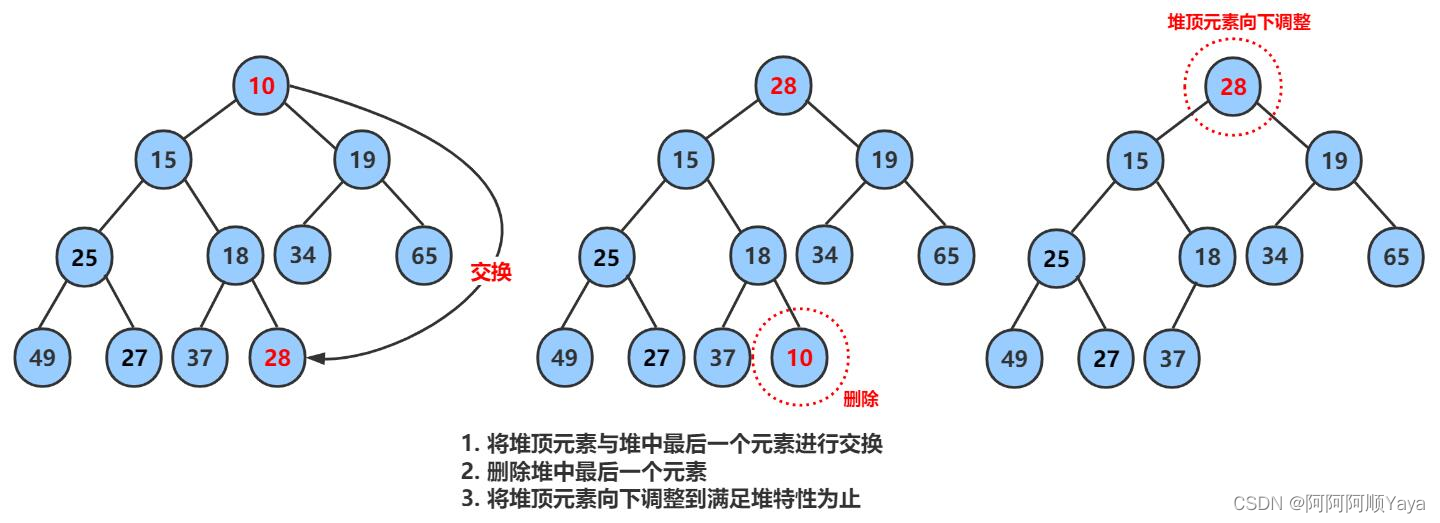
但是,堆顶的数据删除了,并没有因此就万事大吉。因为和堆顶数据进行交换的数据,现在处于堆顶位置,并不代表它就是堆中最小或最大的数据,堆的结构可能通过交换后就此被破坏。所以,这里就要通过向下调整算法来恢复堆的结构。
大致调整过程如下:
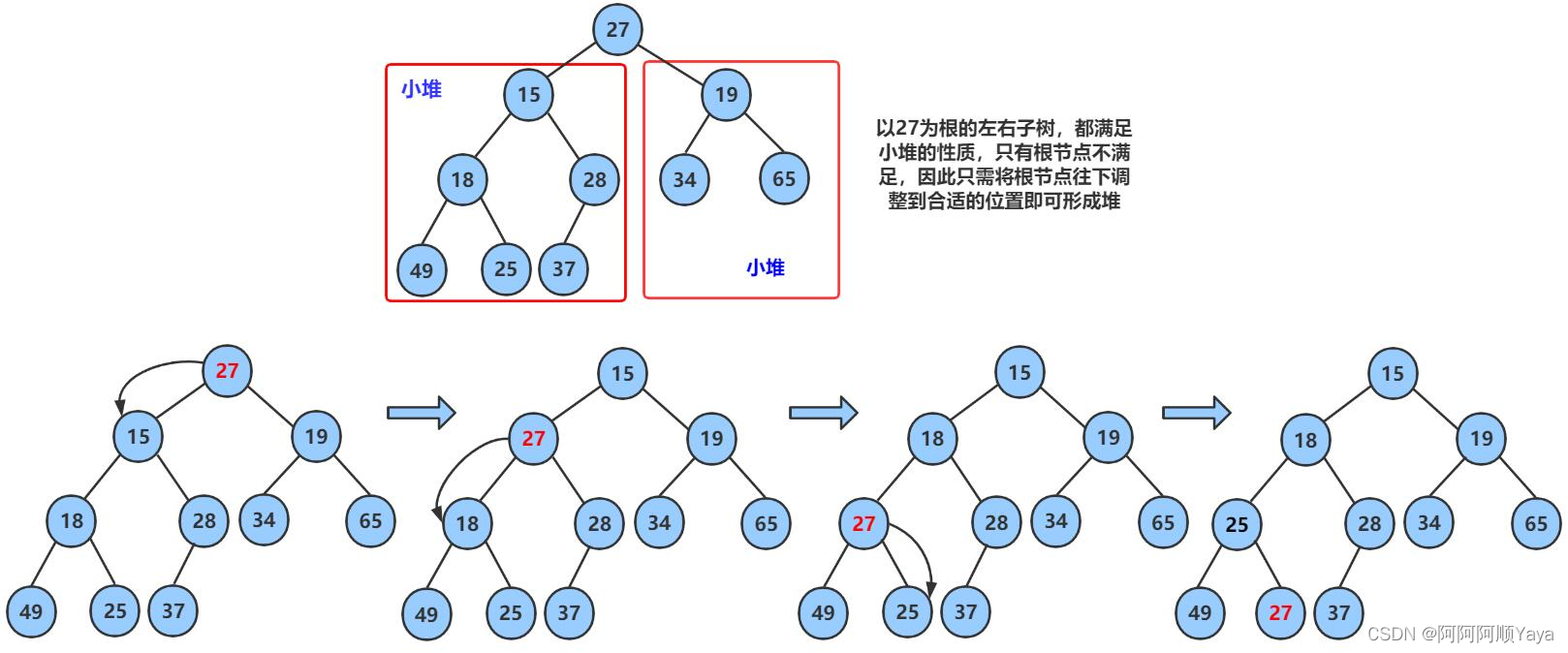
要注意的是:向下调整算法有一个前提,左右子树必须都是堆,才能调整。
经过一次向下调整后,本来因为删除数据所导致的堆的结构的破坏就被恢复了。
有了这个思路,可以将过程实现如下:
//a - 堆的顺序存储数组
//size - 堆的顺序存储数组的数据个数
//parent - 需要进行向下调整的双亲下标
void AdjustDown(HDataType* a, int size, int parent)
{
assert(a != NULL);
//此时child代表左孩子
int child = 2 * parent + 1;
//孩子下标在数组范围内进入循环
while (child < size)
{
//child+1代表右孩子
//建小堆 - 右孩子存在的话,左右孩子谁更小,child存储的就是谁的下标变量
if (child + 1 < size && a[child + 1] < a[child])
{
++child;
}
if (a[child] < a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = 2 * parent + 1;
}
else
{
break;
}
}
}
以上只是对一个数据进行的调整,要想实现堆的创建,这里我们从倒数第一个非叶子节点所形成的的子树开始调整,一直调整到根节点的树,就可以调整成堆。所以可以更进一步,完成一棵完全二叉树到堆的创建。
//n-1是最后一个数据的下标,((n-1)-1)/2是倒数第一个非叶子节点的下标
for (int i = (n - 1 - 1) / 2; i >= 0; --i)
{
AdjustDown(a, n, i);
}
以上就是向下调整建堆的过程,我们可以分析一下它的时间复杂度。
同上,采取满二叉树的结构来进行复杂度的计算。
假设树的高度为h
第1层, 2 0 2^0 20个节点,需要向下调整h-1层。
第2层, 2 1 2^1 21个节点,需要向下调整h-2层。
第3层, 2 2 2^2 22个节点,需要向下调整h-3层。
第4层, 2 3 2^3 23个节点,需要向下调整h-4层。
…
第h-1层, 2 h − 2 2^{h-2} 2h−2个节点,需要向下调整1层。
第h层, 2 h − 1 2^{h-1} 2h−1个节点,需要向下调整0层。
则需要移动节点总的移动步数为:
T
(
n
)
=
2
0
∗
(
h
−
1
)
+
2
1
∗
(
h
−
2
)
+
2
2
∗
(
h
−
3
)
+
2
3
∗
(
h
−
4
)
+
.
.
.
.
.
.
+
2
(
h
−
2
)
∗
1
+
2
(
h
−
1
)
∗
0
T(n)=2^0*(h-1)+2^1*(h-2)+2^2*(h-3)+2^3*(h-4)+......+2^{(h-2)}*1+2^{(h-1)}*0
T(n)=20∗(h−1)+21∗(h−2)+22∗(h−3)+23∗(h−4)+......+2(h−2)∗1+2(h−1)∗0
2
T
(
n
)
=
2
1
∗
(
h
−
1
)
+
2
2
∗
(
h
−
2
)
+
2
2
∗
(
h
−
3
)
+
2
4
∗
(
h
−
4
)
+
.
.
.
.
.
.
+
2
(
h
−
1
)
∗
1
+
2
h
∗
0
2T(n)=2^1*(h-1)+2^2*(h-2)+2^2*(h-3)+2^4*(h-4)+......+2^{(h-1)}*1+2^h*0
2T(n)=21∗(h−1)+22∗(h−2)+22∗(h−3)+24∗(h−4)+......+2(h−1)∗1+2h∗0
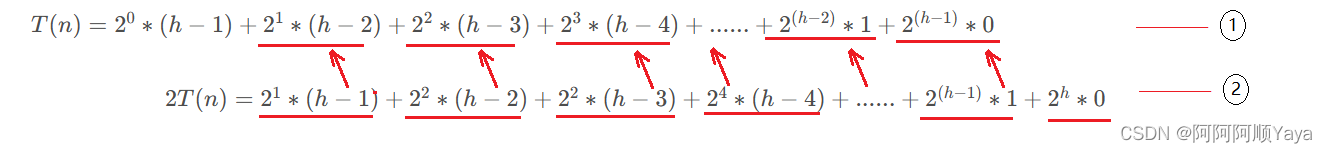
由错位相减得:
T
(
n
)
=
(
1
−
h
)
+
2
1
+
2
2
+
2
3
+
2
4
+
2
(
h
−
2
)
+
2
(
h
−
1
)
T(n)=(1-h)+2^1+2^2+2^3+2^4+2^{(h-2)}+2^{(h-1)}
T(n)=(1−h)+21+22+23+24+2(h−2)+2(h−1)
T
(
n
)
=
2
0
+
2
1
+
2
2
+
2
3
+
2
4
+
2
(
h
−
2
)
+
2
(
h
−
1
)
−
h
T(n)=2^0+2^1+2^2+2^3+2^4+2^{(h-2)}+2^{(h-1)}-h
T(n)=20+21+22+23+24+2(h−2)+2(h−1)−h
T
(
n
)
=
2
h
−
1
−
h
T(n)=2^h-1-h
T(n)=2h−1−h
因为是满二叉树,所以节点数n与高度h之间存在如下关系:
n
=
2
h
−
1
n=2^h-1
n=2h−1,
h
=
l
o
g
2
(
n
+
1
)
h=log_2(n+1)
h=log2(n+1)
所以
T
(
n
)
=
n
−
l
o
n
g
2
(
n
+
1
)
T(n)=n-long_2(n+1)
T(n)=n−long2(n+1)
因此,得出向下建堆的时间复杂度是O(n)。
通过比较,向上建堆的时间复杂度是O(
n
∗
l
o
g
2
n
n*log_2n
n∗log2n),向下建堆的时间复杂度是O(n),所以采取向下建堆会更优一些。
以上过程都是对小堆的建立,如果要建大堆,只需要将判断条件略作更改即可:
//建小堆
if (a[child] < a[parent])
if (child + 1 < size && a[child + 1] < a[child])
if (a[child] < a[parent])
//建大堆:
if (a[child] > a[parent])
if (child + 1 < size && a[child + 1] > a[child])
if (a[child] > a[parent])
堆的操作链接
最后,对于堆的各种操作需求,可以参考阿顺的这篇堆(C语言实现)











![Yocto系列讲解[技巧篇]90 - toolchain交叉编译器SDK中安装的软件](https://img-blog.csdnimg.cn/f64e1f114d7045eaa57a680daec4395b.png)