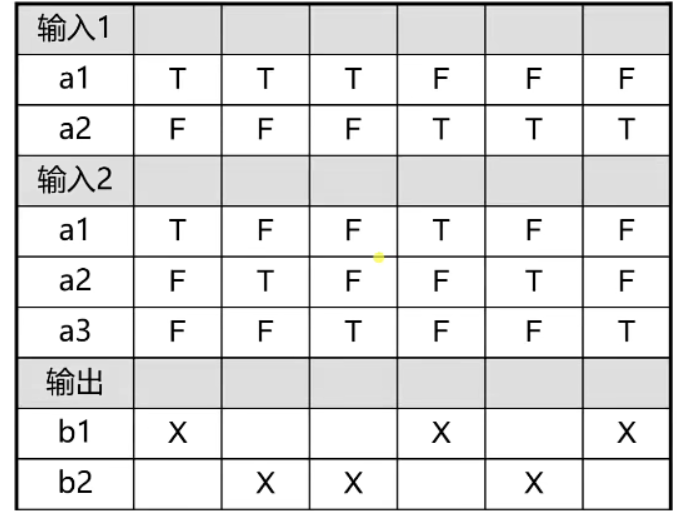
等价类划分法

测试一个两位数的加法计算器

测试需求： 测试两个参数的值相加后的结果是否正确

• 其中：输入的数值在-99到99之间，大于99或小于-99的输入应被拒绝，并显示错误信息

  • 

• 根据测试需求，我们开始测试

• 分别给第一个参数和第二个参数输入表中的值，得到的测试结果如表所示：

很明显，如果我们对第一个参数的值分别取从-99到99的199个数，第二个参数也是如此。我们不可能对两位数相加的所有情况进行穷举测试。

如果不能进行穷举测试我们将面临以下问题

这个时候，

• 等价类划分的方法是把程序的输入域划分成若干个部分

• 然后每个部分中选取少数代表性数据当做测试用例

• 每一类的代表性测试数据在测试中的作用等价于这一类中的其他值

• 也就是说，如果某一类中的一个例子中发现了错误，这一等价类中的其他例子也能发现同样的错误

• 反之，如果某一类中的一个例子没有发现错误，则这一类中的其他例子也不会查出错误

等价类划分原则

• 如果输入条件规定了取值的范围或值的个数，则可以确定一个有效等价类和两个无效等价类（三个阶段）
• 如果一个输入条件说明了一个必须成立的情况，则可划分一个有效等价类和一个无效等价类(bool型的条件)
• 如果输入条件规定了输入数据的一组可能的值，而且程序是用不同的方式处理每一种值，则每一种值划分一个有效等价类，并划分一个无效等价类地铁在进站的时候，一个人直接放心，两个人进展，一个人进展，一个人等待。
• 如果我们确知，已划分的某等价类中的各元素在程序中的处理方式是不同的，则因据此等价类进一步划分成更小的等价类
• 在确立了等价类之后，建立等价类表，列出所有划分出的等价类

基于等价类划分的用例设计

• 明确测试对象，非测试对象保证正确
• 为每个等价类规定一个唯一的编号
• 设计一个新的测试用例，使其能够尽可能多的覆盖尚未覆盖的有效等价类。重复这一步，最后使得所有有效等价类均被测试用例所覆盖
• 设计一个新的测试用例，使其只覆盖一个无效等价类。重复这一步使所有无效等价类均被覆盖。

等价类划分实战

• 根据测试需求可以划分成三个等价类
  • 一个有效数据的等价类，两个无效数据等价类
  • 有效数据等价类就是：由那些对程序的规格说明有意义的，合理的输入数据所构成的集合
  • 无效数据等价类就是：那些对程序的规格说明不合理的或者无意义的输入数据所构成的集合

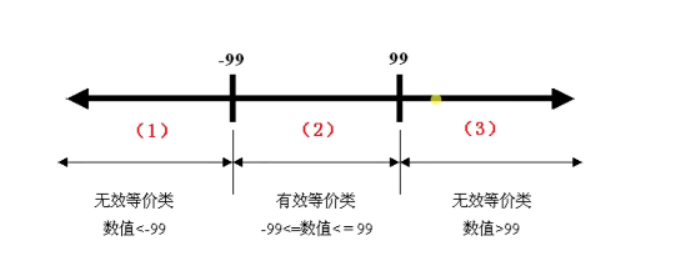
• 建立等价类表

  • 在实际工作中，我们通常在确立了等价类以后，把程序所有的等价类建立等价类表，以便在编写测试用例的时候有所依据

• 确定测试用例

  

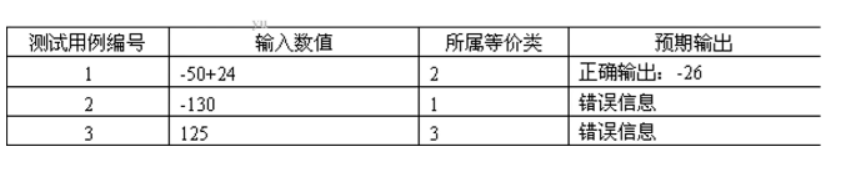
• 细化等价类划分

  • 在测试“-99<=数值<=99”的这个等价类区间的时候
  • 我们会发现如10+40，-20+30和-30+(-30)这类的正数相加，正数负数相加，负数相加也是不同的等价区间
  • 因此我们可以使用更多的等价类划分

• 根据以上等价类划分的结果，得出下表的等价类表

• 完善测试用例

  • 根据上面划分的四个等价类，我们至少需要有5个测试用例

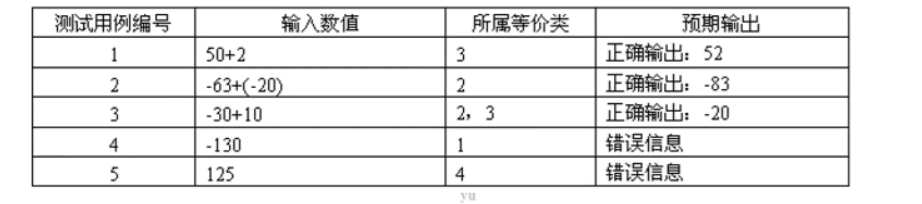
等价类划分的特点

主要就是画圈。要基于这个原则，把所有可能的输入作为一连串的输入。

我们会发现无效等价类还有可细分的空间，因为我们默认无效等价类只有数字，如果填上ABC，如果填上中文汉字呢？

所以，无效等价类还要进一步拆分，如果是数字、特殊字符、中文，你又要做如何判断？所以更细节的拆分如下，这需要大家课下考虑

• 测试相同的内容
• 如果等价类的一个测试能够捕获一个缺陷，那么选择该等价类的其他测试也能捕获该缺陷
• 如果等价类中的一个测试不能捕获缺陷，那么选择该等价类中的其他测试也不会捕获缺陷
• 如果正确的划分等价类，可以大大降低测试用例的数量，测试会准确有效
• 如果错误的将两个不同的等价类当做一个等价类，那就回遗漏一种测试情况
• 相反的，把同一个等价类看作了两个不同的等价类，那么测试就会是冗余的

等价类划分要注意的问题

• 不但要考虑有效等价类，也要考虑无效等价类
• 仔细划分，审查划分
• 过于粗略可能会漏掉软件缺陷

等价类用例设计联系

测试需求：余额宝体现到银行卡增加新规则：快速到账（2小时）日限额1w元

超过1万元只能选择普通到账

分析过程

• 设计用例

• 

• 细致分析需求，日限额1w，所以要区分两个场景

• 

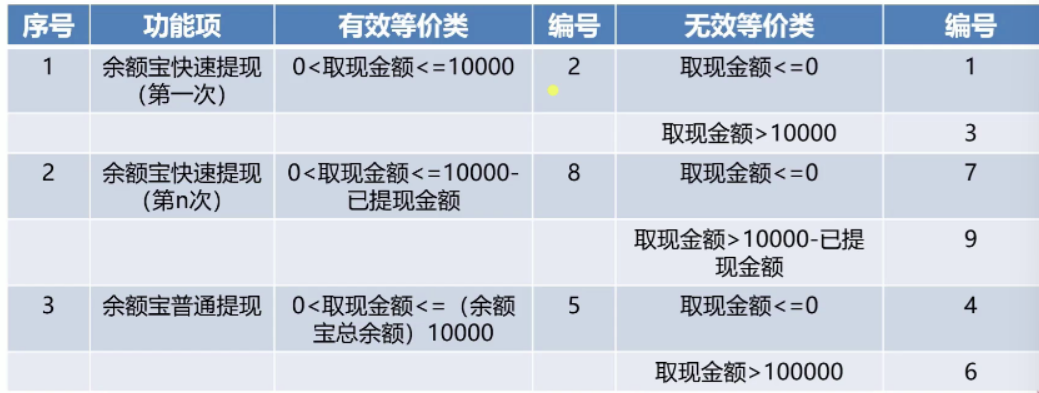
经典等价类划分面试题

• 问题：根据下面给出的规格说明，利用等价类划分的方法，给出足够的测试用例
• 一个程序读入三个整数，把这三个数值看做一个三角形的三条边的长度值
• 这个程序要打印出信息，说明这个三角形是不等边的，是等要的还等边的两边之和大于第三边（这是隐含条件的）

解答

1. 如果出结果只有两种：能构成三角形和不能构成三角形，那么有效等价类就只有abc均大于0，a+b>C,a+c>b,b+c>a

   然后题中规定输出三种结果“不等边、等腰、等边”所以等价类划分应该以此为依据

2. 有效等价类和无效类是否需要对应？每个功能点是否必须同时具有有效类和无效类？

   1. 有效类和无效类之间并没有一一对应的关系，可以分开划分。一个功能点会产生多个用例，用例通过不同是设计方法来实现，所以功能点跟等价类并没有对应关系

3. 是否需要考虑输入数字的先后关系？

   1. 如果是三个不同入参，在设计用例时，对a,b,c分别进行区分

		有效等价类	无效等价类
输入条件	读入三个整数a,b,c	1. 整数 2. 三个数 3. 非0 数 4. 正数	13. 一边为非整数 14. 两边为非整数 15. 三边为非整数 16. 数字个数小于3 17. 数字个数大于3 18. 一边为0 19. 两边为0 20. 三边为0 21. 一边小于0 22. 两边小于0 23. 三边小于0 24 一边大于100 25. 两边大于100 26. 三边大于100
输出条件	构成不等边三角形	5. a+b>c 6. a+c>b 7. b+c>a	27. a+b<=c 28. b+c<=a 29. c+a<=b
	构成等腰三角形	8. a=b且满足5 9. b=c且满足7 10. a=c且满足6
	构成等边三角形	11 a=b=c
	不构成三角形	12. 不满足5,6,7中的一个

等价类划分测试用例

等价类划分测试用例
测试用例编号	等价类条件	测试用例	预期结果
a	b	c	d
1	1,2,3,4,5,6,7	2	3	4		普通三角形
2	1,2,3,4,5,6,7,8	2	2	3		等腰三角形
3	1,2,3,4,5,6,7,9	2	3	2		等腰三角形
4	1,2,3,4,5,6,7,10	3	2	2		等腰三角形
5	1,2,3,4,5,6,7,11	2	2	2		等边三角形
6	1,2,3,4,12	1	2	3		不构成三角形
7	1,2,3,4,5,6,7,13	2.1	3	4		不构成三角形
8	1,2,3,4,5,6,7,14	2.1	2.1	3		不构成三角形
9	1,2,3,4,5,6,7,15	2.1	2.1	2.1		不构成三角形
10	1,3,4,16	2	3	null		不构成三角形
11	1,2,18	0	2	3		抛出异常
12	1,2,19	0	0	2		抛出异常
13	1,2,20	0	0	0		抛出异常
14	1,2,3,21	-1	2	2		抛出异常
15	1,2,3,22	-1	-2	2		抛出异常
16	1,2,3,23	-2	-2	-2		抛出异常
17	1,2,3,4,24	111	99	99		抛出异常
18	1,2,17	2	3	4	3	不构成三角形