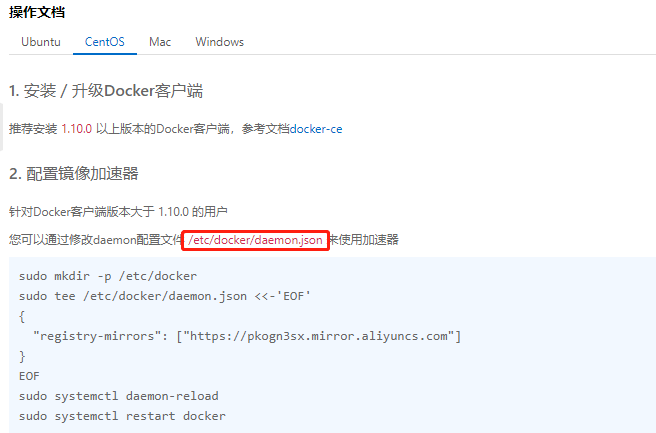
文章目录
- 一、二叉树的概念及结构
- 1.概念
- 2.现实中的二叉树
- 3. 特殊的二叉树:
- 3.二叉树的性质
- 二、二叉树练习题
- 总结
一、二叉树的概念及结构
1.概念
一棵二叉树是结点的一个有限集合,该集合:
- 或者为空
- 由一个根节点加上两棵别称为左子树和右子树的二叉树组成
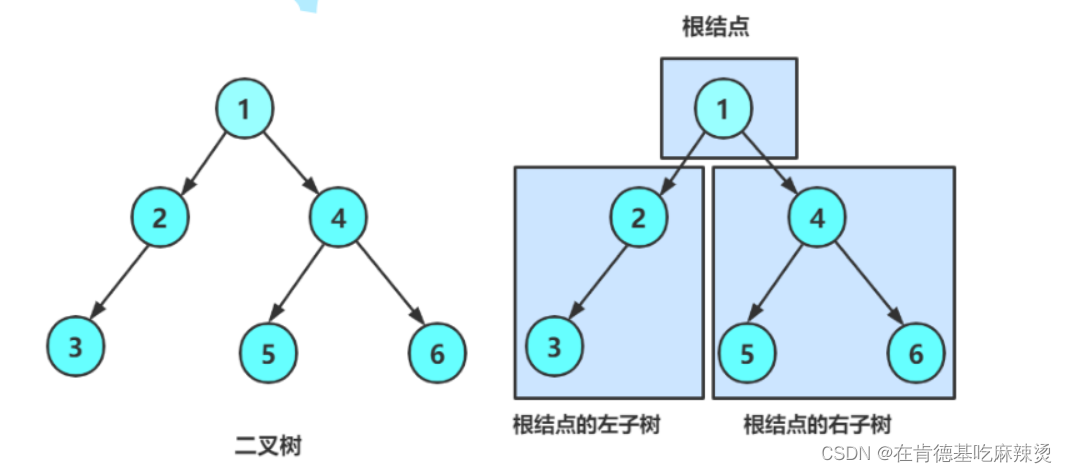
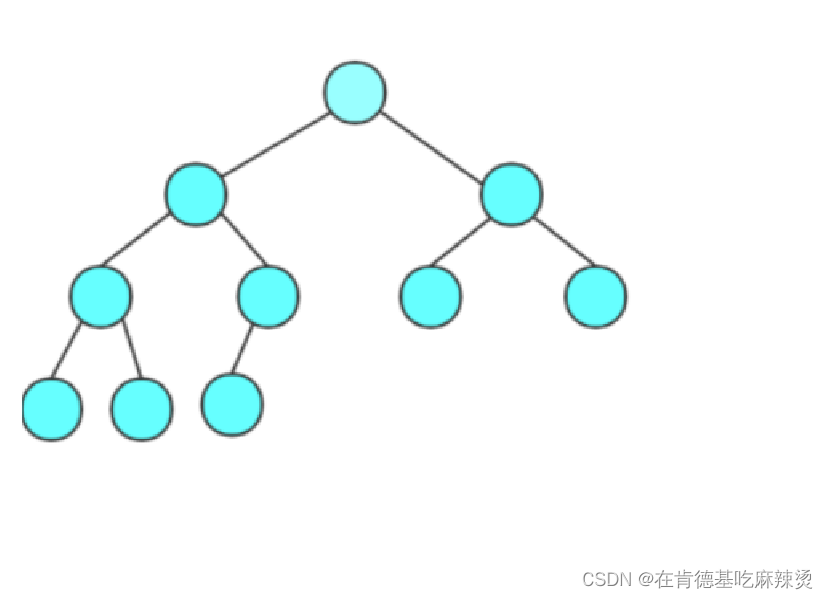
如上图就是二叉树,可以看出:
1.二叉树每个节点的度<=2
2. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
注意:对于任意的二叉树都是由以下几种情况复合而成的:
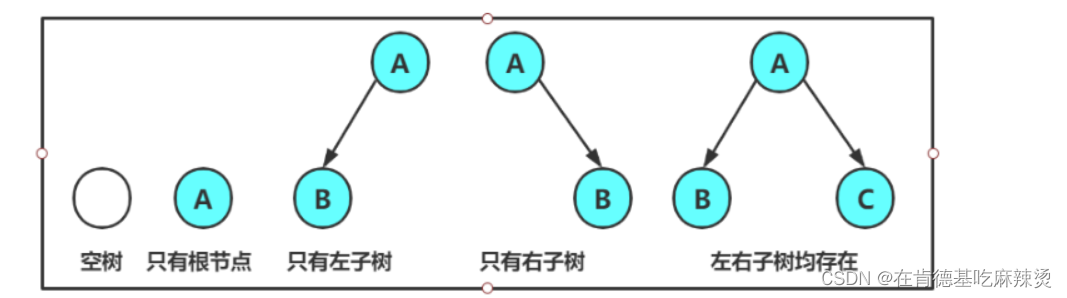
2.现实中的二叉树

3. 特殊的二叉树:
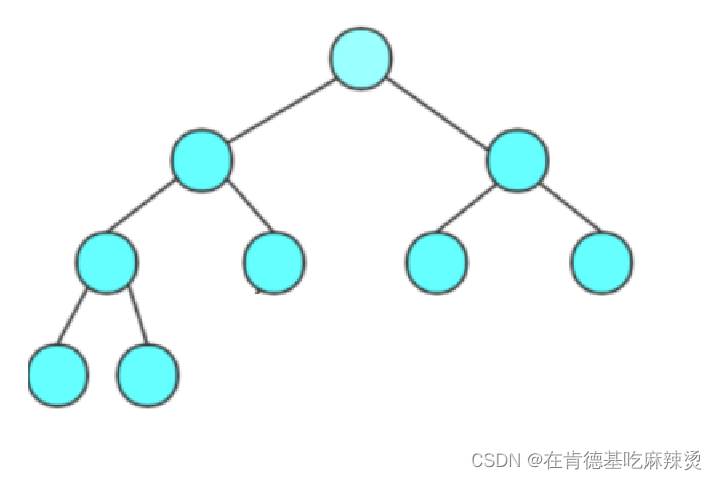
1)满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是2^K-1 ,则它就是满二叉树。
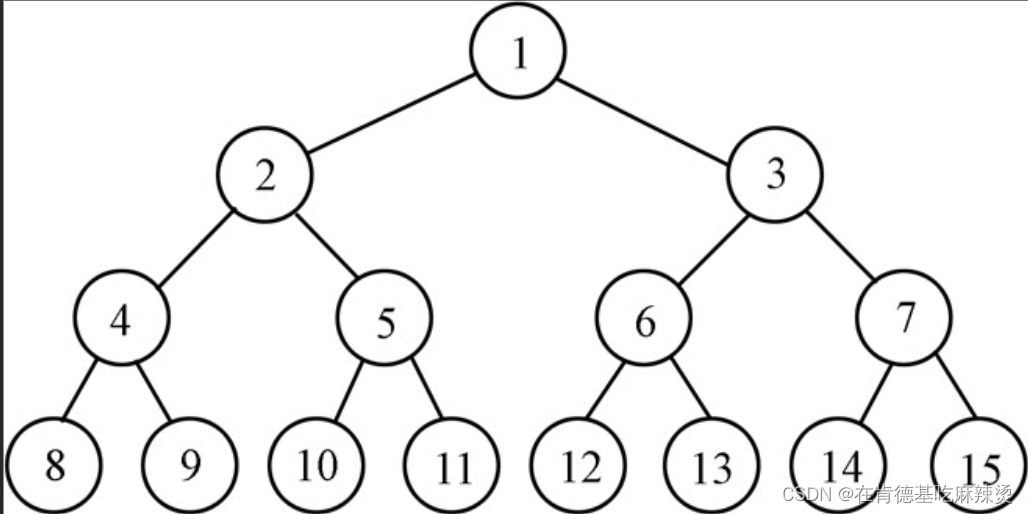
如上图:这是一棵满二叉树:
推导:
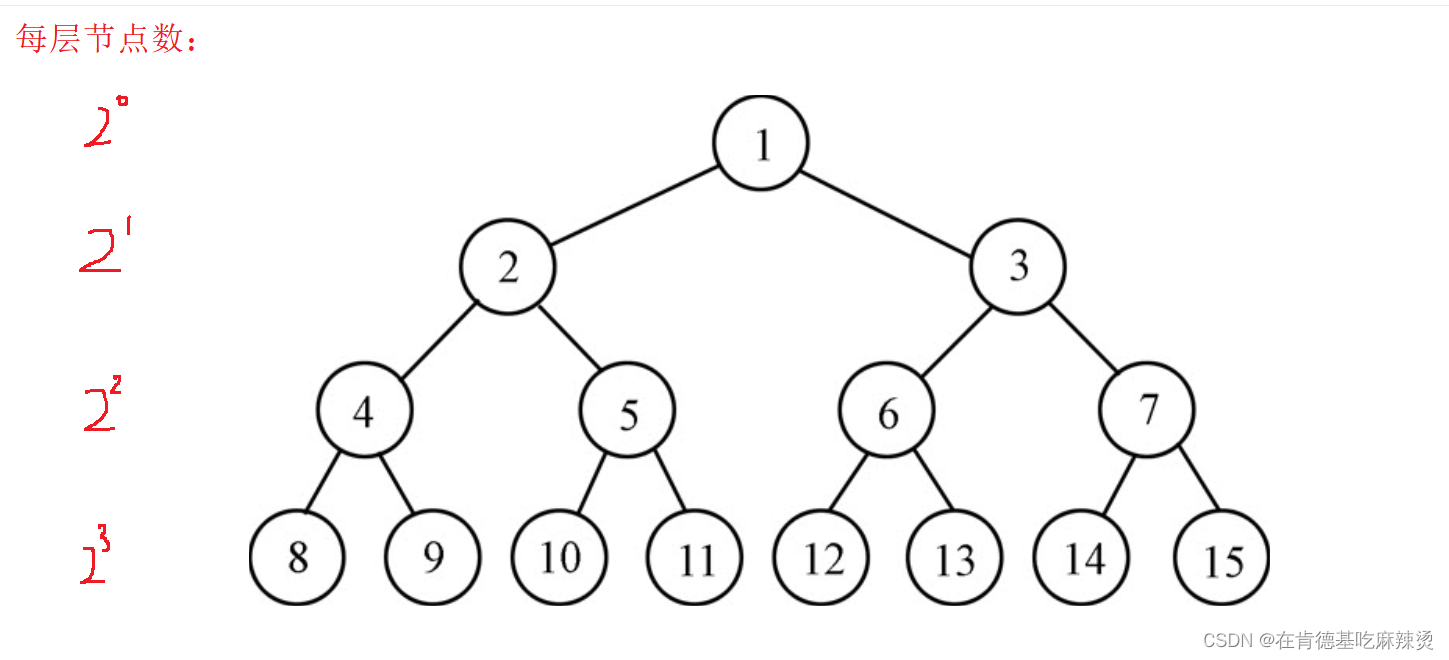
该二叉树的高度是h = 4.
则该二叉树的节点总数Sn = 2^0 + 2^1 + 2^2 + …+2^h-1
由等比数列求前n项和公式:

带入数据:
有 Sn = 2^h -1 (Sn为二叉树节点总数,h为树的高度)
所以这就是一棵标准的满二叉树。
如果我们知道一棵满二叉树的总节点个数,也可以推导出改满二叉树的节点的高度
推导如下:

h = log2(Sn+1)
2)完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。
通俗地讲:
1)前面每层节点的度都是2
2)最后一层节点必须连续
要注意的是满二叉树是一种特殊的完全二叉树。
比如说下面这个:
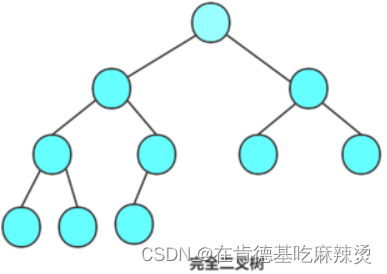
解释如下:
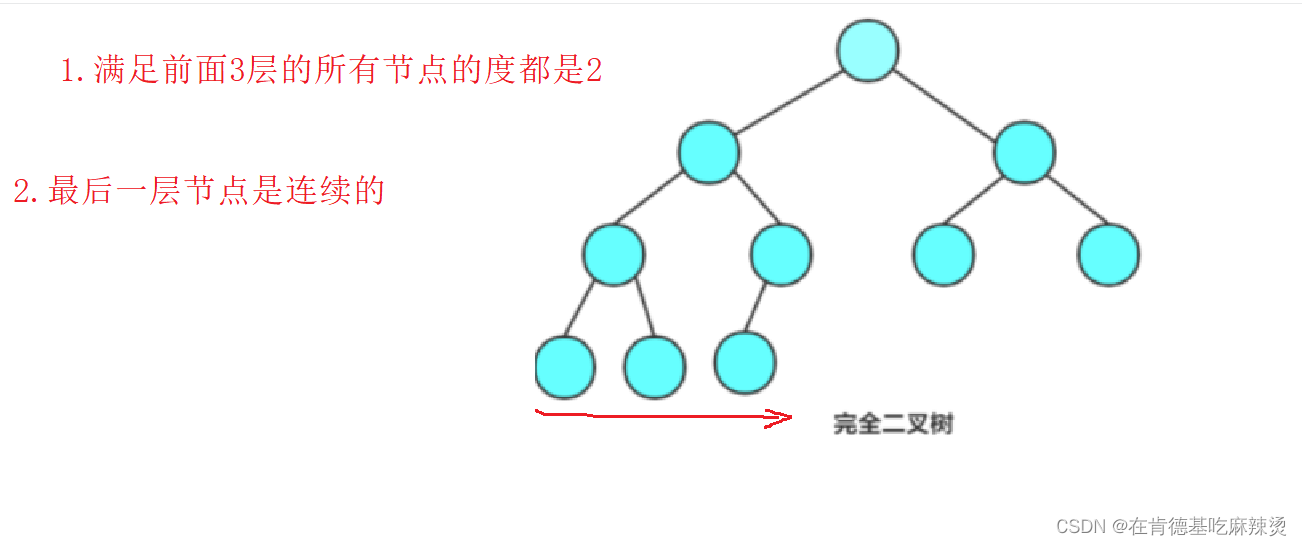
如果是这几种情况,就不是完全二叉树:
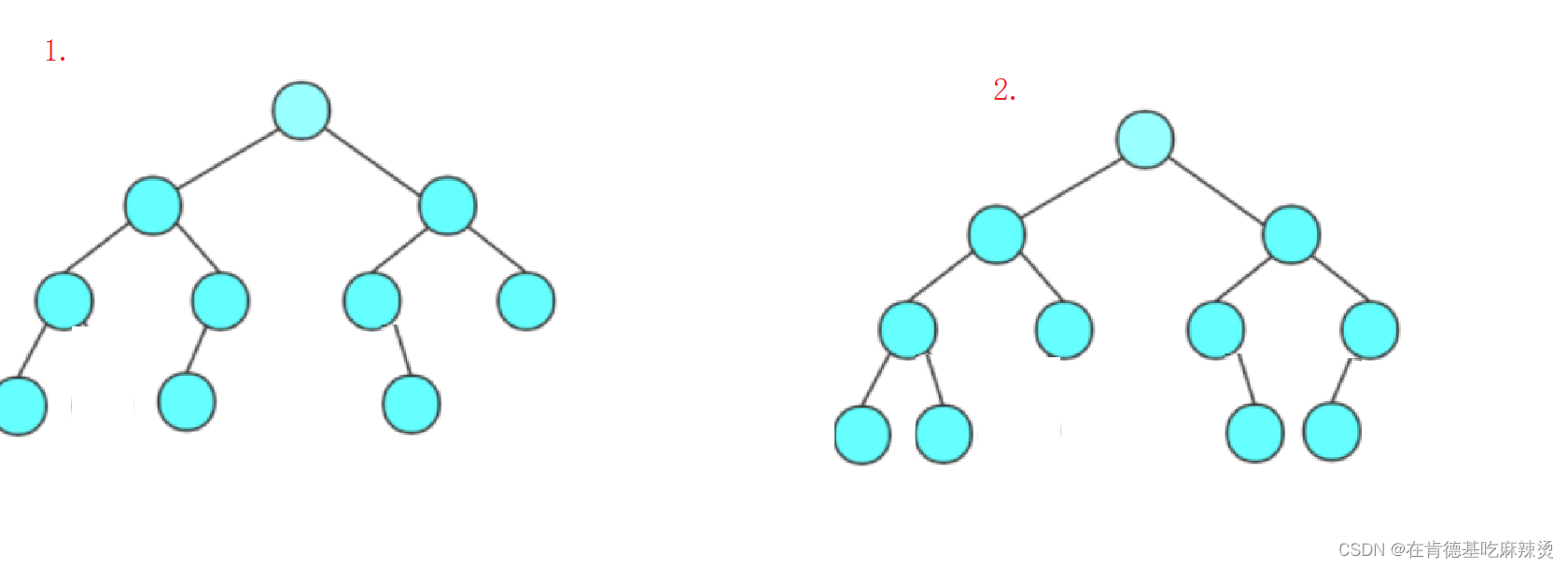
因为它们不符合第二点要求:最后一层是连续的。
由满二叉树和二叉树的定义可知,满二叉数是特殊的完全二叉树。
类似地:当我们知道完全二叉树的节点数,可以推导完全二叉树的高度:
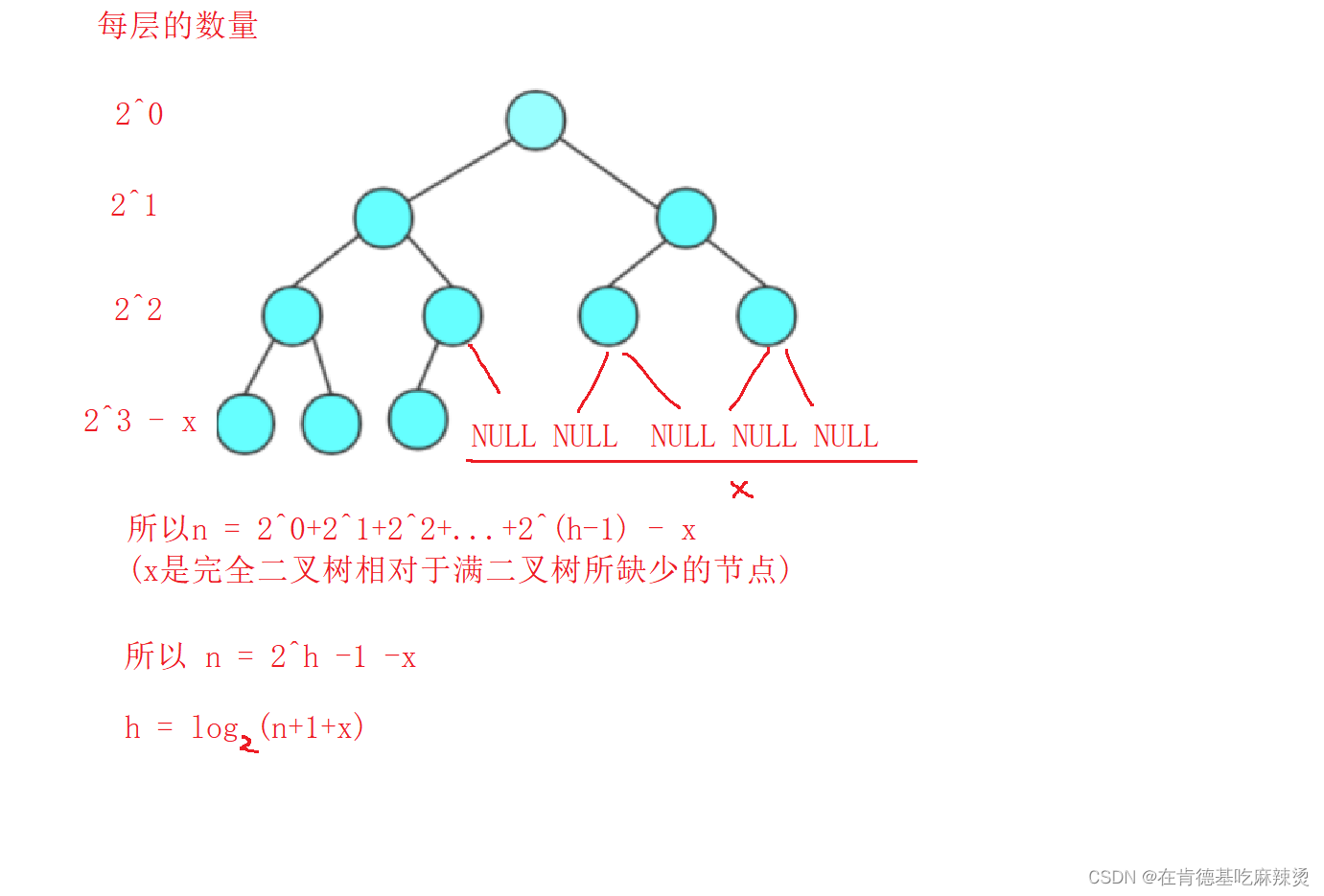
3.二叉树的性质
1. 若规定根节点的层数为1,则一棵非空二叉树的第n层上最多有2^(n-1) 个结点.
2. 若规定根节点的层数为1,则深度为h的二叉树的最大结点数是2^h - 1 .
3. 若规定根节点的层数为1,具有n个结点的满二叉树的深度,h= log2(n+1). (ps: 是log以2为底,n+1为对数)
4. 对任何一棵二叉树, 如果度为0其叶结点个数为n0, 度为2的分支结点个数为n2 ,则有 n0= n2+1
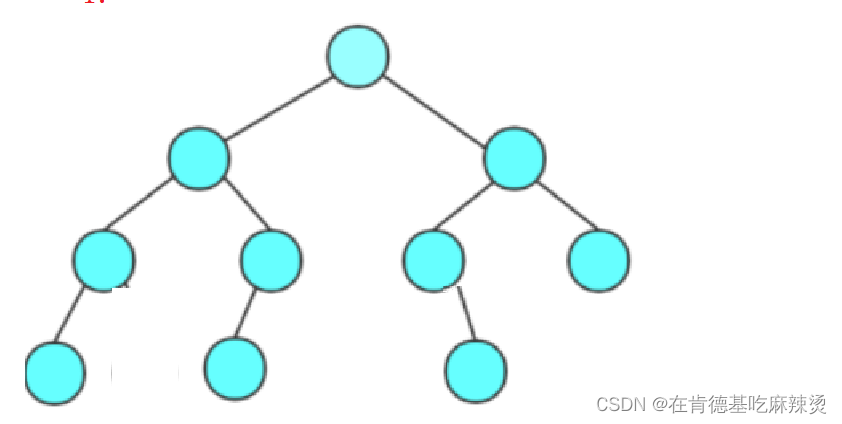
第四点解析:
以下图为例,度为0的节点的个数有4个,度为2的节点的个数有3个,则n0 = n2 + 1
5. 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对
于序号为i的结点有:
1)若i>0,i位置节点的双亲序号:(i-1)/2;i=0,i为根节点编号,无双亲节点
2)若2i+1<n,左孩子序号:2i+1,2i+1>=n否则无左孩子
3) 若2i+2<n,右孩子序号:2i+2,2i+2>=n否则无右孩子
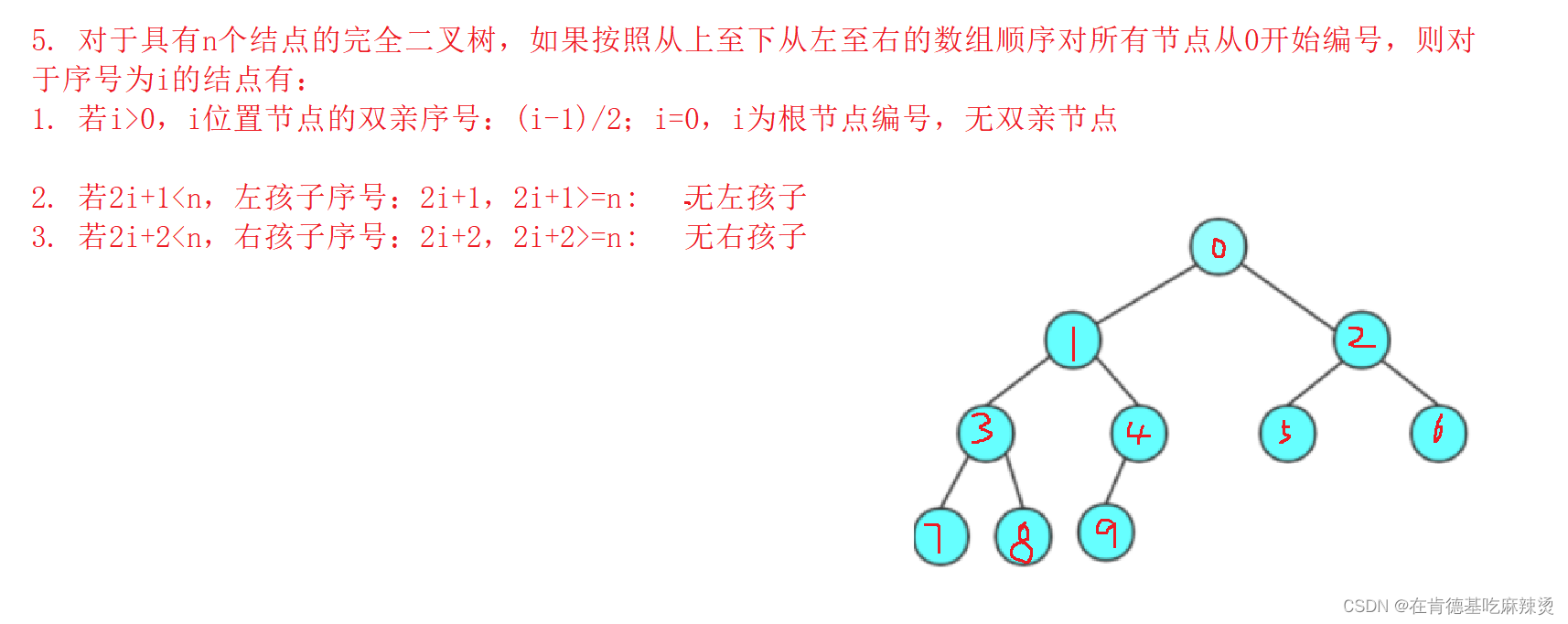
以该例子为例套进去即可。
前面三点是上面推导过的,第四点和第五点是重点要记忆的
二、二叉树练习题
1. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,
则该二叉树中的叶子结点数为( )
A 不存在这样的二叉树
B 200
C 198
D 199
解析:
运用上面所讲的性质四即可秒杀。
4. 对任何一棵二叉树, 如果度为0其叶结点个数为n0, 度为2的分支结点个数为n2 ,则有 n0= n2+1度为2的节点有199个,即n2 = 199,那么度为n0的节点 = n2+1 = 200
2.在具有 2n 个结点的完全二叉树中,叶子结点个数为( )
A n
B n+1
C n-1
D n/2
解析:
假设这棵完全二叉树的度为0,1,2的节点个数分别为:
x0 ,x1,x2
有: x0+x1+x2 = 2n
又根据性质四,x0 = x2 + 1,所以化简一下得:
x2+1+x1+x2 = 2n
对于一棵完全二叉树来说,度为1的节点的个数要么为0,要么为1
以上面这棵完全二叉树为例,度为1的节点只有1个
以上面这棵完全二叉树的节点为例:度为1的节点有0个。
所以对于任何一颗完全二叉树来说,度为1的节点只有1个或0个。
则x1 = 1或x1 = 0
当x1 = 1时,
x2+1+x1+x2 = 2n -->2*x2 + 2 = 2n,
所以x2 = n而当x1 = 0时,2*x2+1 = 2n,x2 = (2n-1)/2,节点个数不可能为小数,所以不成立
所以该完全二叉树的度为1的节点个数为n
3.一棵完全二叉树的节点数位为531个,那么这棵树的高度为( )
A 11
B 10
C 8
D 12
解析:
以这棵二叉树为例:
对于一棵完全二叉树,节点个数与高度的关系有:
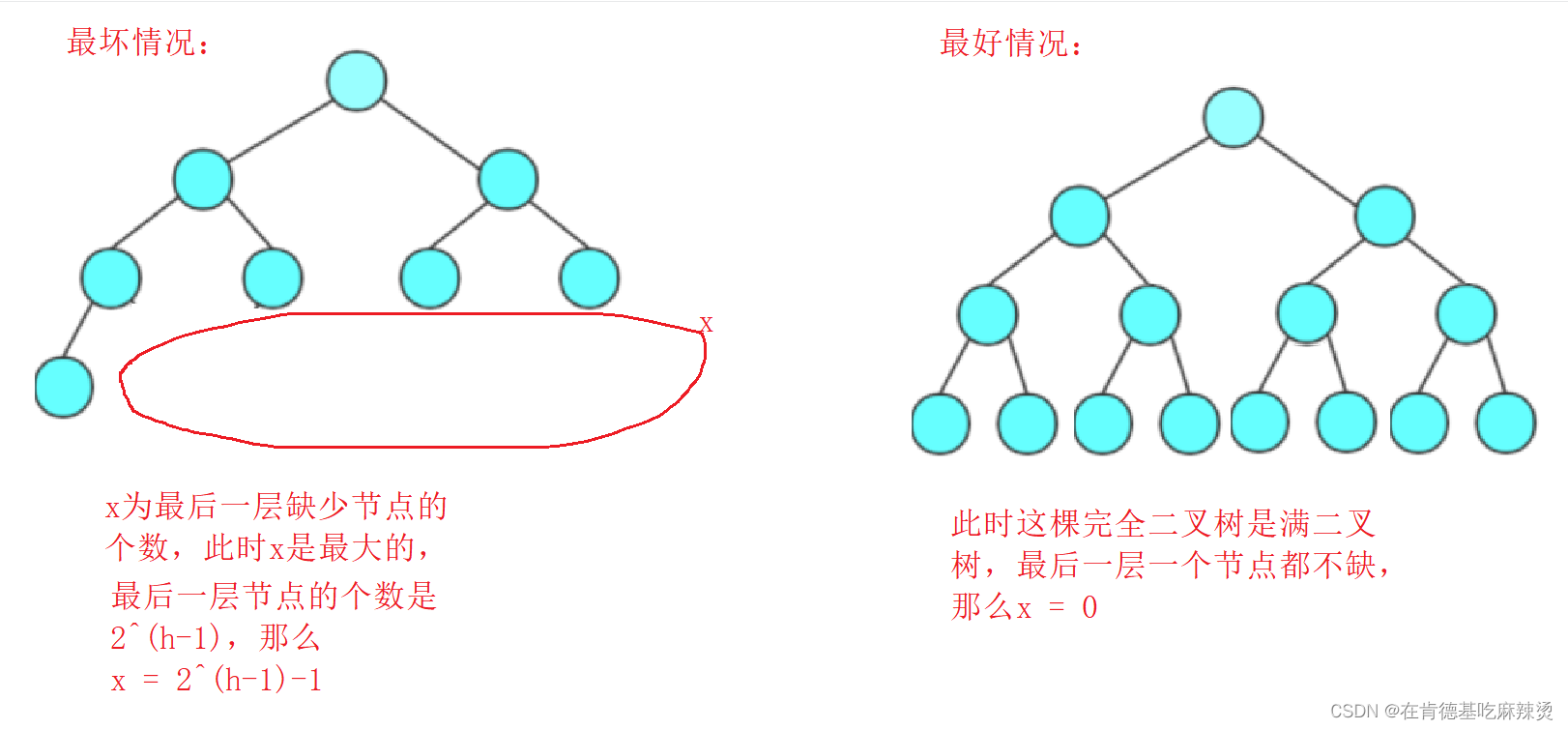
n = 2^h-1-x(x为完全二叉树最后一层中缺少的节点的个数)
缺少的节点是相对于满二叉树来说的。
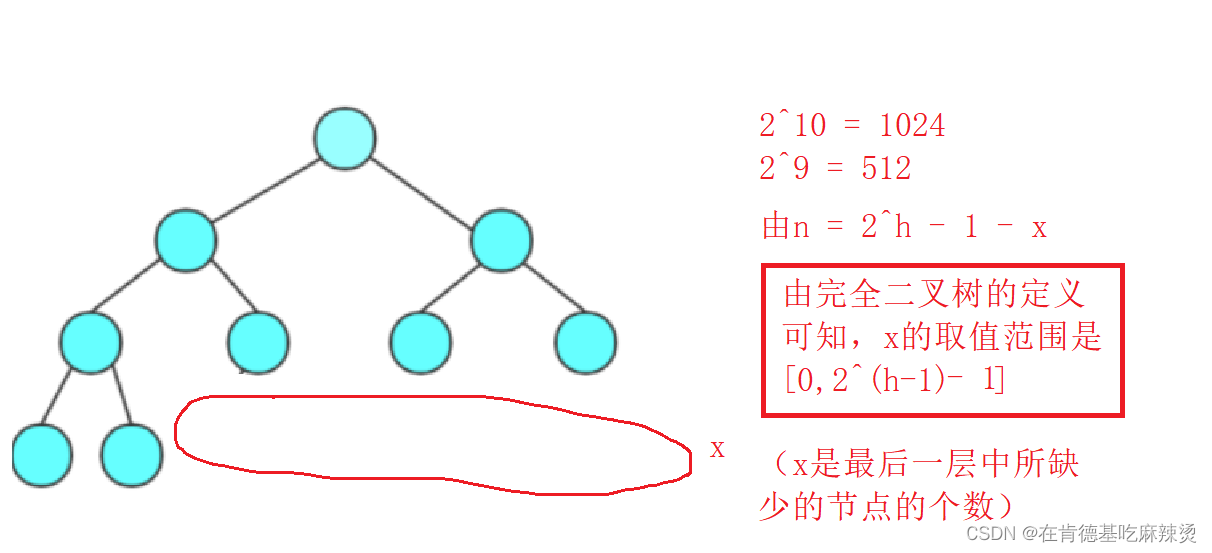
x的最好情况和最坏情况如下:
当h = 10时,节点个数为 2^10 - 1 - x ,
此时x的取值范围是[0,2^9-1-1],即[0,510]
代入原数据 531 = 2^10 -1 -x,x = 492,在取值范围内。当n = 11时,节点个数为2^11 -1 -x,
此时x的取值范围是[0,2^10-1-1],即[0,1022]
代入原数据 531 = 2^11 -1 -x,x = 1516,不在取值范围内,不成立。
而对于当h = 12时,更不可能了。
对与h = 8,2^8 = 256,也不可能
所以h = 10,选B
4.一个具有767个节点的完全二叉树,其叶子节点个数为()
A 383
B 384
C 385
D 386
解析:
这道题的解法与第2题解法相同
直接画图分析:
总结
熟知二叉树的相关知识概念和性质,非常有助于进一步二叉树广度优先搜索和深度优先搜索的学习。