---

1.单链表

1.1单链表的表示

单链表中节点类型的描述如下：

typedef struct LNode{
	ElemType data;	//数据域
	struct LNode *next;	//指针域
}LNode,*LinkList;

1.1.1构建 带头结点的单链表

typedef struct LNode{	//定义单链表结点类型
	ElemType data;		//每个结点存放一个数据元素
	struct LNode *next;	//指针指向下一个节点
} LNode,*LinkList;

//初始化一个单链表（带头结点）
bool InitList(LinkList &L){
	L=(LNode*)malloc(sizeof(LNode));	//分配一个头结点
	if(L==NULL)			//内存不足，分配失败
		return false;
	L->next=NULL;	//节点之后暂时还没有节点
	return true;	
}

void test(){
	LinkList L;		//声明一个指向单链表的指针
	//初始化一个空表
	InitList(L);
	//后续代码...
}

//判断单链表是否为空（带头结点）
bool Empty(LinkList L){
	if(L->next==NULL)
		return true;
	else
		return false;
}

---

1.2基本操作

受某些限制，没法把动画效果做出来，看看图理解一下吧~

强调这是一个单链表使用LinkList
强调这是一个结点使用LNode*

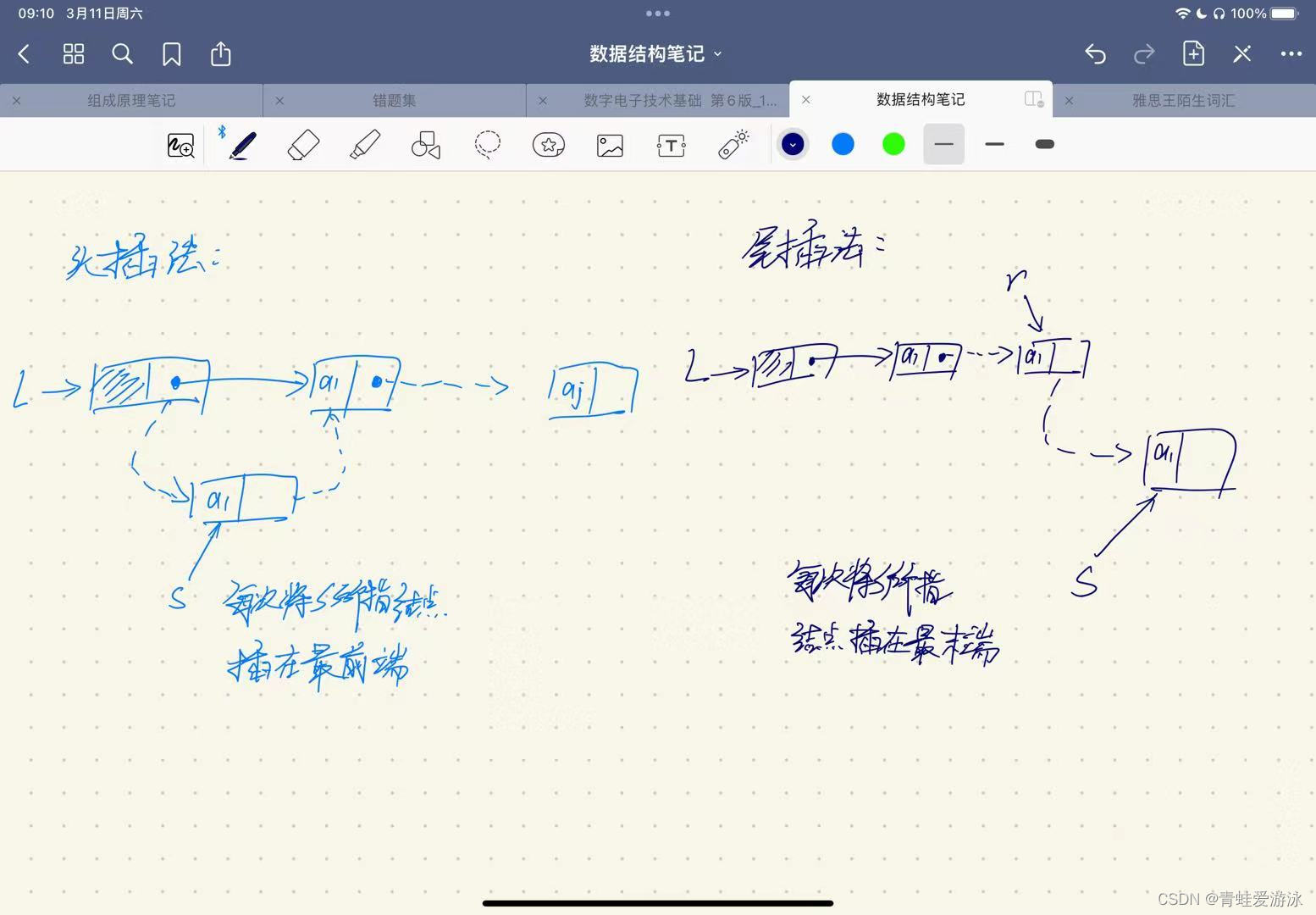
1.2.1 头插法

LinkList List_HeadInsert(LinkList &L){	//逆向建立单链表
	LNode *a;
	int x;
	L=(LinkList)malloc(sizeof(LNode));	//创建头结点
	L->next=NULL;	//初始为空链表
	scanf("%d",&x);	//输入节点的值
	while(x!=9999){	//输入9999表示结束
		s=(LNode*)malloc(sizeof(LNode));	//创建新结点
		s->data=x;
		s->next=L->next;
		L->next=s;	//将新结点插入表中
		scanf("%d",&x);
	}
	return L;
}

采用头插法建立单链表时，读入数据的顺序与生成的链表中的元素的顺序是相反的

时间复杂度为O(n)

1.2.2 尾插法

将新结点插入到当前链表的表尾，为此必须增加一个尾指针r，使其始终指向当前链表的尾结点

LinkList List_TailInsert(LinkList &L){	//正向建立单链表
	int x;	//设元素为整形
	L=(LinkList)malloc(sizeof(LNode));
	LNode *s,*r=L;	//r为表尾指针
	scanf("%d",&x);	//输入结点的值
	while(x!=9999){
		s=(LNode *)malloc (sizeof (LNode));
		s->data=x;	//新的数据为x
		r->next=s;	//r的下个结点指向s
		r=s;		//r指向s
		scanf("%d",&x);
	}
	r->nxt=NULL;	//尾结点指针置空
	return L;
}

时间复杂度为O(n)

1.2.3 按序号查找结点

LNode *GetElem(LinkList L,int i){
	if (i<1)
		return NULL;
	int j=1;	//计数，初始为1
	LNode *p=L->next;	//第一个结点指针赋值给p
	while(p!=NULL&&j<i){	//从第一个结点开始找，查找第i个结点
		p=p->next;
		j++;
	}
	return p;	//返回第i个结点的指针，若i大于表长，则返回NULL
}

时间复杂度为O(n)

1.2.4 按值查找表结点

LNode *LocateElem(LinkList L,ElemType e){
	LNode *p=L->next;
	while(p!=NULL&&p->data!=e)	//从第一个结点开始查找data域为e的结点
		p=p->next;
	return p;	//找到后返回该结点指针，否则返回NULL
}

1.2.5 插入结点操作

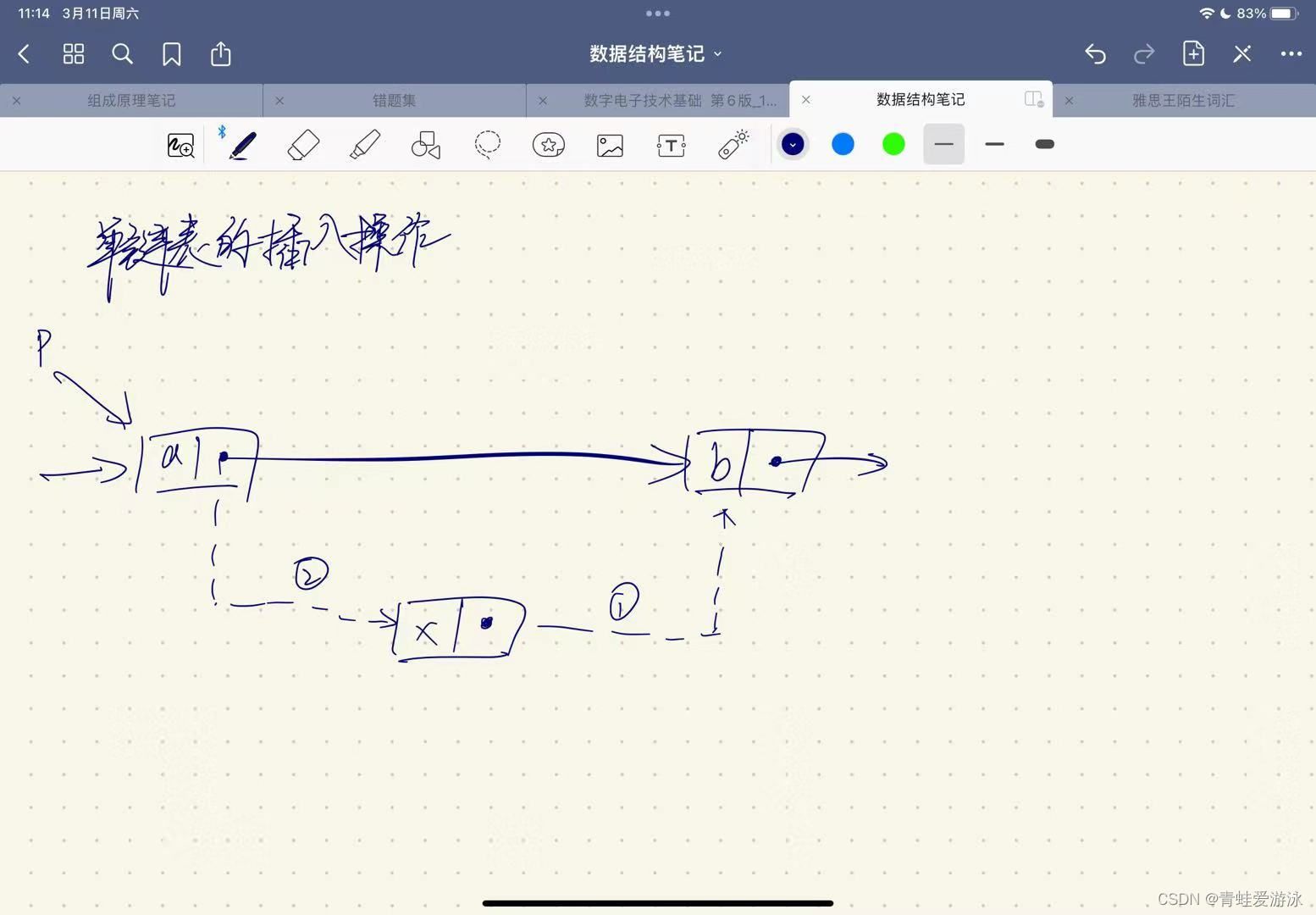
p=GetElem(L,i-1);	//查找插入位置的前驱结点
s->next=p->next;	//操作步骤1
p->next=s;			//操作步骤2

扩展：前插操作

设插入结点为s,将s插入到*p的后面，然后将p->data和s->data交换

//将*s结点插入到*p之前的主要代码片段
s->next=p->next;	//修改指针域,不能颠倒
p->next=s;
temp=p->data;		//交换数据域部分
p->data=s->data;
s->data=temp;

1.2.6 删除结点操作

假设p为找到的被删结点的前驱结点，仅需修改p的指针域，即将p的指针域next指向q的下一结点

p=GetElem(L,i-1);		//查找删除位置的前驱结点
q=p->next;				//令q指向被删除结点
p->next=q->next;		//将*q结点从链中断开
free(q);				//释放结点的存储空间

时间复杂度为O(n)

扩展：删除结点*p

删除结点可用删除*p的后继结点来实现，本质就是将其后继节点的值赋予其自身，然后删除后继结点，这样使得时间复杂度为O(1)

q=p->next;		//令q指向*p的后继结点
p->data=p->next->data;	//用后继结点的数据域覆盖
p->next=q->next;		//将*q结点从链中断开
free(q);		//释放后继结点的存储空间

1.2.7 求表长操作

统计数据结点的个数（不包含头结点），需要设置一个计数器

单链表的长度是不包括头结点的

---

2.双链表

2.1 双链表的表示

双链表结点中有两个指针prior和next，分别指向其前驱结点和后继结点

访问前驱结点的时间复杂度为O(n)
访问后继结点的时间复杂度为O(1)

双链表中结点类型的描述如下：

typedef struct DNode{	//定义双链表结点类型
	ElemType data;		//数据域
	struct DNode *prior,*next;	//前驱和后继指针
}DNode,*DLinkList;

2.2基本操作

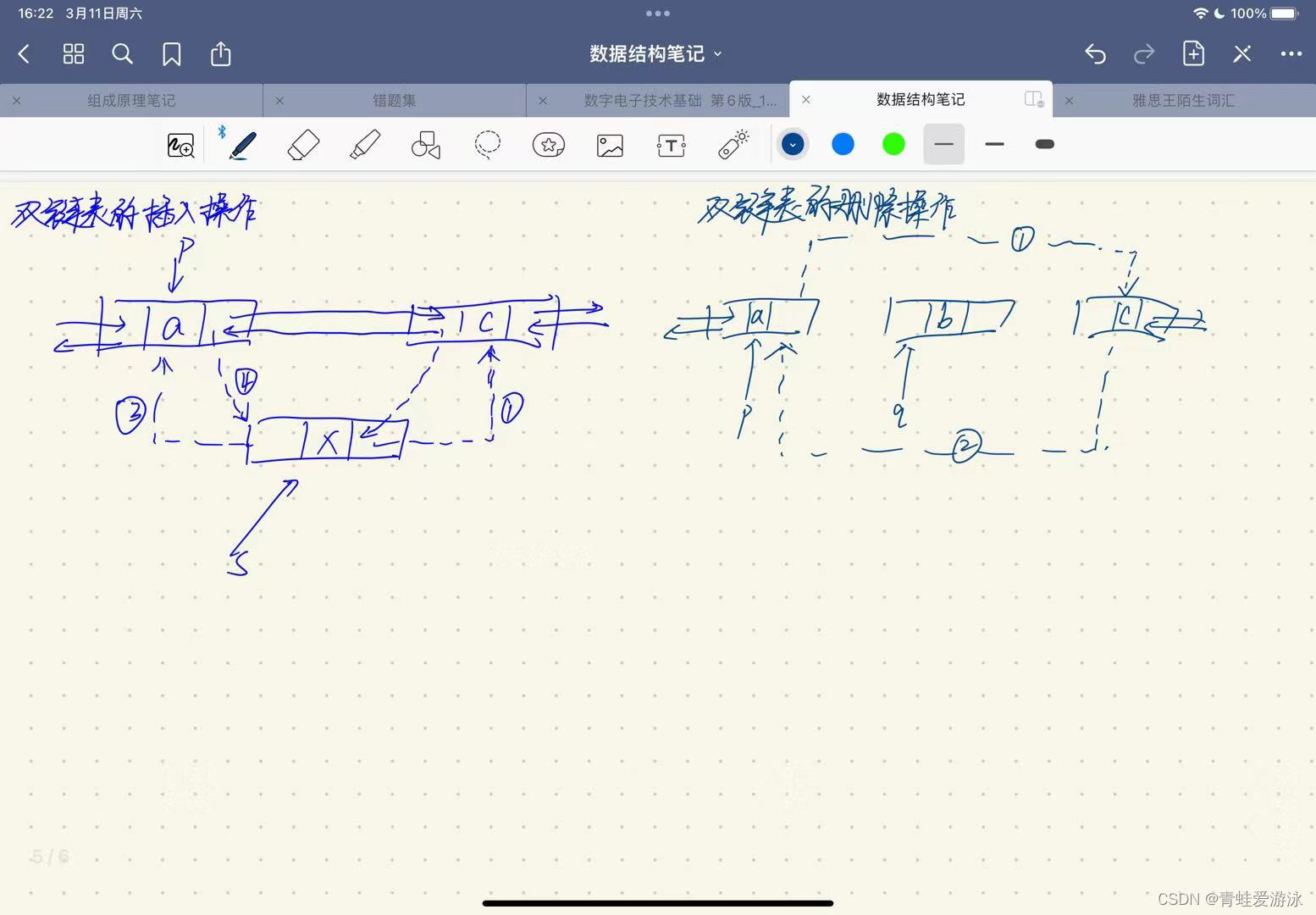
2.2.1 插入操作

s->next=p->next;	//将结点*s插入到结点*p之后
p->next->prior=s;
s->prior=p;
p->next=s;

2.2.2 删除操作

p->next=q->next;
q->next->prior=p;
free(q);

---

3.循环链表

3.1 循环单链表

表中最后一个结点的指针不是NULL，而改为指向头结点，从而整个链表形成一个环。

在循环单链表中，表尾结点*r的next域指向L，故表中没有指针域为NULL的结点，因此，循环单链表的判空条件不是头结点的指针是否为空，而是它是否等于头结点。

3.2 循环双链表

在循环双链表L中，某结点*p为尾结点时，p->next==L；当循环双链表为空表时，其头结点的prior域和next域都等于L。

---

4.静态链表

静态链表的指针是结点的相对地址（数组下标），又称游标。
和顺序表一样，静态链表也要预先分配一块连续的内存空间。

静态链表的结构类型：

# define MaxSize=50		//静态链表的最大程度
typedef struct{
	ElemType data;
	int next;			//下一个元素的数组下标
}SlinkList[MaxSize];