前言

密码，是指使用特定变换对数据等信息进行加密保护或安全认证的物项（承载算法、密钥、密文的介质）和技术，主要用于加密和安全认证（身份识别、完整性、抗抵赖性）。

密码按照保密等级，又分为核密、普密、商密三种，其中核密、普密用于涉及国家秘密领域，商密用于非涉及国家秘密领域。

接下来，我们重点讲一下这个商密。

什么是商用密码？

商密，全称商用密码，是国家密码局认定的国产密码算法，又称国密算法，为了保障商用密码的安全性，国家商用密码管理办公室制定了一系列密码标准，包括对称算法（SM1、SM4等），非对称算法（SM2、SM9）以及哈希算法（SM3）等等。

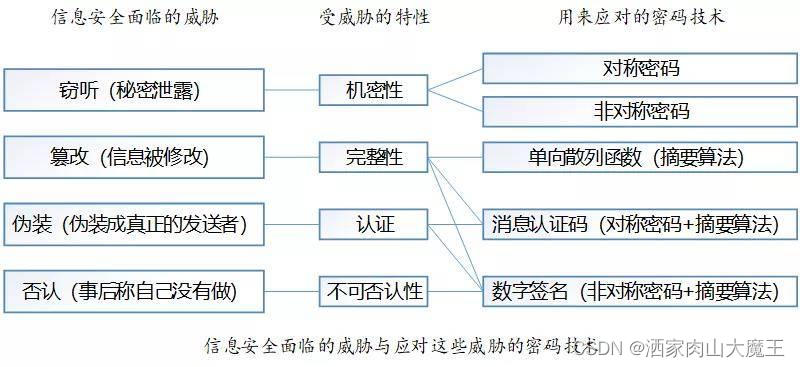
这些密码标准可以有效保护信息安全所面临的威胁，例如：

• 为防止信息被窃取、监听，避免秘密泄露，需要确保信息的机密性，可以使用对称加密与非对称加密对信息进行加密保护；

• 为防止信息被篡改，导致接收者收到错误的信息，可以使用数字签名、消息认证码、单向散列函数的技术，保证信息的完整性；

• 不少黑客会伪装成真正的发送者，给你发送虚假的信息，此时需要对发送者的身份进行认证，可使用消息认证码、数字签名的方式；

• 不可否认性也称不可抵赖性，可以保证在信息交互过程中所有参与者都不可能否认或抵赖曾经完成的操作和承诺甚至是“内鬼”行为，通过数字签名就可以保证信息的不可否认性。

什么是对称加密？

对称加密算法给定一个明文和一个密钥，加密产生密文，其长度和明文大致相同，解密时，使用的解密密钥与加密密钥相同，因此被称为对称加密算法。

国密算法的对称加密算法包括：SM1、SM4、SM7、ZUC祖冲之算法等。

由于SM1与SM7主要用于芯片、智能IC卡、智能密码钥匙、加密卡、加密机等安全产品，而SM4、ZUC祖冲之算法分别是运用于无线局域网产品与移动通信4G网络中的国际标准密码算法。这里我们重点介绍SM4和ZUC。

1. SM4算法定义

SM4密码算法是我国自主设计的分组对称密码算法，用于实现数据的加密/解密运算，以保证数据和信息的机密性。

1. 该算法的分组长度为128比特，密钥长度为128比特。（十六进制表示则为32位，明文和密钥等长）

2. 加密算法与密钥扩展算法都采用32轮非线性迭代结构。

3. 密钥扩展算法：将加密密钥变换为轮密钥的运算单元。

4. 数据解密和数据加密的算法结构相同，只是轮密钥的使用顺序相反，解密轮密钥是加密轮密钥的逆序。

---

2. SM4算法的优势

国密算法SM4有安全高效的特点，在设计与实现方面有以下优势：

• 对合运算：解密算法与加密算法相同，只是轮密钥的使用顺序相反，解密轮密钥是加密轮密钥的逆序。

• 子密钥生成算法与加密算法结构类似，在设计上做到资源重用。

• 加密算法与密钥扩展算法都采用32轮非线性迭代结构，将128位的明文、密钥通过32次循环的非线性迭代运算得到最终结果。

---

3. 加密算法流程

SM4加密的整体流程框架：

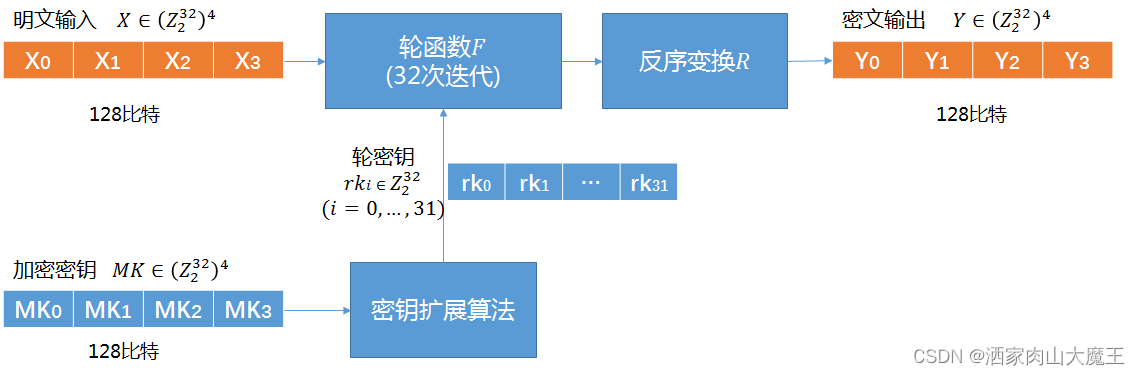
或者参考

北卡科技的博客中的流程图：

SM4算法结构：

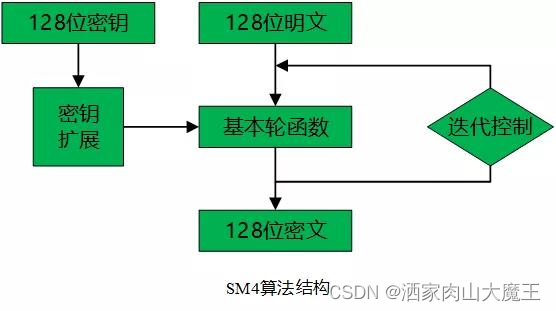
轮密钥生成：

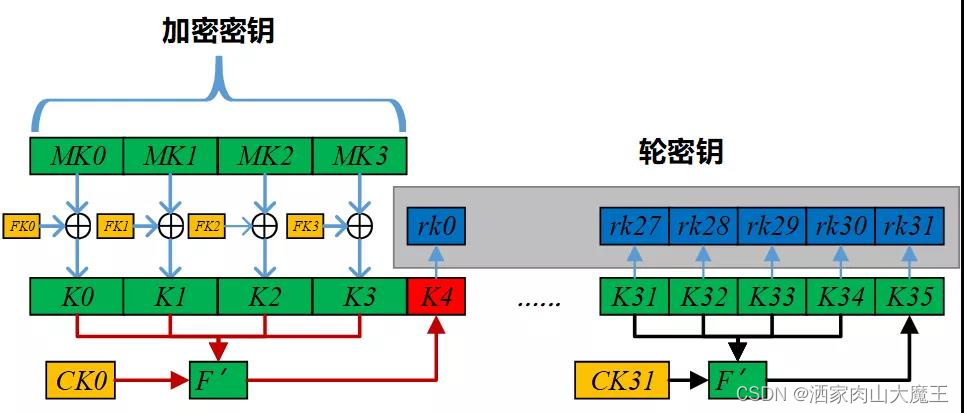
32次非线性迭代：

3.1. 密钥扩展算法

密钥扩展算法：将加密密钥变换为轮密钥的运算单元。

轮密钥 rkirki 生成方法：

rki=Ki+4=Ki⊕T′(Ki+1⊕Ki+2⊕Ki+3⊕CKi), i=0,1,⋯,31rki=Ki+4=Ki⊕T′(Ki+1⊕Ki+2⊕Ki+3⊕CKi), i=0,1,⋯,31。

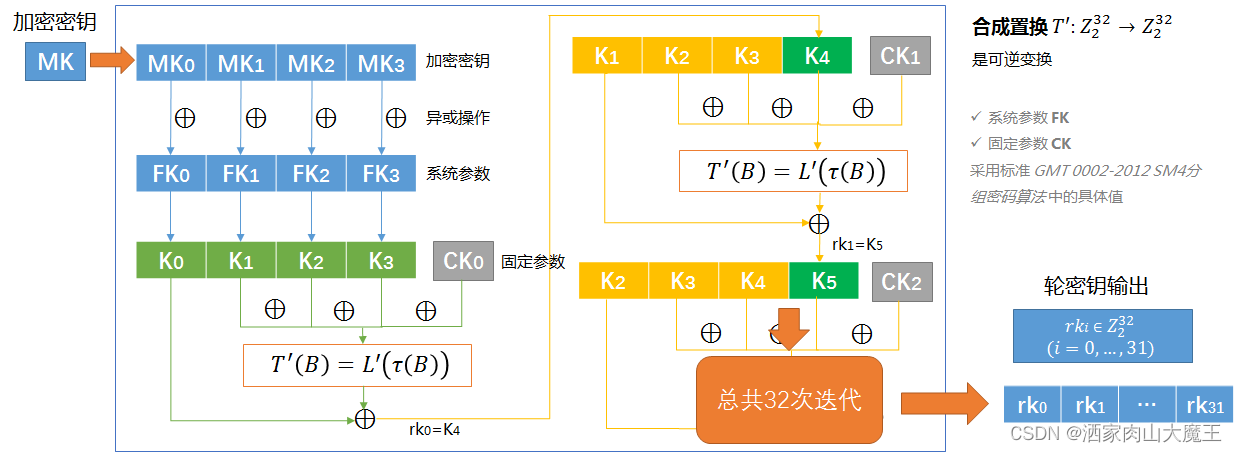
合成置换 T′:Z322→Z322T′:Z232→Z232 是一个可逆变换，由非线性变换 ττ 和线性变换 L′L′复合而成，即 T′(⋅)=L′(τ(⋅))T′(⋅)=L′(τ(⋅))。

线性变换 L′L′： L′(B)=B⊕(B<<<13)⊕(B<<<23)L′(B)=B⊕(B<<<13)⊕(B<<<23)，其中 <<<i<<<i 表示32位循环左移 ii 位。

非线性变换 ττ： τ(B)τ(B)，ττ 由4个并行的S盒构成。

S盒为固定的8比特输入8比特输出的置换，记为 Sbox(⋅)Sbox(⋅)。
轮密钥由加密密钥生成。
FK=(FK0,FK1,FK2,FK3)FK=(FK0,FK1,FK2,FK3) 为系统参数[^1]，CK=(CK0,CK1,⋯,CK31)CK=(CK0,CK1,⋯,CK31) 为固定参数[^2]，用于密钥扩展算法，其中 FKi (i=0,⋯,3)FKi (i=0,⋯,3) 、CKi (i=0,⋯,31)CKi (i=0,⋯,31) 为字。

[^1]：系统参数 FKFK 的取值为： FK0=(A3B1BAC6), FK1=(56AA3350), FK2=(677D9197), FK3=(B27022DC)FK0=(A3B1BAC6), FK1=(56AA3350), FK2=(677D9197), FK3=(B27022DC)。

[^2]：固定参数 CKCK 的取值方法为：设 cki,jcki,j 为 CKiCKi 的第 jj 字节(i=0,1,⋯,31; j=0,1,2,3i=0,1,⋯,31; j=0,1,2,3)，即 CKi=(cki,0,cki,1,cki,2,cki,3)CKi=(cki,0,cki,1,cki,2,cki,3)，则 cki,j=(4i+j)×7(mod256)cki,j=(4i+j)×7(mod256)。

固定参数 CKi(i=0,1,⋯,31)CKi(i=0,1,⋯,31) 具体值为：

非线性变换 ττ

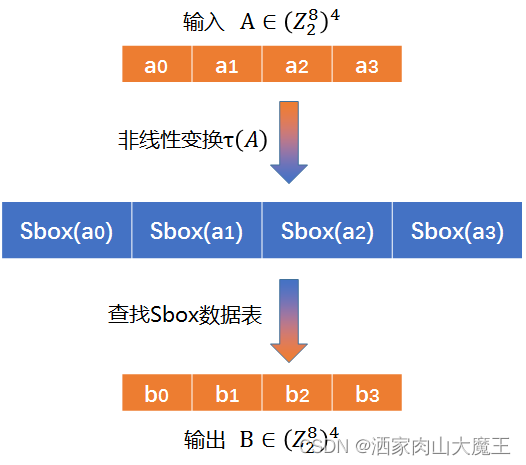
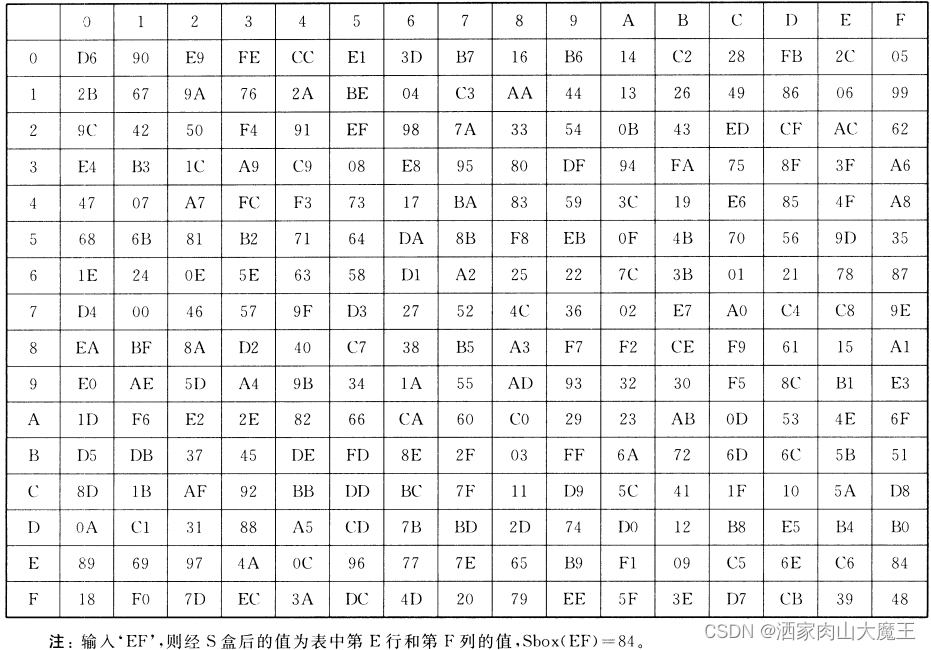
例如输入为 01 23 45 6701 23 45 67，则该 ττ 变换应为：90 F4 73 A290 F4 73 A2。(01→第0行第1列→9001→第0行第1列→90)

3.2. 轮函数 FF · 32次迭代

轮函数 FF 生成方法：

Xi+4=F(Xi,Xi+1,Xi+2,Xi+3,rki)=Xi⊕T(Xi+1⊕Xi+2⊕Xi+3⊕rki),i=0,1,⋯,31Xi+4=F(Xi,Xi+1,Xi+2,Xi+3,rki)=Xi⊕T(Xi+1⊕Xi+2⊕Xi+3⊕rki),i=0,1,⋯,31

合成置换 T:Z322→Z322T:Z232→Z232 是一个可逆变换，由非线性变换 ττ 和线性变换 LL复合而成，即 T(⋅)=L(τ(⋅))T(⋅)=L(τ(⋅))。

线性变换 LL： L(B)=B⊕(B<<<2)⊕(B<<<10)⊕(B<<<18)⊕(B<<<24)L(B)=B⊕(B<<<2)⊕(B<<<10)⊕(B<<<18)⊕(B<<<24)。

非线性变换 ττ： τ(B)τ(B)，ττ 由4个并行的S盒构成。

3.3. 反序变换 RR

---

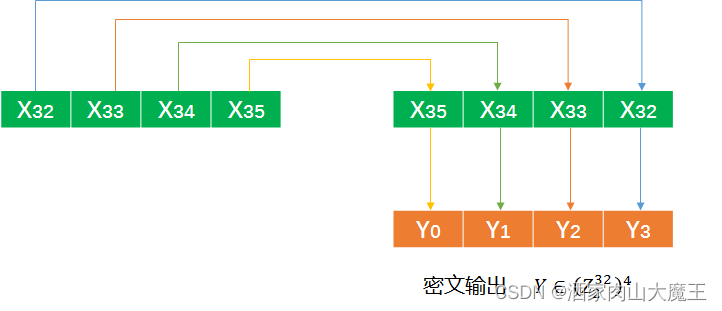
4. 解密算法

SM4算法的解密变换与加密变换结构相同，不同的仅是轮密钥的使用顺序。

解密时，使用轮密钥序 rk31,rk30,⋯,rk0rk31,rk30,⋯,rk0。

---

5. 小结

先将128比特密钥 MKMK 扩展为32个轮密钥 rkrk，再将该轮密钥与128比特明文 XX 经过轮函数进行32次迭代后，选取最后四次迭代生成的结果 X32,X33,X34,X35X32,X33,X34,X35 进行反序变换，该变换结果作为最终的密文 YY 输出。