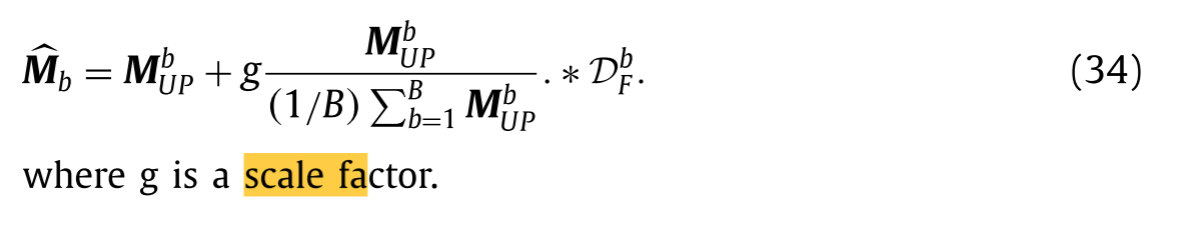Intensity mixture and band-adaptive detail fusion for pansharpening
(用于全色锐化的强度混合和波段自适应细节融合)
全色锐化的目的是通过高分辨率单通道全色(PAN)图像锐化低分辨率多光谱(MS)图像,以获得高分辨率多光谱(HRMS)图像。然而,全色图像与MS图像之间的低相关性以及MS图像各波段细节注入的不准确性是造成全色锐化中光谱和空间失真的关键问题。针对这些问题,提出了一种基于灰度混合和带自适应细节融合的全色锐化方法。为了获得与MS图像具有高相关性的混合强度图像(T)并保持PAN图像的梯度信息,通过建立T和源图像之间的强度和梯度约束来构建强度混合模型。针对模型中难以找到合适的退化滤波器的问题,利用分布对齐方法设计了滤波器估计算法。为了注入与传感器点扩展函数相匹配的细节,提出了一种波段自适应细节融合算法,将T提取的细节与MS图像提取的细节在每个波段进行融合。此外,由于MS图像中的细节比T图像中的细节少得多,因此提出了一种细节增强算法来按比例增强细节。通过将融合的细节注入到上采样的MS图像中来获得最终的HRMS图像。
介绍
遥感卫星获取的图像广泛应用于科学研究、军事侦察、工农业生产等领域。然而,由于传感器技术的限制,很难直接获得高空间分辨率的多光谱(HRMS)图像。目前的卫星通常包含两种类型的传感器。第一种是光谱传感器,其可以获得具有低空间分辨率但高光谱分辨率的多光谱(MS)图像。第二种是空间传感器,可以获得具有高空间分辨率但低光谱分辨率的全色(PAN)图像。因此,融合MS和PAN图像是克服硬件限制获得HRMS图像的最佳途径。遥感图像融合俗称全色锐化,是图像分割、分类等进一步图像处理任务的基础。在过去的几十年中,全色锐化方法发展迅速,大致分为四类:基于组件变换(CS)、多分辨率分析(MRA)、变分优化(VO)和深度学习(DL)的方法。基于CS的方法首先将上采样MS图像(UPMS)变换为不同的分量,并使用PAN图像来替代空间分量。流行的基于CS的方法包括Gram-Schmidt自适应(GSA)、主成分分析(PCA)和强度色调饱和度(IHS)。为了进一步优化空间分量,Yang等人提出了一种基于模糊逻辑和显著性度量的方法。基于CS的方法通常可以有效地获得高空间质量,但光谱质量不令人满意,特别是当源图像之间存在低分辨率时。基于MRA的方法首先将源图像分解为多个层次,然后在每个层次上进行融合。例如,轮廓波变换、拉普拉斯金字塔和加性小波变换是著名的MRA方法,它们可以获得良好的谱保真度。然而,与基于CS的方法相比,这种方法通常需要更大的计算成本,并且通常具有较差的空间分辨率。为了提高空间分辨率,提出了双边滤波亮度比例(BFLP)方法。Vivone等人在拉普拉斯金字塔中进一步采用了鲁棒技术,取得了良好的泛化性能。然而,基于MRA的方法需要进一步平衡空间和光谱质量。
基于VO的方法首先基于空间和光谱先验构建模型,然后通过特定优化算法求解该模型。为了联合收割机基于VO和MRA方法的优点,提出了基于多尺度变换的抠图模型(MMMT),提高了光谱保真度。为了改善全尺度(FS)融合结果,提出了基于全尺度回归的全色锐化注入系数,并实现了最先进的性能。针对稀疏表示在图像重构中的强大能力,提出了一种基于压缩感知的融合方法。该方法在一些数据集上取得了较好的效果,但由于字典的训练,计算代价较高。Palsson等人用循环下降和流形优化来求解降秩(RR)全色锐化模型,以及Yang等人提出了低秩模糊融合(LRFF)细节优化方法,进一步平衡融合效率和融合质量。这些方法通常比基于CS或MRA的方法获得更好的融合结果,但其性能在很大程度上取决于所构造模型的精度,其效率需要进一步提高。
基于DL的方法由于其强大的特征学习能力而在图像融合中表现出令人印象深刻的性能。Ozcelik等人提出了基于GANs的PAN图像彩色化方法(PanColorGAN),该方法可以获得较好的空间效果。为了利用其它模型的优点,Deng等人将残差网络与细节注入模型相结合,提出了FusionNet网络。Wu等人将基于VO的方法与基于DL的方法相结合,提出了VO + Net方法。 Yang等人通过提出的双流CNN增强残差信息以提高空间质量。这些方法在保持光谱和空间保真度方面表现良好,但需要大量的训练样本,具有昂贵的计算资源。
现有的全色锐化方法往往忽略了全色图像与MS图像之间的相关性,只提取全色图像的细节信息。由于MS和PAN图像之间的辐射测量差异,HRMS和PAN图像之间存在空间差异。源图像之间的低相关性实际上是导致融合结果不理想的主要因素之一。此外,注入能够匹配MS传感器的点扩展函数(PSF)的细节是具有挑战性的,因为MS图像的不同波段中的空间结构变化很大。此外,大多数全色锐化方法难以平衡融合质量和效率。针对这些问题,提出了一种基于强度混合模型和带域自适应细节融合算法的全色锐化方法。
强度混合模型被设计为混合原始MS图像的强度分量(Iorg)和PAN图像的空间信息,从而获得与MS图像具有高相关性但不丢失PAN图像的梯度信息的混合强度图像(T)。然后用T代替PAN图像,从而增强待融合图像之间的相关性。为此,建立了降质后的T和Iorg之间的强度一致性约束以及T和PAN图像之间的梯度约束。针对退化滤波器难以获得的问题,提出了一种基于分布对齐的滤波器估计算法,以提高退化滤波器的精度。
在波段自适应细节融合算法中,本研究将从T提取的细节与UPMS图像中提取的细节进行融合,以获得每个MS波段的精确细节。为了更好地匹配细节和传感器的PSF,通过应用与MS传感器的调制传递函数(MTF)匹配的高斯滤波器来获得UP MS图像中的细节。由于UP MS图像中的细节比T图像中的细节少得多,提出了一种细节增强算法,按比例增强图像中的细节。通过将带自适应细节注入到UP MS图像中来获得最终的HRMS图像。
贡献
1)提出了一种基于亮度混合模型和带域自适应细节融合算法的全色锐化方法,该方法能有效地获得高光谱和空间质量。
2)为了增强源图像之间的相关性,通过建立退化T与Iorg之间的强度约束和T与PAN图像之间的梯度约束,设计了一种强度混合模型。此外,提出了一种滤波估计算法,以同时优化模型内退化的滤波器。
3)为了提高各波段注入细节的准确性,提出了一种波段自适应细节融合算法,将T波段和MS波段的细节进行融合。同时,提出了一种细节增强算法,对MS图像进行细节增强,以达到更好的细节融合效果。
相关工作
细节注入模型以其灵活性和可扩展性一直是全色锐化中的热门模型。将具有B个波段的MS图像表示为M ∈
R
l
×
w
×
B
R^{l×w ×B}
Rl×w×B,M的上采样形式MUP ∈
R
L
×
W
×
B
R^{L ×W ×B}
RL×W×B,且PAN图像为P ∈
R
L
×
W
R^{L ×W}
RL×W,其中l × w和L × W分别表示M和P的大小,则基于细节注入模型的传统全色锐化方法统一表示为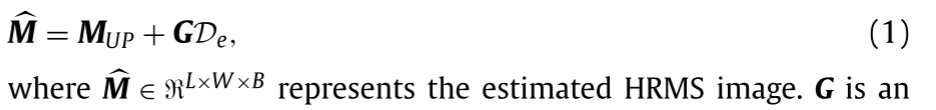
G是注入增益,De表示注入细节。基于CS和MRA的方法的区别主要在于De的提取方式。对于基于CS的方法,De可通过以下方式获得

其中Phist表示直方图与IUP匹配之后的PAN图像,IUP表示MUP的强度分量。强度(IUP)通常通过MUP的谱带的加权和获得,其表示如下:
其中,b表示变量的第b个波段,
M
b
M^b
MbUP表示上采样MS图像的第b个波段,αb表示用于获得强度分量的线性系数的第b个波段。
对于基于MRA的方法,De通过下式获得:
其中PL表示退化的PAN图像,其可以通过对P应用低通滤波器H来获得。
为了保持更好的光谱和空间保真度,基于VO的方法吸引了越来越多的关注,其将融合过程视为模型优化问题。具体而言,这种方法基于原始MS、PAN和理想HRMS图像之间的关系来构造能量函数。能量函数主要由两个先验项组成。第一个是光谱保真度项,第二个是空间保真度项,可表示如下: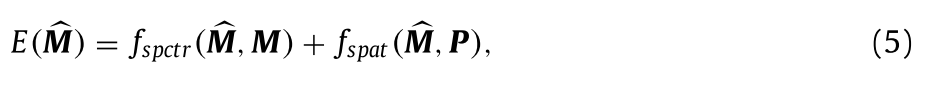
其中,fspctr(·)和fspat(·)分别表示光谱保真度函数和空间保真度函数。fspctr(·)建立以下光谱关系^M和M基于先验知识。也就是说,M可被视为 ^M的模糊和抽取版本而fspat(·)则基于先验建立 ^M和P之间的空间关系。就像是模糊的和简化的版本而f spat(·)则建立M之间的空间关系以及基于先验的P。因此,P被视为以下频带的加权和 ^M。因此,公式(5)中的能量函数可以重新定义如下:
其中λ表示惩罚参数,D表示下采样矩阵,并且C表示线性组合矩阵。找到公式(6)的优化解,我们可以得到^M。然而,公式(1)中的细节注入模型和公式(6)中的基于VO的模型都认为仅从PAN图像中提取细节,忽略了MS图像中存在而PAN图像中不存在的本征细节。不准确的细节提取可能导致频谱和空间失真。
方法
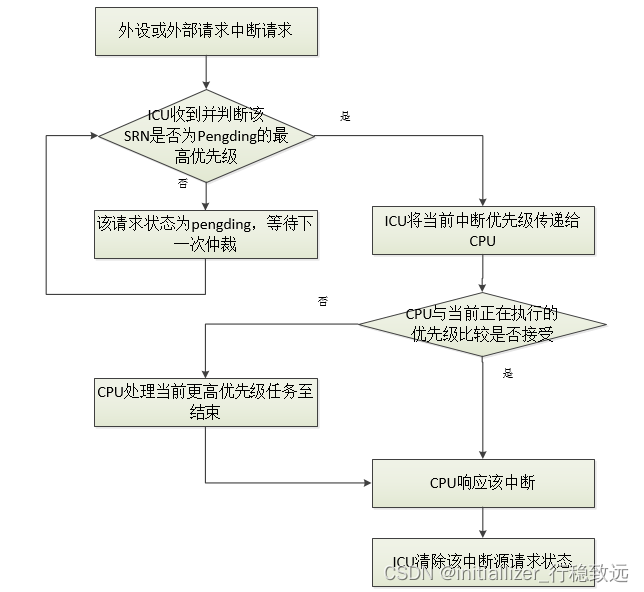
本文着眼于提高待融合图像之间的相关性和带域自适应地优化细节,提出了一种基于亮度混合和带域自适应细节融合的全色锐化方法,如图1所示。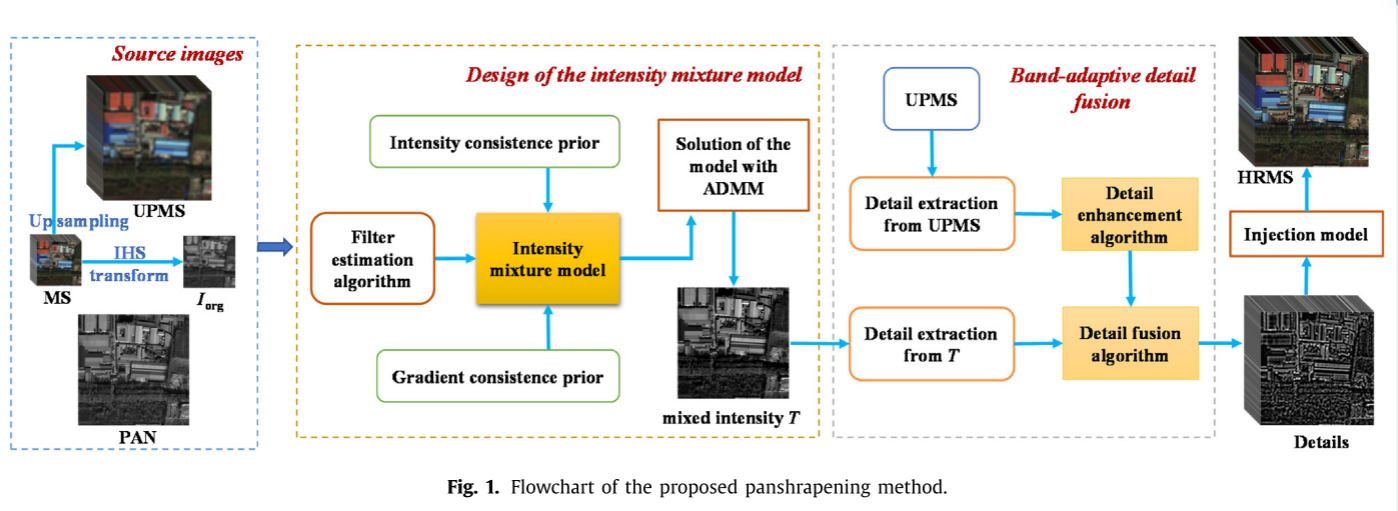
Iorg和P被用作强度混合模型的输入。该模型基于亮度一致性先验建立退化图像T与Iorg之间的亮度约束,基于梯度一致性先验建立退化图像T与源图像之间的梯度约束。此外,提出了一种滤波器估计算法,以获得合适的滤波器用于降低模型中的T。利用交替方向乘子法(ADMM)对模型进行求解,得到T。为了获得与MS传感器的PSF相匹配的精确细节,首先通过MTF匹配高斯滤波器提取UP MS图像的细节,然后通过细节增强算法进行增强。然后,利用细节融合算法将增强后的UP MS细节与T中的细节进行融合。最终使用细节注入模型获得HR MS图像。
Intensity mixture model
Model construction
频谱保真度约束是根据以下假设定义的:M可被视为的抽取和模糊版本^M,模糊函数应为类高斯滤波器。因此,约束通常设计为
其中^Mb和Mb分别表示估计的HRMS图像和原始MS图像的第b个波段, ^M或M可通过将
M
b
M^b
MbUP替换为 ^Mb或者Mb根据式(3)。
为了保持波段之间的固有相干性,最好对^M所有波段执行统一的高斯滤波器HG 。因此,用HG 代替Hb ,并将(3)和(7)结合在一起,我们可以推导出如下公式:
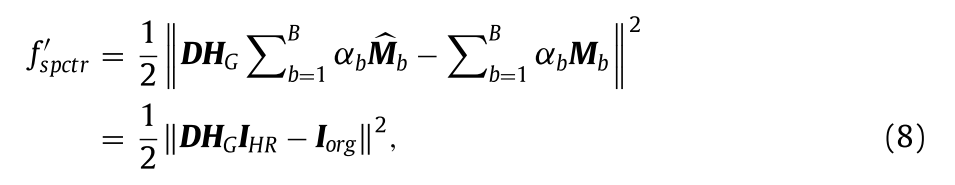
其中IHR表示的强度分量^M。为了获得与M具有高相关性的T,合理地假设T应当接近IHR。强度分量M。为了获得与M具有高相关性的T,合理地假设T应当接近IHR。为此,本文提出了一种强度一致先验;也就是说,Iorg可以被认为是T的模糊和抽取版本。T需要满足的另一个要求是T不应该丢失P的梯度信息。因此,组合强度一致性约束和梯度一致性约束的模型可以表示为
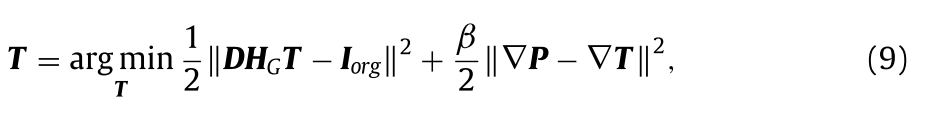
其中▽表示拉普拉斯算子,β表示罚参数。由于P的梯度信息的学习可能会导致T与Iorg之间的相关性出现偏差,因此提出一种降尺度梯度约束来进一步增强T与Iorg之间的相关性。表示S = DHGT,我们将缩小比例的梯度约束定义如下:
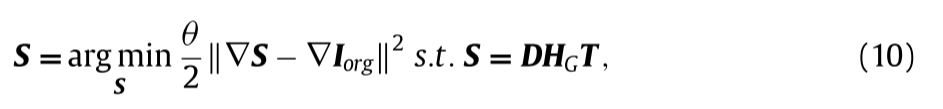
其中θ表示罚参数。为了保证梯度图的稀疏性和减少伪影,模型中引入了全变分(TV)项。结合(9)和(10)中的约束,强度混合模型被表示为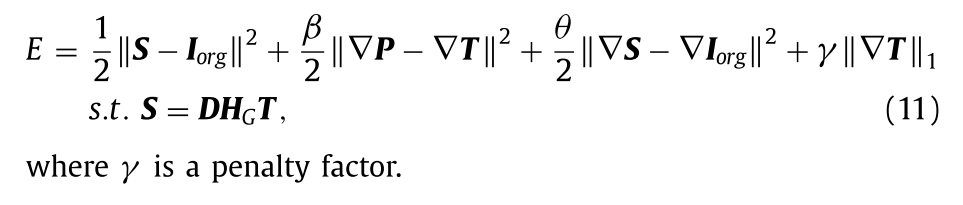
Filter estimation algorithm
在式(11)表示的模型中,HG仍然是不确定的,但可以通过观测数据进行估计。如果已知理想T,则可通过以下公式确定HG: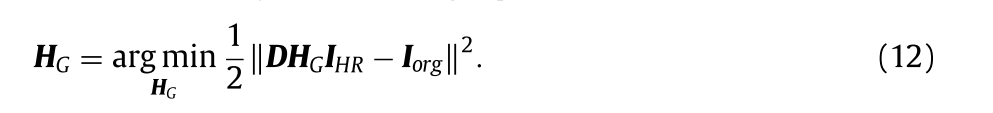
由于空域图像滤波是一个卷积过程,给模型求解带来不便,将HG变换到频域,将卷积转换为矩阵之间的内积。HG(x,y)的频域表示为
其中,Dt(U,V)表示距频率矩形中心的距离,σ表示标准差。将快速傅里叶变换(FFT)表示为F(·),将逆FFT(IFFT)表示为
F
−
1
F^{−1}
F−1(·),我们可以得到: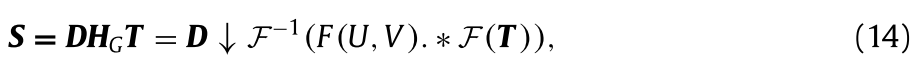
其中D ↓表示下采样操作。确定HG的关键是找到一个合适的分布参数σ,使S与Iorg一致。采用相关函数来表示S和Iorg之间的相似性,目标是最大化它们之间的相关性。因此,(13)中的最佳σ可通过下式获得:
其中corr(·)表示相关函数,σ * 表示最优σ。初始化σ为σ0,步长为l,迭代计算式(15)中的相关性,直到相关性达到最大值,得到σ *。详细算法如算法1所示。

为了说明滤波估计算法的有效性,图2显示了不同σ值下的相关曲线。测试图像来自IKONOS数据集。
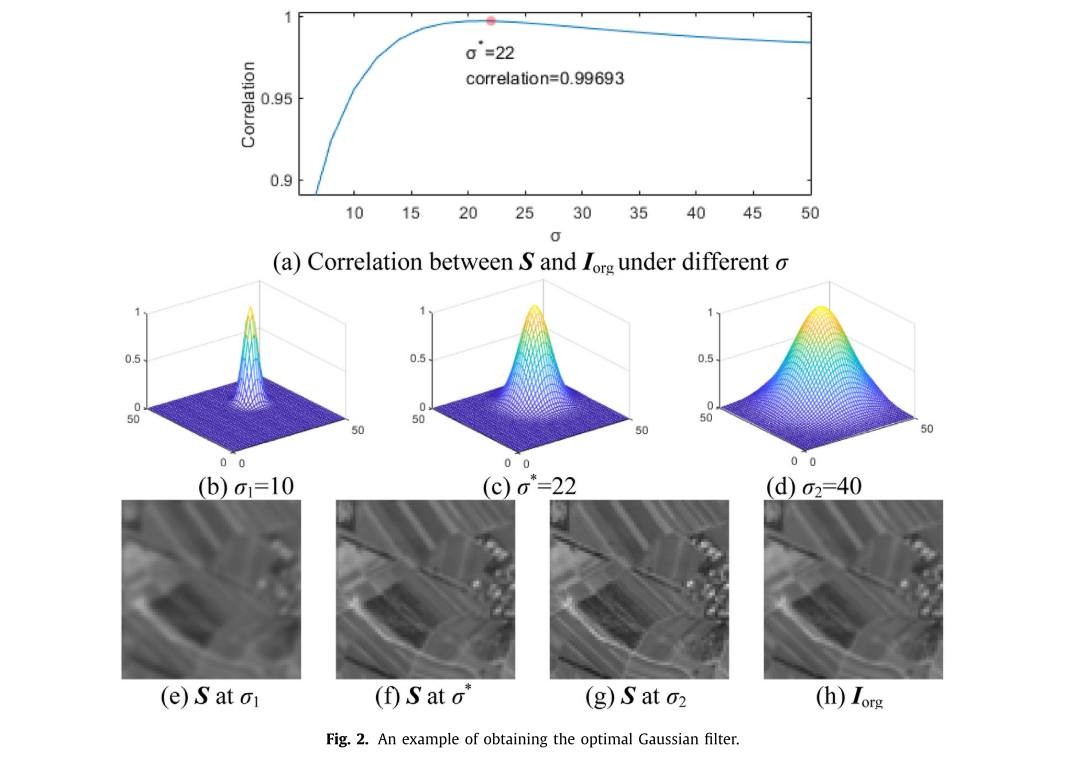
从图中可以看出,当最优分布σ *= 22时,S与Iorg的最大相关性几乎为1。不同σ值下的滤波器传递函数透视图见图2(b)-(d)。这里选择小于σ * 的σ1 = 10和大于σ * 的σ2 = 40进行比较,以便更直观地区分滤波结果。图2(e)-(h)显示了(14)在不同σ值下获得的不同S图像和Iorg图像。在这里,我们可以看到,在σ * 分布上生成的S图像可以最好地与Iorg对齐,这进一步验证了估计滤波器的有效性。
从(9)和(12)中,我们可以观察到T和HG是相互依赖的。通过固定一个变量并更新另一个变量,我们可以通过ADMM优化这两个变量。
The solution
为了更简单地求解,表示R = HGT,Q = ▽T,则S = DR,并且(11)的增广拉格朗日函数表示为:
Updating R
固定其他变量,R的更新是一个凸优化问题,可以通过将公式(16)中R的偏偏差设为0来获得;即,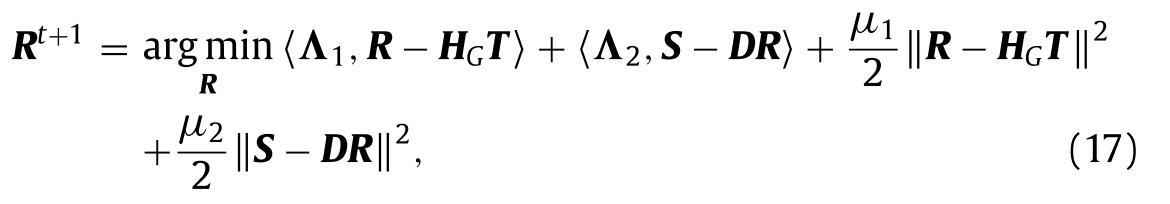
因此,R的t + 1步长由下式获得: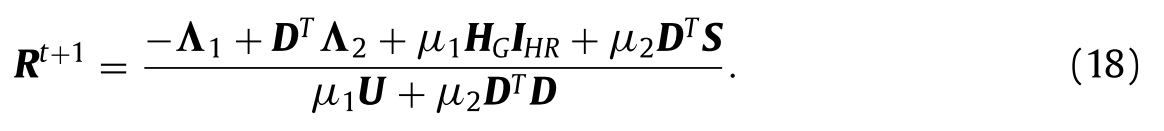
其中U表示单位矩阵,上标T表示转置算子。
Updating S
使用与更新R相同的方法,并将S的偏偏差设置为0,我们可以获得如下偏差结果: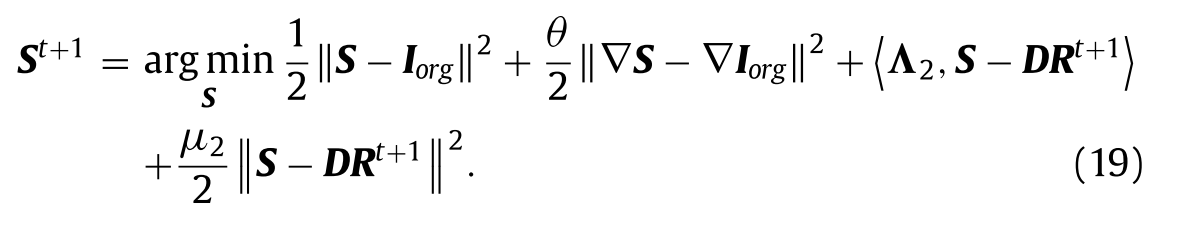
为了提高效率,采用了FFT和IFFT。因此,利用更新后的
R
t
+
1
R^{t +1}
Rt+1,S的t + 1步长由下式获得:
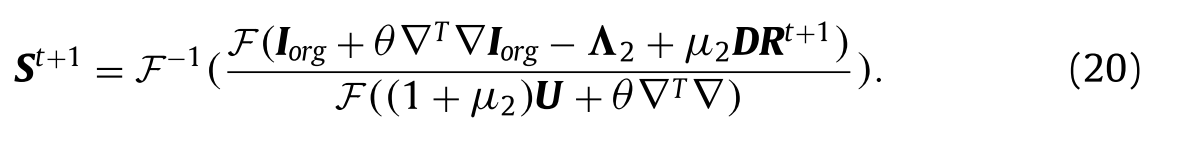
Updating T
类似于更新S,固定
R
t
+
1
R^{t +1}
Rt+1并设置T的偏偏差为0的方法,我们得到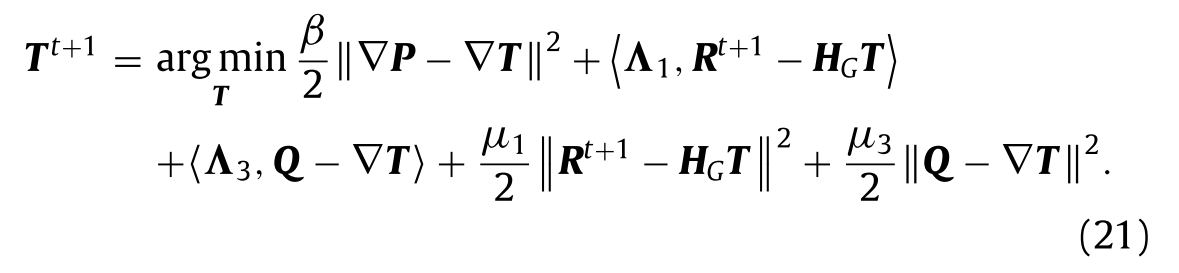
这里,我们也使用FFT和IFFT来提高效率,并且IHR的t + 1步由下式获得: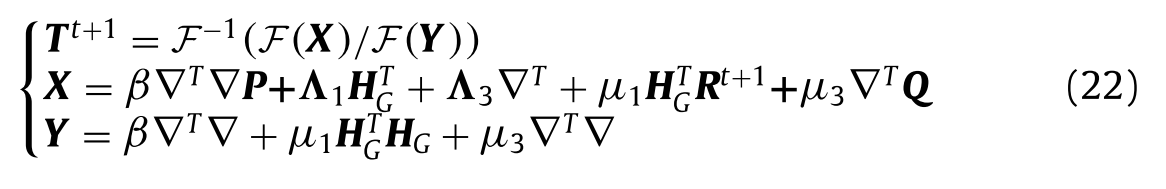
Updating Q
固定其他变量,我们可以通过最小化能量函数来获得Q的更新,如下所示:
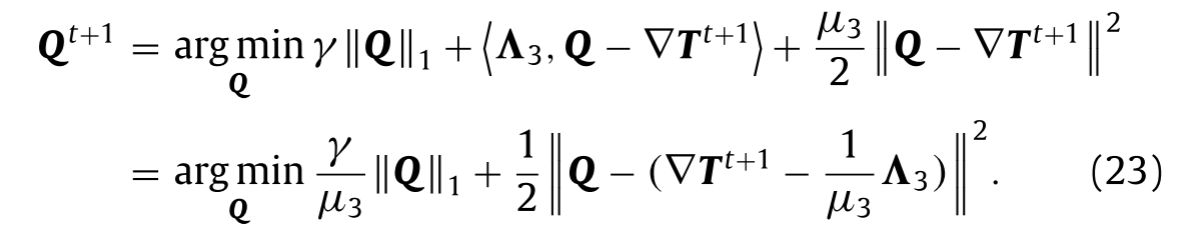
使用软阈值策略,(23)可以通过下式有效求解
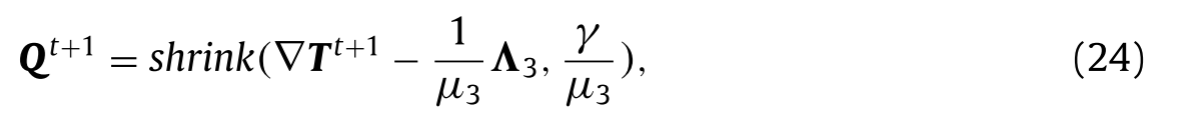
其中
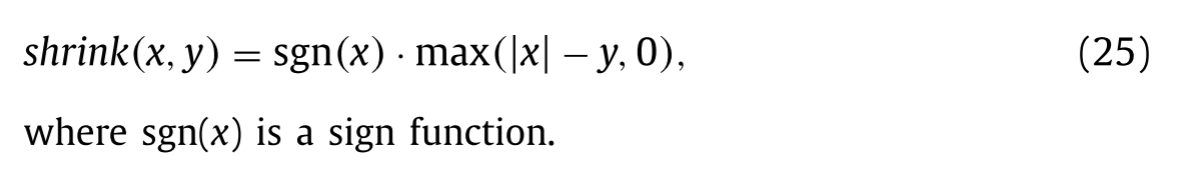
Updating Lagrangian multipliers
拉格朗日乘子Λ1、Λ2和Λ3的最大值可以通过梯度上升法获得如下: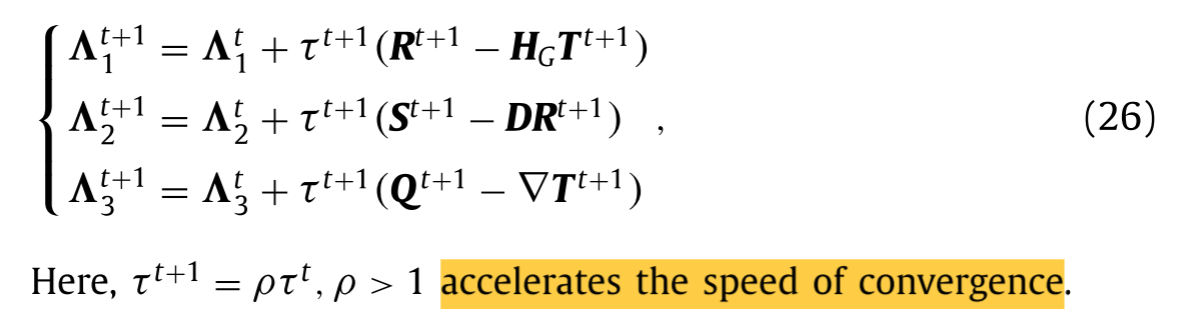
总之,在算法2中示出了强度混合模型的整体解。在迭代过程期间,HG同时用算法1更新,当相对误差满足停止条件时得到最终T;即,
Band-adaptive detail fusion

给定MS波段的不同空间特性,仍然难以将匹配MS传感器的PSF的精确细节注入MS图像的每个波段。MS传感器的MTF可以由制造商获得,然后在MS图像上应用MTF匹配高斯滤波器(HM)。所获得的细节也应与MS传感器的PSF匹配。通过在UPMS图像上应用HM获得的细节表示为
其中
D
b
D^b
DbM表示从UPMS图像提取的第b个波段细节。对于每个波段,将DT与
D
b
D^b
DbM融合可以更好地匹配MS传感器的MTF。但
D
b
D^b
DbM中的像素值比DT中的像素值小得多,因为UPMS图像包含的细节很少。为了更好地演示要融合的细节,图3中示出了所提取细节的示例。
为简单起见,我们只展示了MUP的第一个谱带的细节,如图3(b)所示,从中我们可以看出
D
b
D^b
DbM远小于DT。简单地将DT与
D
b
D^b
DbM融合会导致一些细节信息的丢失。因此,我们希望用一个比例因子(ωb)将
D
b
D^b
DbM按比例增强到DT的水平,以避免细节融合过程中的空间损失。为了实现这一目标,设计了一个模型来约束增强的
D
b
D^b
DbM。也就是说,ωb
D
b
D^b
DbM接近于DT,如下所示: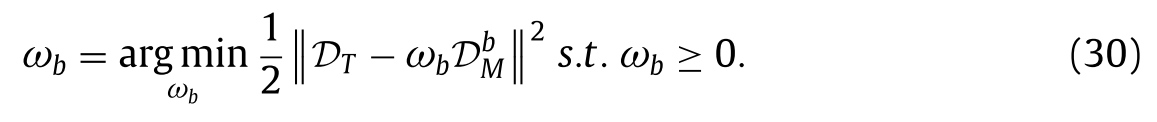
为了求解模型(30),采用拉格朗日乘子法和梯度下降法,我们可以获得如下解: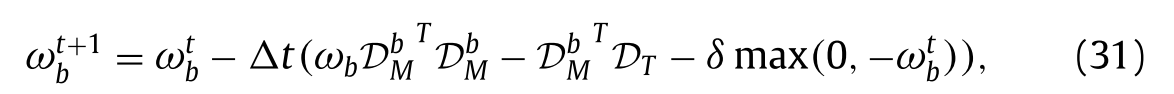
其中△t为步长,δ为罚参数。当
ω
t
+
1
ω^{t+1}
ωt+1b与
ω
t
ω^t
ωtb之间的误差足够小时,迭代将停止。
将ωb
D
b
D^b
DbM表示为
D
b
D^b
DbE,我们可以融合DT和
D
b
D^b
DbE,以获得更好地匹配传感器PSF的细节。细节融合算法设计如下: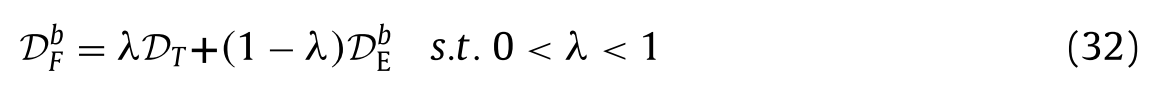
其中λ是权重系数,
D
b
D^b
DbF表示融合细节。由于细节的准确性受到源图像之间的相关性(表示为c)的影响,因此λ应与c呈正相关。为了将λ限制在一个更合理的范围内,本文基于Sigmoid函数定义λ如下: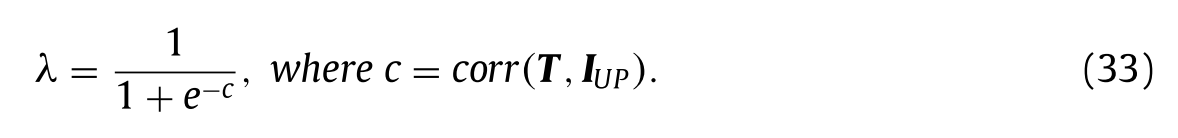
将(33)中的λ代入(32)中,得到带自适应细节。使用注射模型,可以通过以下方式获得最终HRMS图像: