✅作者简介：CSDN内容合伙人、信息安全专业在校大学生🏆
🔥系列专栏 ：课设-密码学课设-RSA
📃新人博主 ：欢迎点赞收藏关注，会回访！
💬舞台再大，你不上台，永远是个观众。平台再好，你不参与，永远是局外人。能力再大，你不行动，只能看别人成功！没有人会关心你付出过多少努力，撑得累不累，摔得痛不痛，他们只会看你最后站在什么位置，然后羡慕或鄙夷。

---

格式比较乱，因为是word转makrdown的,原谅我手懒

必 做

一、实验题目

密码学破解课程-HASH

二、实验要求

掌握Hash、MD4、MD5、SHA1等概念
孰练使用HASH工具
学习Hash算法在信息安全方面的应用

三、实验步骤

1、使用HashCale软件进行文件校验
1.1登录到操作系统
1.2进入在实验目录(D:\2、网络攻防\2、网络入侵\29密码破解课程\9.口令破解-01HASH基础实验\口令破解-01HASH基础实脸),将实验工具压缩包“口令破解-01HASH基础实验.rar”文件“解压到当前文件夹，进入解压后的目录，找到HashCale工具,双击HashCale.exe, 如下图所示：

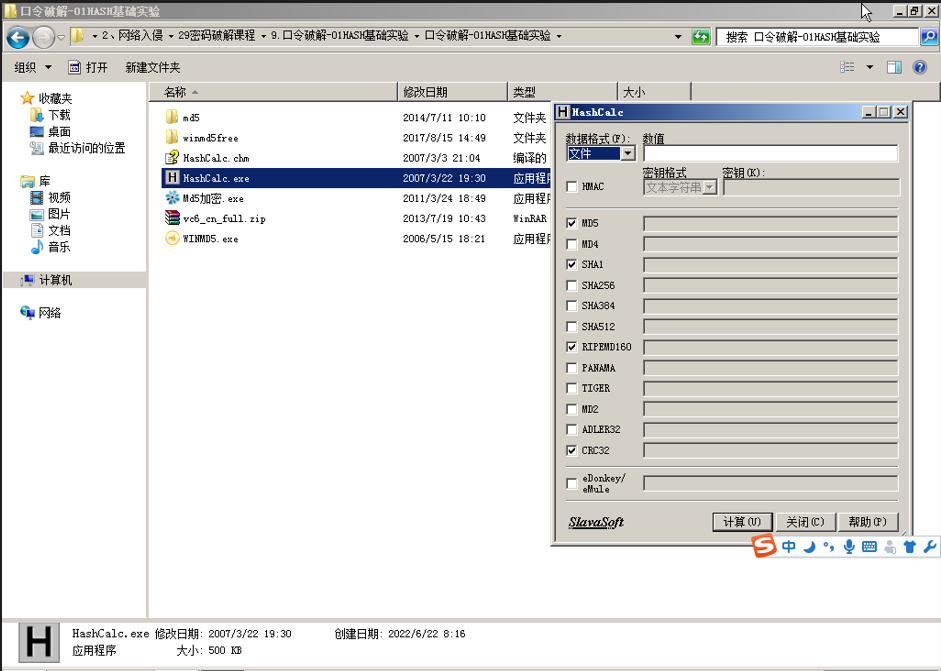
只需将文件拖放进HASHCALE的窗口即可。拖动此目录中的WINMD5.exe文件到数值窗口中。如下图所示:

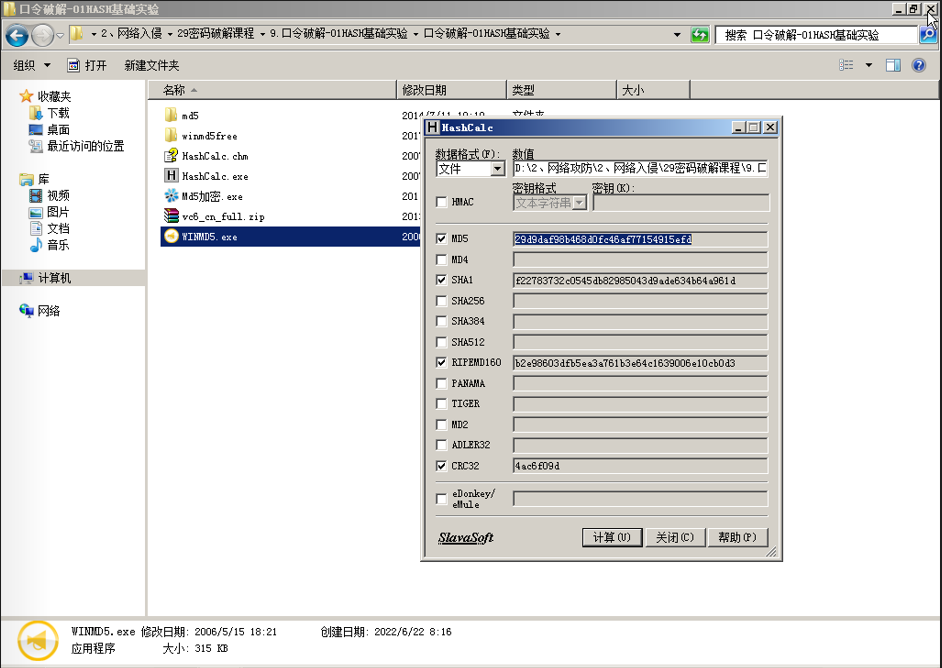
2、使用WinMd5软件计算出MD5校验值
2.1进入解压后的目录下的winmd5free子目录,双击打开WinMD5.exe，如下图所示：

2.2只需将文件拖放进WinM1D5的窗口即可。拖动上级目录中的HashCalc.exe文件到窗口中。如图所示：

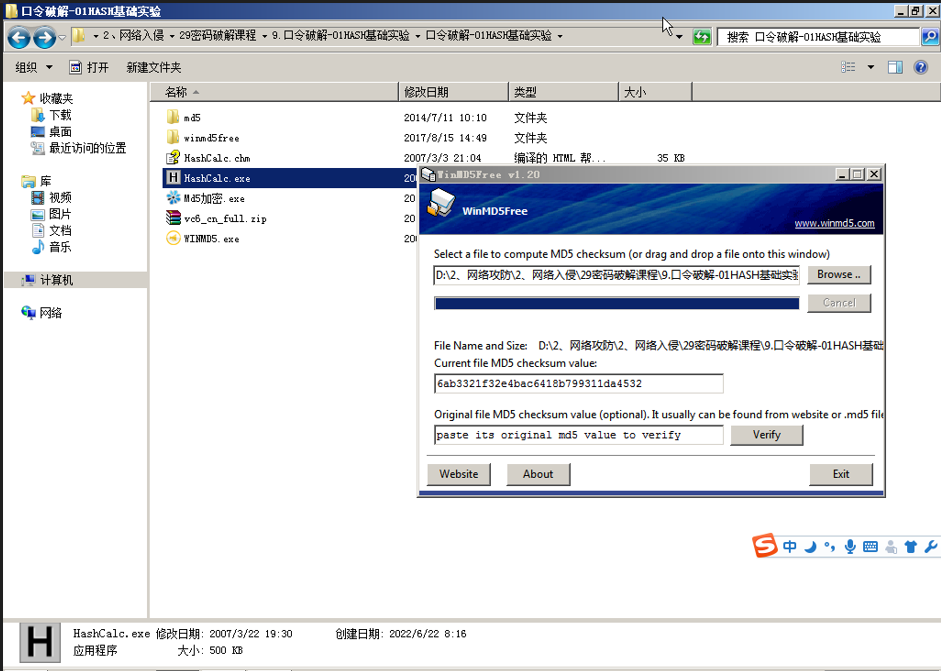
3、针对于数字串文件进行HASH
3.1双击目录下的“MD5加密.exe”软件
3.2在“密码明文”处输入admin,即可获得所想得到的加密信息,如下图所示

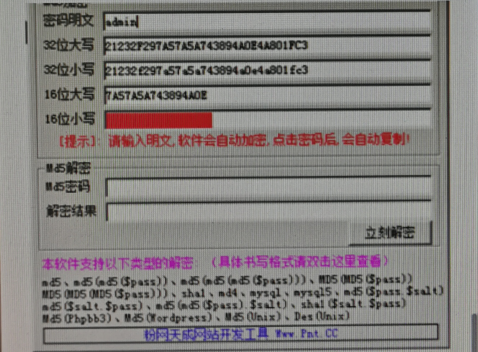
4、在Windows_Server 2008创建简单的网站,计算MD5散列值
4.1打开“开始”>“管理工具”>“IIS服务”如下图所示:

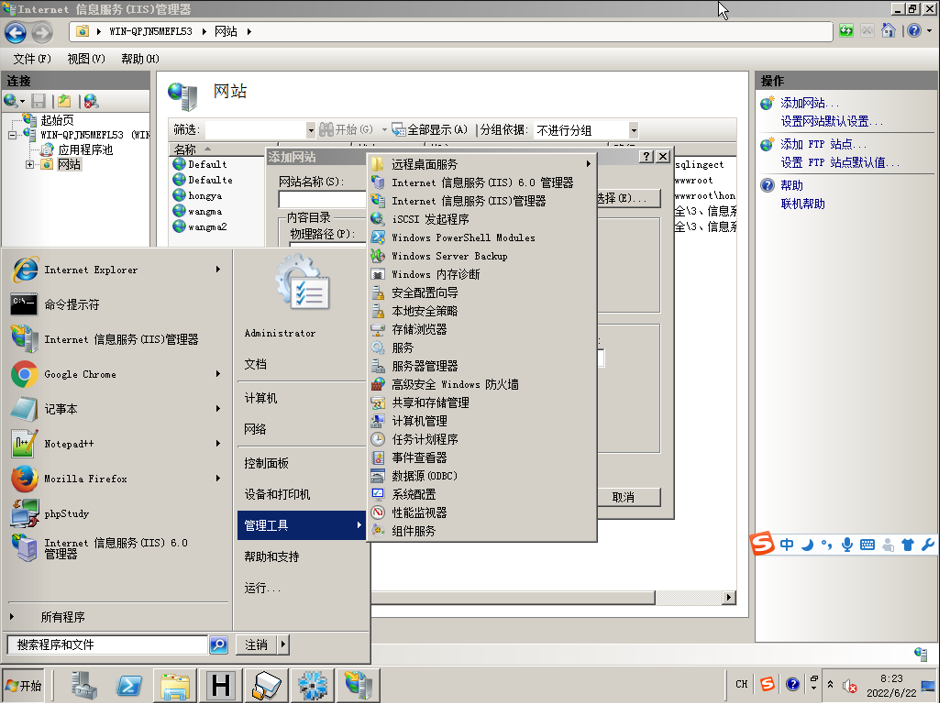
4.2打开IIS界面。右键网站，选择添加网站
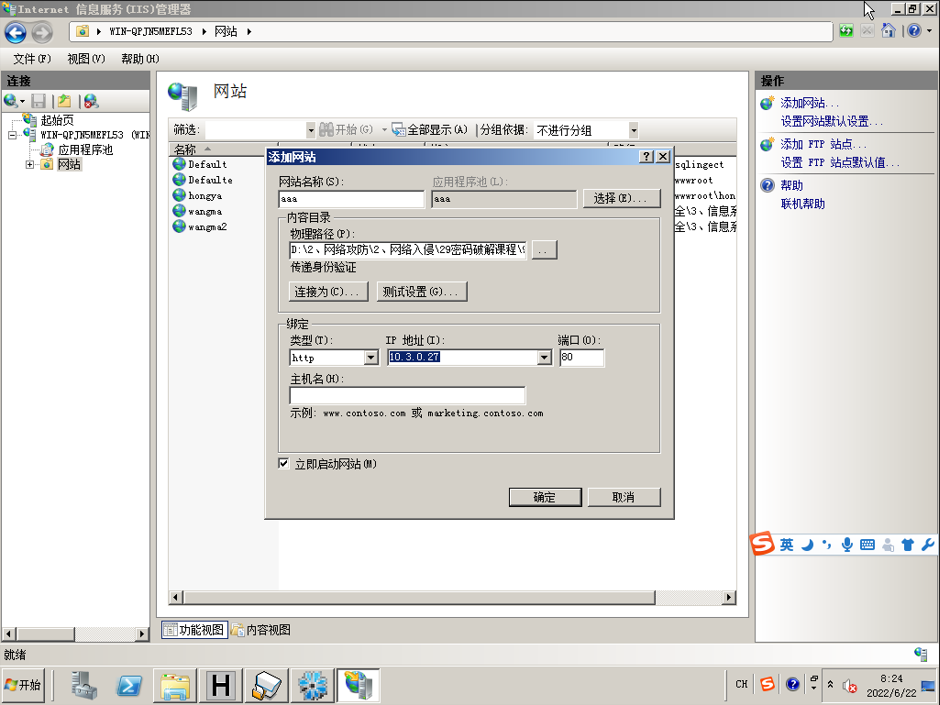
4.3进入添加网站界面,先可网站的名字,这里输入的是“aaa”，用来识别该网站。物理路径选择实验工具路径下的md5文件的位置。IP地址输入操作机自身的IP。最后点击“确定”。

4.4现在链接到我们创建的IIS网站，示例操作机IP访问地址为:http://100.100.0.9/.
4.5显示页面的内容,这里面我们在输入框中分别添加“111”,密码:“ 111”然后点击提交按钮。

四、运行结果

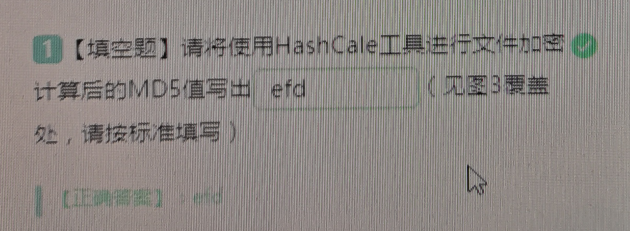
图 1 步骤一运行结果

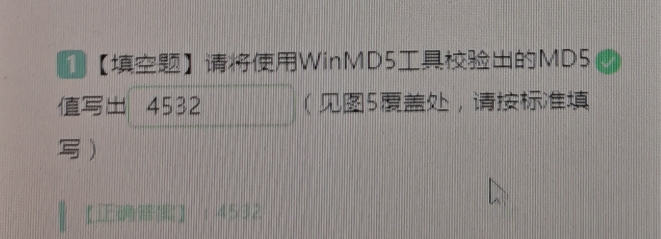
图 2 步骤二运行结果

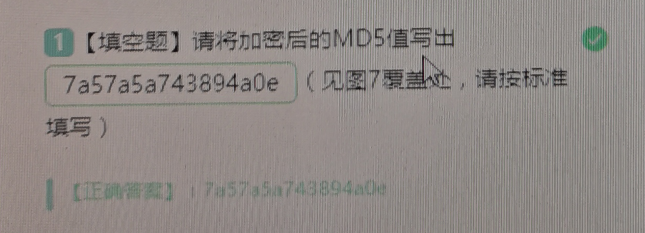
图 3 步骤三运行结果

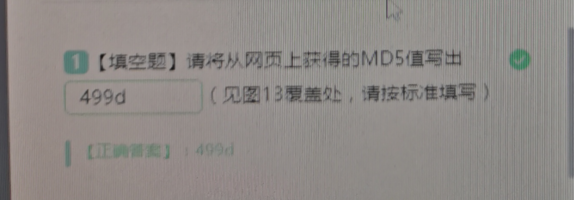
图 4 步骤四运行结果

图 5 综合测验（一）

图 6 综合测验（二）

选 做

一、设计题目

第五题 —— RSA攻击

二、设计要求

1）对于RSA的攻击有共模攻击，广播攻击、低加密指数等，调研更多攻击如低解密指数攻击（Wiener攻击）、基于格的攻击、Coppersmith短填充攻击等，选择至少4种攻击，模拟攻击过程，并给出结果；
2）要求RSA的模512比特以上

三、系统设计

1. RSA加密原理：

1. 任意选取两个大素数,计算
2. 任意选取一个大整数e, 满足,整数e用作公钥
3. 确定私钥d, 满足
4. 若M为待加密对象，
5. 解密

2. 扩展欧几里得算法求逆元

若a与b互质，那么, 即 ax + by = 1, 于是 by = (-x)a+1
也即：by=1(mod a)，于是y即为b在模a意义下的乘法逆元。在欧几里得算法中，可以把过程写的更清晰一些：（仍以为例）

带入得：

于是，据此可以构建一个表格来计算乘法逆元

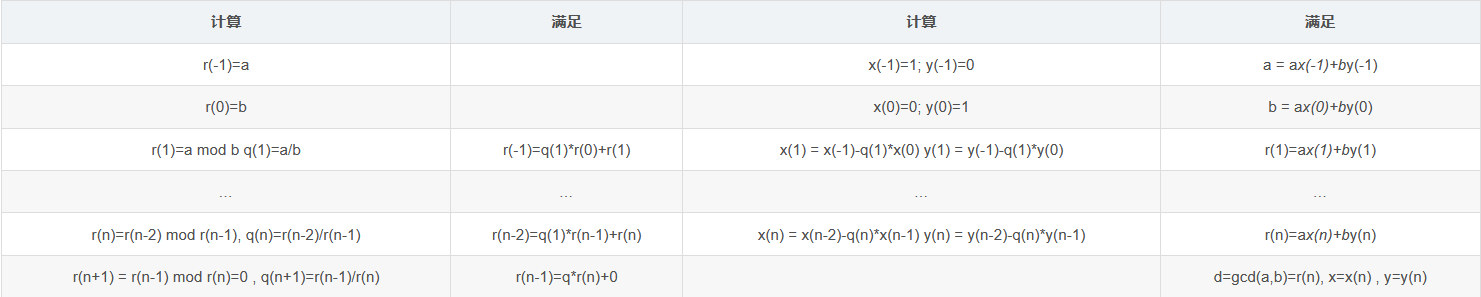
图 7 计算乘法逆元表格

图 8 实现的核心代码

3. 快速幂指数算法

在RSA中，加、解密过程都是要求某个整数的整数次幂后再取模。大多时候，这两个整数都会比较大，这时候直接按含义来进行计算时得到的中间结果会超出计算机所允许的整数取值范围（例如计算66^77，这还是比较小的）所以需要一种算法较快地计算 a^p (mod n) 快速幂算法能帮我们算出指数非常大的幂，传统的求幂算法之所以时间复杂度非常高（为O(指数n)），就是因为当指数n非常大的时候，需要执行的循环操作次数也非常大。所以我们快速幂算法的核心思想就是，将指数二进制展开，每一步都把指数分成两半，而相应的底数做平方运算。这样不仅能把非常大的指数给不断变小，所需要执行的循环次数也变小，而最后表示的结果却一直不会变。实现的流程图如下：

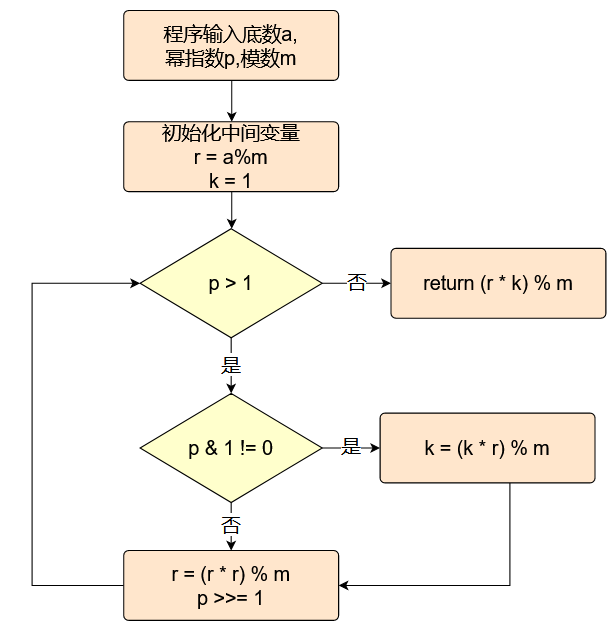
图 9 快速幂指数流程图

4. 共模攻击原理及代码实现

1、共模攻击原理

1. 如果在 RSA 的使用中使用了相同的模 n 对相同的明文 m 进行了加密，那么就可以在不分解 n 的情况下还原出明文 m 的值。即：

3. 此时不需要分解 n，不需要求解私钥，如果两个加密指数互素，就可以通过共模攻击在两个密文和公钥被嗅探到的情况下还原出明文 m 的值，过程如下：

4. 首先两个加密质数互质，则（c1, c2）= 1，即存在s1, s2 使s1e1+s2e2=1

5. 将4）表达式带入2）中，即可得到

2、共模攻击代码实现
所以程序首先输出模数n, 两个加密指数e1,e2和两个对应的密文c1,c2，然后利用扩展欧几里得算法求得e1,e2的相应逆元r和s，考虑到r和s一正一负，所以假设当r是负数时，求C1在模数n下的逆元，即可实现对r的正数化，s是负数的情况同理。核心代码实现如下：

图 10 共模攻击核心代码

5. 低加密指数攻击原理及代码实现

1、低加密指数原理
RSA的加密为。当加密指数e很小，N很大时，M可能小于N，此时有两种方式。一直接对密文C开e次方，或者M = KN + C，循环遍历可能的K值，直到KN + C 开e次方出现整数即可。
2、低加密指数攻击代码实现
该代码中的gmpy2.iroot()函数主要用于判断开e次方根是否为整数。

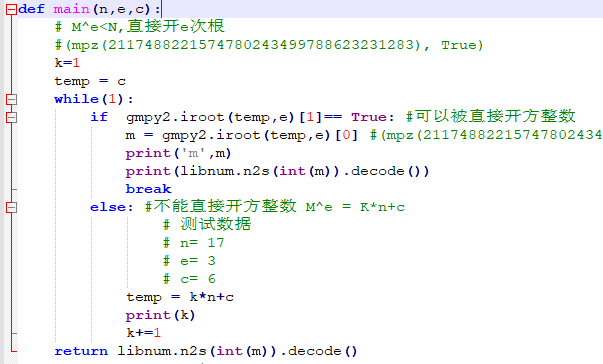
图 11 低加密指数攻击核心代码

6. 低加密指数广播攻击原理及代码实现

1、低加密指数广播攻击原理
爱丽丝需要发送同一条消息m给鲍伯、卡罗尔和戴夫。且三位接收者的公钥为(N,3),(N2,3),(N3,3)。即公钥指数都为3，公钥模数各不相同。且消息不填充。则

攻击者截取三段密文C1,C2,C3，将如下式子利用中国剩余定理可得到明文结果M。
2、低加密指数广播攻击代码实现
程序首先将得到不同的C和N存放到相应的列表中，然后利用中国剩余定理构造表达式，求出表达式。然后直接对密文C开e次方，或者M = KN + C，循环遍历可能的K值，直到KN + C 开e次方出现整数即可。

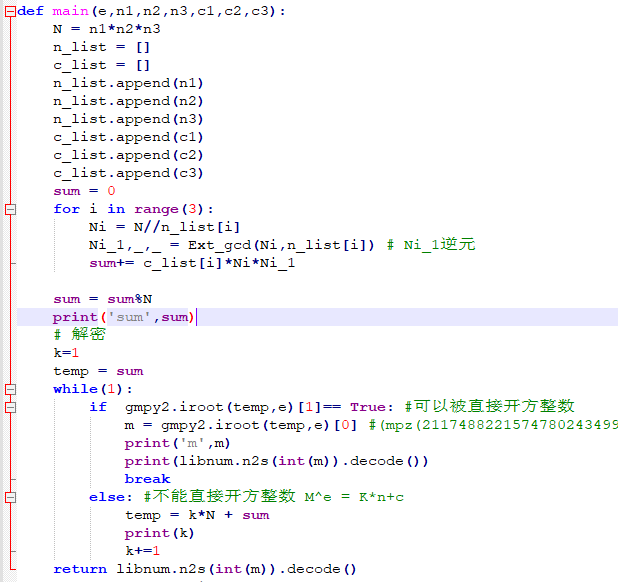
图 12 低加密指数广播攻击核心代码

7. 低解密指数攻击（Wiener攻击）原理及代码实现

1、Wiener攻击原理
与低加密指数相同，低解密指数可以加快解密的过程，但是也带来了安全问题。Wiener 表示如果满足：
那么一种基于连分数(一个数论当中的问题)的特殊攻击类型就可以危害 RSA 的安全。此时需要满足：p < q < 2p。如果满足上述条件，通过 Wiener Attack 可以在多项式时间中分解 n，思路如下：

2. 因为p, q 非常大，所以p*q >> p + q; 所以

3. 因为 所以

4. 上式两边同除_ _可得

5. 因为 所以上式子将替换为n，可得：_

6. 同样是一个很大的数，所以略大于。为啥要这么写呢？因为e和n我们是知道的，所以我们需要计算的连分数展开，依次算出这个分数的每一个渐进分数，wiener证明了，该攻击能精确的覆盖

2、Wiener攻击代码实现
程序首先输入模数n，加密指数e, 和密文c, 然后求出e/n的连分数展开，进而逆向推导算出每一个渐进分数，通过d, k循环遍历渐进分数，使得(ed -1)%k得到整数解，此时便得到了 的值，为(ed -1)//k。此时我们知道了p + q，也知道了p * q，进而利用韦达定理可求出p和q的具体值，进而破解了d，破解了RSA。实现的核心代码如下：

图 13 Wiener攻击核心代码

8. Dp泄露攻击原理及代码实现

1、Dp泄露攻击原理
dp是什么？, 当Dp泄露时，我们还知道模数n, 加密指数e, 密文c, 此时根据这四个值，可破解RSA。原理如下：

1. 因为 所以，
2. 两边同时乘加密指数e可得
3. 因为 所以
4. 将3）带入2）中可得到
5. 化解得到
6. 假设, 所以
7. 因为 所以 带入6）得到
8. 因为 ，所以只需在（0，e）的范围内，遍历X的不同取值，直到p - 1 为整数解时，该解即为p-1。
9. 进而可求得p, q, d, m

2、Dp泄露攻击代码实现
程序首先输入模数n, 加密指数e, 密文c, 和被泄露的dp，然后在(0，e)内穷举X可能出现的值，直到e*dp mod（X）为整数解时，跳出遍历，此时的值即为要求的p,进而破解了该RSA。实现的核心代码如下：

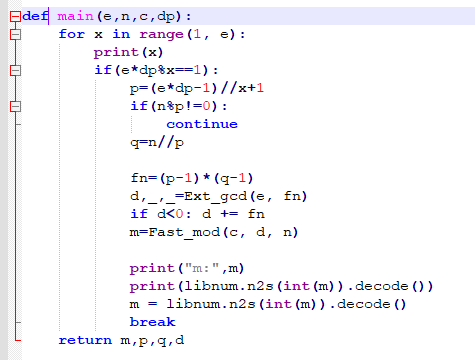
图 14 Dp泄露攻击的核心代码

9. 系统模块划分及界面设计

系统模块划分如下：

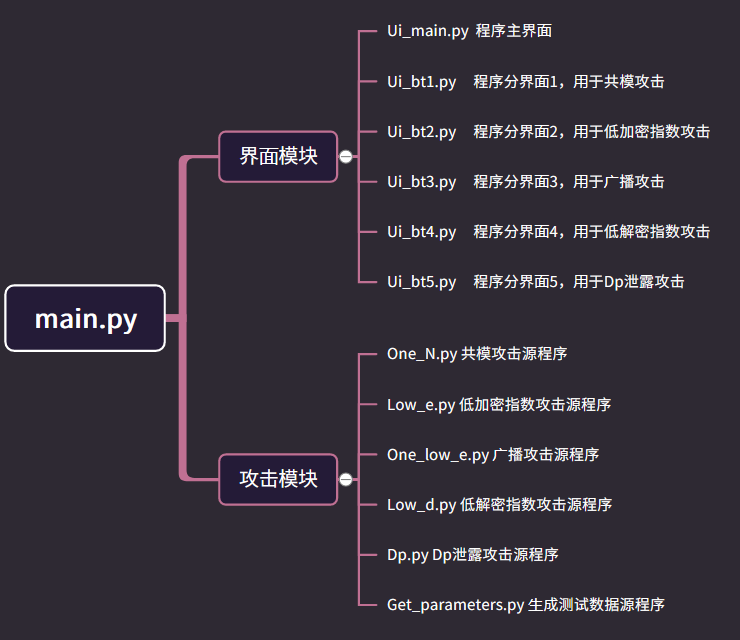
图 15 软件设计总流程图
界面设计采用Qt Designer ，五个界面的源文件分别为bt1.ui，bt2.ui，bt3.ui，bt4.ui，bt5.ui，main.ui 。软件的主界面如下图：

图 16 软件的主界面

四、运行结果

为方便测试，在附件中的Get_parameters.py 程序中，我设计了自动生成RSA相应参数的代码，方便后续的测试。程序只需要直接运行即可。

图 17 测试数据生成源代码
1、共模攻击测试

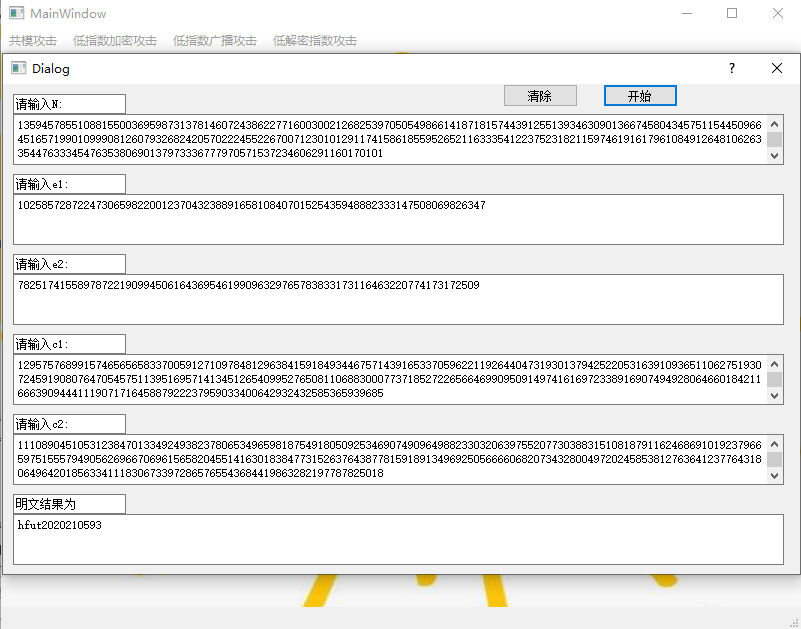
图 18 共模攻击测试1

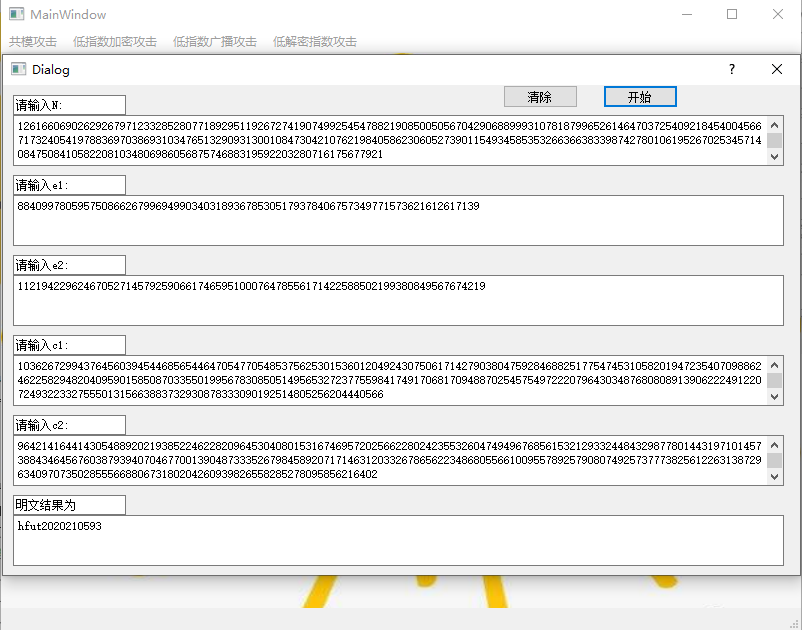
图 19 共模攻击测试2

2、低加密指数攻击测试

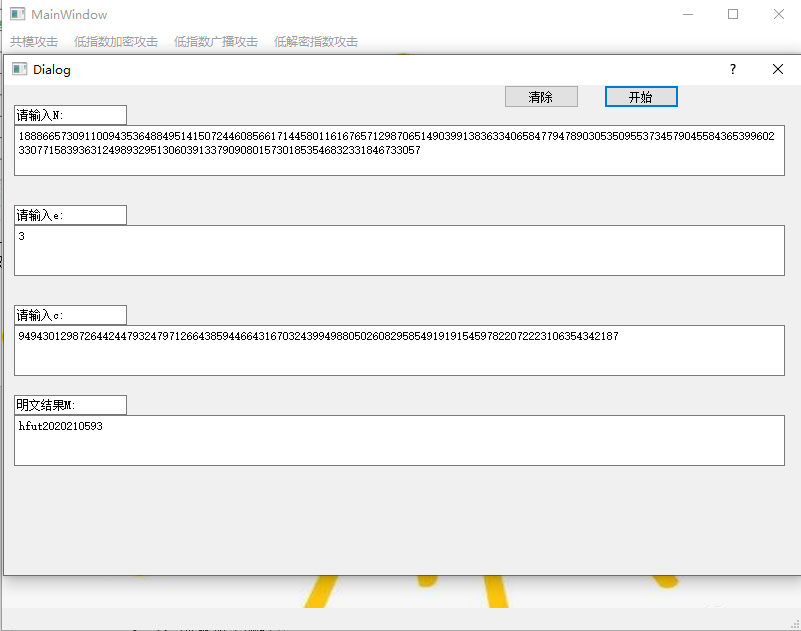
图 20 低加密指数攻击测试1

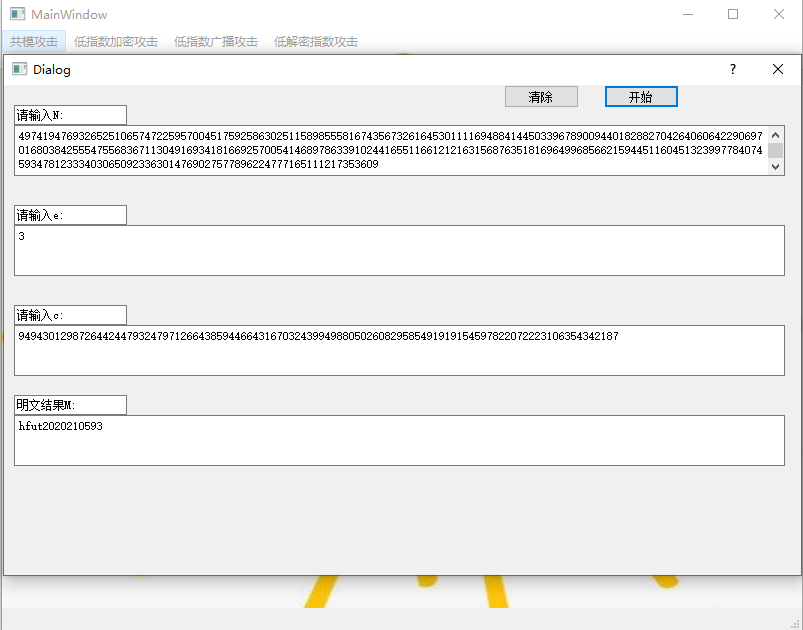
图 21 低加密指数攻击测试2

3、低加密广播攻击测试

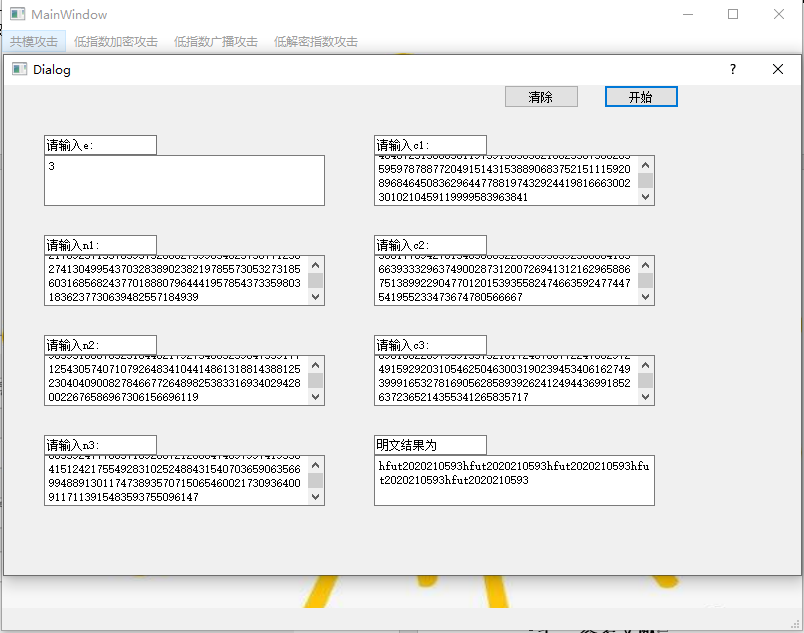
图 22 低加密广播攻击测试1

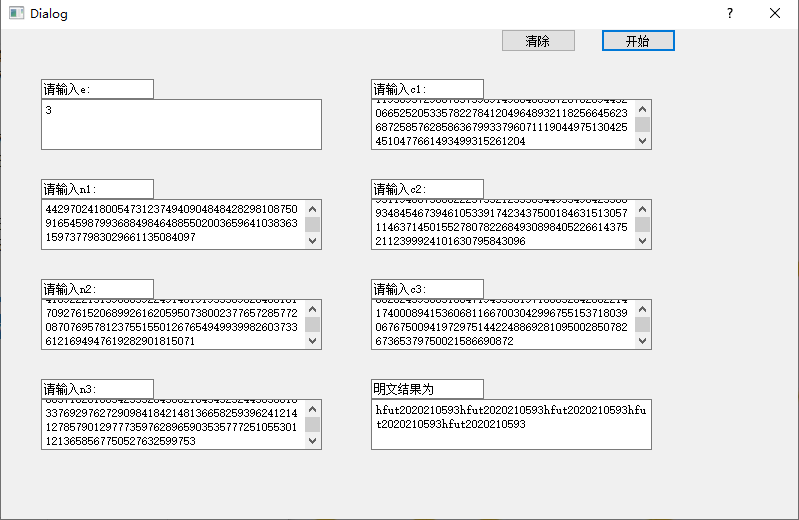
图 23 低加密广播攻击测试2

4、低解密指数攻击测试

图 24 低解密指数攻击测试1

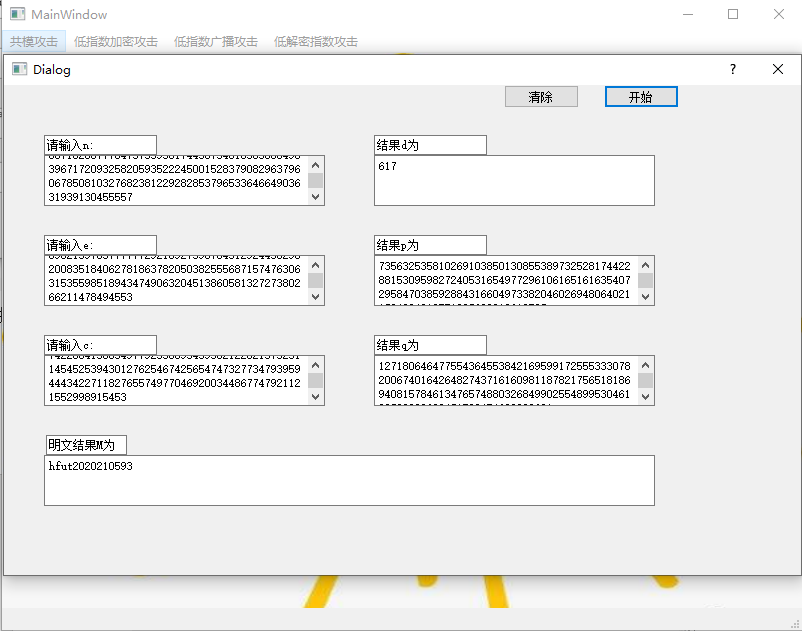
图 25 低解密指数攻击测试2

5、Dp泄露攻击测试

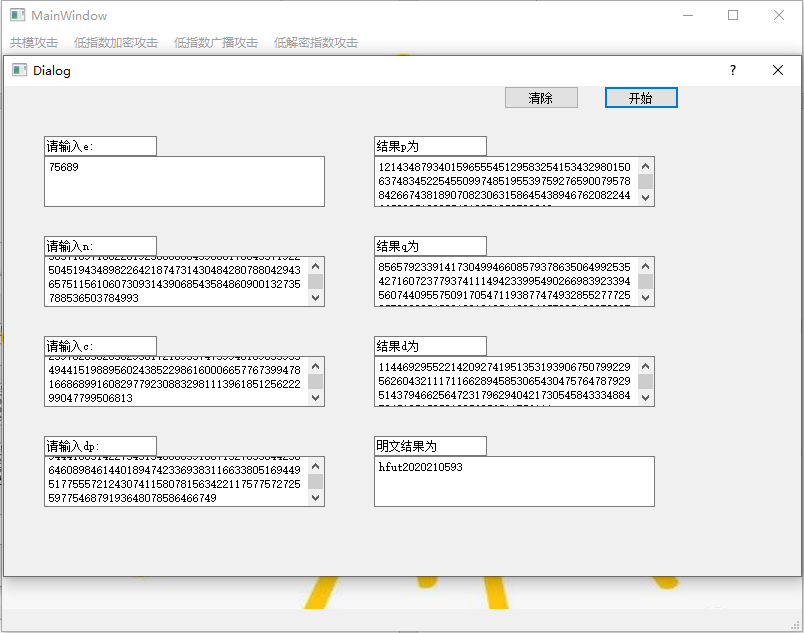
图 26 Dp泄露攻击测试1

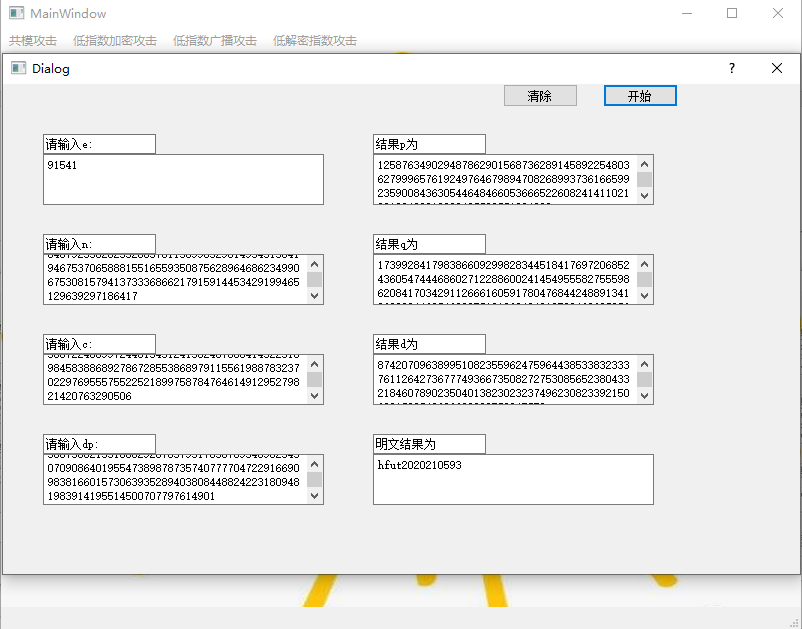
图 27 Dp泄露攻击测试2

五、安全性分析

RSA的安全性依赖于大整数的因式分解问题。实际上，人们推测RSA的安全性依赖于大整数的因式分解问题，但谁也没有在数学上证明从c和e计算m需要对n进行因式分解。可以想象可能会有完全不同的方式去分析RSA。然而，如果这种方法能让密码解析员推导出d，则它也可以用作大整数因式分解的新方法。最难以令人置信的是，有些RSA变体已经被证明与因式分解同样困难。甚至从RSA加密的密文中恢复出某些特定的位也与解密整个消息同样困难。另外，对RSA的具体实现存在一些针对协议而不是针对基本算法的攻击方法。

六、总结展望

1、经过对RSA安全性的分析，可以得出使用RSA时应该注意的事项：
•随机选择足够大素数（目前应在512位以上）；
•在使用RSA的通信网络协议中，不应该使用公共模（使用者知道f(n)）；
•不要让攻击者得到原始的解密结果；
•解密密钥d相对模数n来说不应过小；
•应该或者加密密钥大；或者被加密的信息m总是大而且m不能是一些已知值的乘积，后面一种情况可以在加密前对m填充随机值实现。
•相关的消息不能用同样的密钥加密，加密前对消息进行随机值填充破坏消息之间的代数联系及相关性，但是要注意填充算法的选择；
•应该使获得对任意值的原始签名不可能。
•被签名的消息应该与模数差不多大，而且不是一些已知值的乘积；
•使用平均解密时间和混乱(blinding)等方法使时间攻击中使用的统计手段失效；
•如果有条件，采用规模差别比较大的质因子p,q来提高系统的安全性；
2、 RSA系统的参数选择
RSA系统是第一个将安全性植基于因子分解的系统。很明显地，在公开密钥（e, n）中，若N能被因子分解，则在模N中所有元素价的最小公倍数（即所谓陷门）φ(N)=(p-1)(q-1)即无从隐藏。使得解密密钥d不再是秘密，进而整个RSA系统即不安全。虽然迄今人们尚无法“证明”，破解RSA系统等于因子分解。但一般“相信”RSA系统的安全性，等价于因子分解。即：若能分解因子N，即攻破RSA系统；
若能攻破RSA系统，即分解因子N（相信，但未证明）因此，在使用RSA系统时，对于公开密钥N的选择非常重要。必须使得公开N后，任何人无法从N得到T。此外，对于公开密钥e与解密密钥d，亦需有所限制。否则在使用上可能会导致RSA系统被攻破，或应用在密码协议上不安全。
经过分析，我们知道RSA系统安全性与系统的参数有很大关系，X.931标准对此提出以下几点：
•如果公钥e是奇数，e应与p-1，q-1互质；
•如果公钥e是偶数，e必须与(p-1)/2,(q-1)/2互质，且pq mod 8不成立；
•模数的长应该为1024+256x，x=0,1• • • • • • ；
•质数p，q应通过质数检测，使出错的概率小于 ；
•p-1,q-1,p+1,q+1应有大质数因子；
•gcd(p-1,q-1)应该小；
•p/q不应靠近两个小整数比值，且|p-q|应有大质数因子。

七、参考文献

[1] 杨波, 现代密码学(第4版), 清华大学出版社, 2017
[2] 陈恭亮. 简明信息安全数学基础. 高等教育出版社，2011
[3] Douglas R.Stinson. 密码学原理与实践. 电子工业出版社, 2009
[4] 密码学概论（朱晓玲）中国大学MOOC.合肥工业大学，2022

写在后面

想要源码的可以后台私我，只限hfut学生。