目录
题目来源
题目描述
示例
提示
题目解析
算法源码
题目来源
42. 接雨水 - 力扣(LeetCode)
题目描述
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例1
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例2
输入:height = [4,2,0,3,2,5]
输出:9
提示
- n == height.length
- 1 <= n <= 2 * 10^4
- 0 <= height[i] <= 10^5
题目解析
本题要计算所有柱子的储水量之和,而这个和其实可以分解求解每一个柱子的储水量。
而一个柱子要想储存住水,则必然在其左边有一根高柱,在其右边也有一根高柱,因为这样才能形成“凹”,才能在中间的低柱子上存储住水。
并且,中间低柱子的储水量取决于,其左边“最高的”柱子,和其右边“最高的”柱子的较矮者,比如下图中:
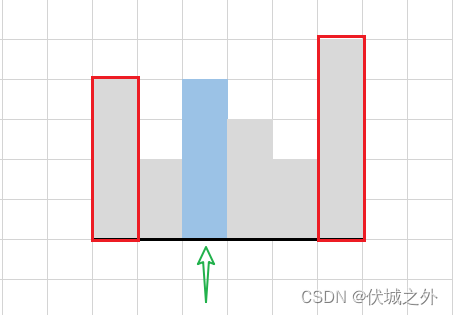
绿色箭头指向的低柱子的储水量取决于:其左边最高柱子,和其右边最高柱子的较矮者。
因此,本题其实是要我们求解每一根柱子的:
- 左边最高柱子高度
- 右边最高柱子高度
这个求解,可以使用动态规划来做:
我们假设第 i 根柱子的高度为 h[i],第 i 根柱子的左边最高柱子高度表示为left[ i ]
则第 i 根柱子的左边的最高柱子高度为:
left[ i ] = max( left[ i - 1 ], h[ i - 1 ] )
什么含义呢?
第 i 根柱子左边的最高柱子:
- 要么是 第 i - 1 根柱子,即h[ i - 1 ]
- 要么是 第 i - 1 根柱子的左边的最高柱子,即 left[ i - 1 ]
我们只要从左到右完成left数组的初始化即可。
同理,可得:
right[ i ] = max( right[ i + 1 ], h[ i + 1 ] )
此时需要从右往左完成right数组的初始化。
这样的话,第 i 根柱子的储水量
取决于其左边最高柱子,和其右边最高柱子的较矮者,即min(left[ i ], right[ i ])
第 i 根柱子的储水量val = min(left[ i ], right[ i ]) - h[ i ]
注意val最小为0,不能为负数。因此最终第 i 根柱子的储水量计算公式为:
max(0, min(left[ i ], right[ i ]) - h[i])
我们只要累加每根柱子的储水量即为题解。
Java算法源码
class Solution {
public int trap(int[] h) {
int n = h.length;
// left[i] 表示 第 i 根柱子的左边的最高的柱子的高度
int[] left = new int[n];
for(int i=1; i<n; i++) {
// 第 i 根柱子左边最高的柱子要么是h[i-1],即第i-1根柱子的高度,要么是left[i-1],即第i-1根柱子的左边的最高的柱子的高度
left[i] = Math.max(left[i-1], h[i-1]);
}
// right[i] 表示 第 i 根柱子的右边的最高的柱子的高度
int[] right = new int[n];
for(int i=n-2; i>=0; i--) {
// 第 i 根柱子右边最高的柱子要么是h[i+1],即第i+1根柱子的高度,要么是right[i+1],即第i+1根柱子的右边的最高的柱子的高度
right[i] = Math.max(right[i+1], h[i+1]);
}
int ans = 0;
for(int i=1; i<n-1; i++) {
// 第i根柱子最多能蓄水的量,取决于其左边最高的柱子和右边最高的柱子的较矮的那个,且较矮的那根柱子 - 第i根柱子的高度就是第i根柱子的蓄水量,注意蓄水量最少为0
ans += Math.max(0, Math.min(left[i], right[i]) - h[i]);
}
return ans;
}
}
JS算法源码
/**
* @param {number[]} height
* @return {number}
*/
var trap = function(h) {
const n = h.length
// left[i] 表示 第 i 根柱子的左边的最高的柱子的高度
const left = new Array(n).fill(0)
for(let i=1; i<n; i++) {
// 第 i 根柱子左边最高的柱子要么是h[i-1],即第i-1根柱子的高度,要么是left[i-1],即第i-1根柱子的左边的最高的柱子的高度
left[i] = Math.max(left[i-1], h[i-1])
}
// right[i] 表示 第 i 根柱子的右边的最高的柱子的高度
const right = new Array(n).fill(0)
for(let i=n-2; i>=0; i--) {
// 第 i 根柱子右边最高的柱子要么是h[i+1],即第i+1根柱子的高度,要么是right[i+1],即第i+1根柱子的右边的最高的柱子的高度
right[i] = Math.max(right[i+1], h[i+1])
}
let ans = 0
for(let i=1; i<n-1; i++) {
// 第i根柱子最多能蓄水的量,取决于其左边最高的柱子和右边最高的柱子的较矮的那个,且较矮的那根柱子 - 第i根柱子的高度就是第i根柱子的蓄水量,注意蓄水量最少为0
ans += Math.max(0, Math.min(left[i], right[i]) - h[i])
}
return ans
};
Python算法源码
class Solution(object):
def trap(self, h):
"""
:type height: List[int]
:rtype: int
"""
n = len(h)
# left[i] 表示 第 i 根柱子的左边的最高的柱子的高度
left = [0]*n
for i in range(1, n):
# 第 i 根柱子左边最高的柱子要么是h[i-1],即第i-1根柱子的高度,要么是left[i-1],即第i-1根柱子的左边的最高的柱子的高度
left[i] = max(left[i-1], h[i-1])
# right[i] 表示 第 i 根柱子的右边的最高的柱子的高度
right = [0]*n
for i in range(n-2,0,-1):
# 第 i 根柱子右边最高的柱子要么是h[i+1],即第i+1根柱子的高度,要么是right[i+1],即第i+1根柱子的右边的最高的柱子的高度
right[i] = max(right[i+1], h[i+1])
ans = 0
for i in range(1, n-1):
# 第i根柱子最多能蓄水的量,取决于其左边最高的柱子和右边最高的柱子的较矮的那个,且较矮的那根柱子 - 第i根柱子的高度就是第i根柱子的蓄水量,注意蓄水量最少为0
ans += max(0, min(left[i], right[i]) - h[i])
return ans