核心思想
本文提出一种基于图对抗神经网络的图匹配算法(GAMnet),使用图神经网络作为生成器分别生成源图和目标图的节点的特征,并用一个多层感知机作为辨别器来区分两个特征是否来自同一个图,通过对抗训练的办法提高生成器特征提取的质量。然后采用可学习的方式获取节点关联矩阵和边关联矩阵。最后,设计了一个稀疏的图匹配求解器,相对于连续空间内的求解方法,该方法引入了图匹配中节点一一匹配的稀疏约束。并且这个操作是可微的,因此整个网络可以端到端的训练。
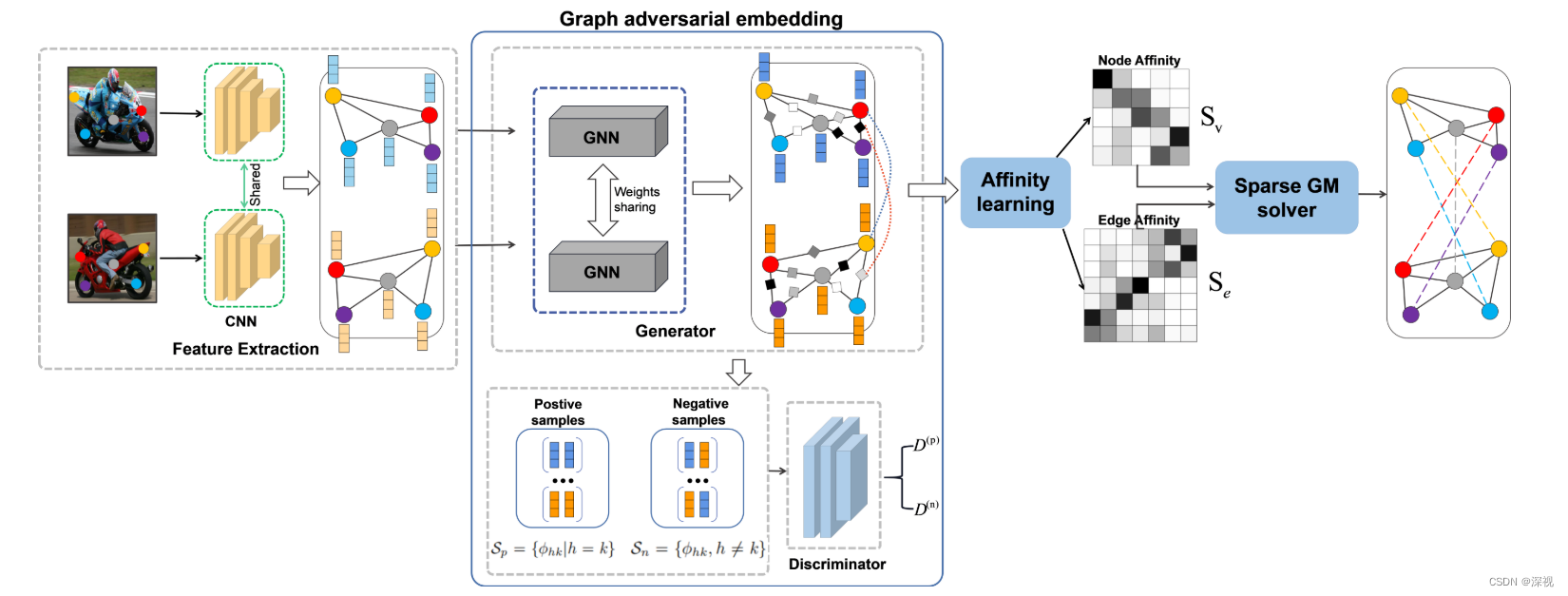
实现过程
首先,给出图的定义形式,本文采用的是节点-边指示矩阵的表示方法
G
=
{
X
,
Z
,
G
,
H
}
G=\{\mathbf{X,Z,G,H}\}
G={X,Z,G,H},其中
X
\mathbf{X}
X表示节点特征,
Z
\mathbf{Z}
Z表示边特征,
G
,
H
\mathbf{G,H}
G,H表示节点-边指示矩阵,用于描述节点之间的连接关系。对于源图
G
s
G_s
Gs和目标图
G
t
G_t
Gt分别包含
n
s
n_s
ns和
n
t
n_t
nt个节点,节点和边的关联矩阵分别为
S
v
\mathbf{S_v}
Sv和
S
e
\mathbf{S_e}
Se,图匹配的目标就是寻找最优的节点对应关系(匹配)矩阵
P
∈
{
0
,
1
}
n
s
×
n
t
\mathbf{P}\in\{0, 1\}^{n_s\times n_t}
P∈{0,1}ns×nt,目标函数与约束条件如下
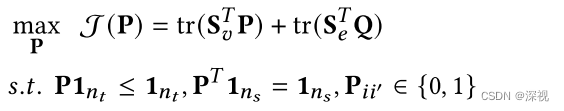
其中
Q
=
(
H
s
T
P
H
t
⊙
G
s
T
P
G
t
)
\mathbf{Q=(H_s^TPH_t\odot G_s^TPG_t)}
Q=(HsTPHt⊙GsTPGt),
Q
\mathbf{Q}
Q中的每个元素描述了两幅图边和边之间的匹配关系。
给定源图
G
s
G_s
Gs和目标图
G
t
G_t
Gt,利用图神经网络作为生成器
G
\mathcal{G}
G用于提取对应的特征
X
~
s
\widetilde{\mathbf{X}}_s
X
s和
X
~
t
\widetilde{\mathbf{X}}_t
X
t
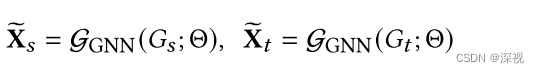
Θ
\Theta
Θ表示网络参数,本文选用SplineCNN作为生成器。经过特征提取得到源图和目标图中每个节点的特征向量
x
~
h
∈
X
~
h
\widetilde{x}_h\in\widetilde{\mathbf{X}}_h
x
h∈X
h和
x
~
k
∈
X
~
k
\widetilde{x}_k\in\widetilde{\mathbf{X}}_k
x
k∈X
k,其中
h
,
k
∈
{
s
,
t
}
h,k\in\{s,t\}
h,k∈{s,t},这表示
x
~
h
\widetilde{x}_h
x
h和
x
~
k
\widetilde{x}_k
x
k既有可能来自与源图也有可能来自于目标图,作者将二者组合成一个节点对
ϕ
h
k
=
(
x
~
h
,
x
~
k
)
\phi_{hk}=(\widetilde{x}_h,\widetilde{x}_k)
ϕhk=(x
h,x
k),如果
h
=
k
h=k
h=k则两者来自同一个图,如果
h
≠
k
h\neq k
h=k则两者来自不同的图。根据两者是否来自同一个图,可以将所有的节点对分成正节点对
S
p
\mathcal{S}_p
Sp和负节点对
S
n
\mathcal{S}_n
Sn两类
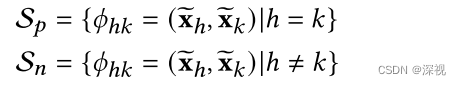
通过特征向量逐元素相加的
x
~
h
+
x
~
k
\widetilde{x}_h+\widetilde{x}_k
x
h+x
k方式得到节点对
ϕ
h
k
\phi_{hk}
ϕhk的特征向量,并利用一个由多层感知机构成的辨别器来区分当前输入的节点对是否来自同一个图,辨别器输出一个类别指示向量
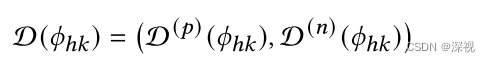
D
(
p
)
(
ϕ
h
k
)
\mathcal{D}^{(p)}(\phi_{hk})
D(p)(ϕhk)表示该节点对为正节点对的概率,
D
(
n
)
(
ϕ
h
k
)
\mathcal{D}^{(n)}(\phi_{hk})
D(n)(ϕhk)表示该节点对为负节点对的概率。在生成器和辨别器对抗训练的过程中,生成器要不断提高源图和目标图匹配节点特征的相似性,以混淆辨别器。辨别器也要不断提高区分能力,以分辨两个节点特征是否来自同一个图。图对抗神经网络的损失函数为
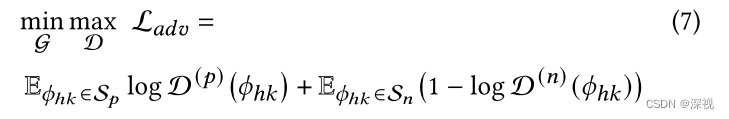
得到节点的特征向量
x
~
s
,
x
~
t
\widetilde{x}_s,\widetilde{x}_t
x
s,x
t后,边特征向量
z
~
s
,
z
~
t
\widetilde{z}_s,\widetilde{z}_t
z
s,z
t是对应两个节点的特征向量之差。然后可以构建节点关联矩阵
S
v
\mathbf{S_v}
Sv和边关联矩阵
S
e
\mathbf{S_e}
Se
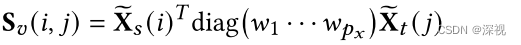
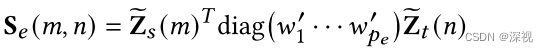
w
,
w
′
\mathbf{w,w'}
w,w′分别表示节点关联矩阵和边关联矩阵中的可学习权重参数。
最后,作者提出一个稀疏的图匹配求解器用于计算最优匹配关系矩阵
P
\mathbf{P}
P,由于原目标函数求解是NP-hard的,因此必须要对约束条件进行一定的松弛,本文采用的是单位正交非负松弛条件,即
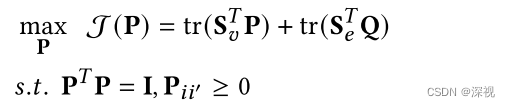
并采用一种高效的乘法更新算法(effective multiplicative update algorithm)求解上述目标函数。具体而言,给定一个初始化的解
P
(
0
)
\mathbf{P}^{(0)}
P(0),按照下述迭代过程不断更新直至收敛
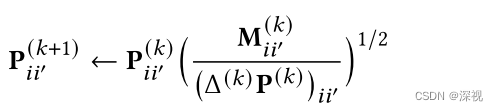
其中
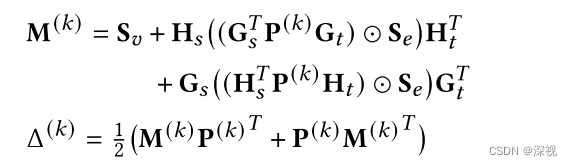
上述迭代过程最终会收敛到一个最优的稀疏解,这也就引入了离散的节点一一匹配的约束。此外,上述更新过程是连续且可微的,因此可以采用端到端的训练方法。为了保证得到的最有对应关系矩阵
P
\mathbf{P}
P与真实的匹配矩阵
H
\mathbf{H}
H保持尺度一致性,作者进一步采用了Sinkhorn算法作为一种规范化处理操作,这并不会改变矩阵
P
\mathbf{P}
P的稀疏性。最后作者用交叉熵损失函数对整个网络进行训练
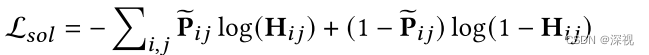
P
~
i
j
\widetilde{\mathbf{P}}_{ij}
P
ij表示对
P
\mathbf{P}
P进行Sinkhorn规范化操作。
创新点
- 采用图对抗神经网络用于特征提取
- 提出了一种稀疏的图匹配求解器,引入了节点一一匹配的约束
算法总结
本文是我看到的首次将图对抗神经网络应用到图匹配领域中的,利用对抗训练的方式增加匹配点之间的特征相似度,而增大非匹配点之间的差异性,提高匹配的效果。但本文是减少了不同图之间特征的差异性,来试图混淆辨别且。这会不会导致,两个来自不同的图的非匹配点之间的差异性也变小呢?这一点我还没有搞清楚。