1.堆排序

堆排序即利用堆的思想来进行排序，总共分为两个步骤：
1.建堆
升序：大堆
降序：小堆
2.利用堆删除思想来排序

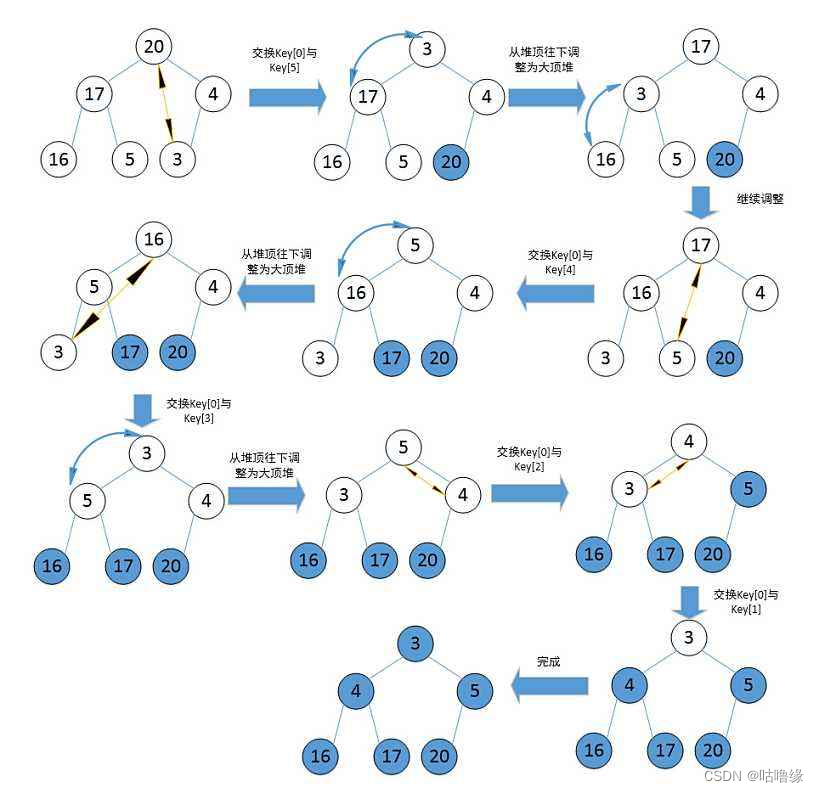
1.1代码实现

void Heapsort(int* a, int n)
{
	for (int i = (n - 1 - 1) / 2; i >= 0; --i)//建大堆
	{
		AdjustDown(a, n, i);
	}
	int end = n - 1;
	while (end > 0)
	{
		Swap(&a[0], &a[end]);
		AdjustDown(a, end, 0);
		end--;
	}
}

2. TOP-K问题

2.1原理

TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。
比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
对于Top-K问题，能想到的最简单直接的方式就是排序，但是：如果数据量非常大，排序就不太可取了(可能数据都不能一下子全部加载到内存中)。最佳的方式就是用堆来解决，基本思路如下

1. 用数据集合中前K个元素来建堆
   前k个最大的元素，则建小堆前k个最小的元素，则建大堆
   为什么求最大的k个建小堆，最小的k个建大堆？

如果求最大的k个建大堆的话，这里假设k=5，我们建了大堆以后，假如第6个元素就是最大的那个，当他进堆以后，第二大第三大的都进不来了，所以我们要建小堆

2. 用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素
   将剩余N-K个元素依次与堆顶元素比完之后，堆中剩余的K个元素就是所求的前K个最小或者最大的元素。

2.2实例分析

这道题假设求最小的五个，也就是k=5

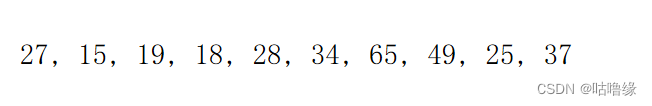
先给定一组数据

对前k个建堆（建大堆求最小的k个）

for (int i = (k - 1 - 1) / 2; i >= 0; --i)
	{
		AdjustDown(a, k, i);
	}

用堆顶元素与剩下的元素比较，小的进堆，并向下排序

int j = 0;
	for (j = k; j < n; j++)
	{
		if (a[j] < a[0])
		{
			a[0] = a[j];
			AdjustDown(a, k, 0);
		}
	}