参考:《漫画算法-小灰的算法之旅》
目录
参考:《漫画算法-小灰的算法之旅》
1、什么是归并排序
2、归并的具体操作
3、代码
4、时间复杂度和空间复杂度
5、归并排序是稳定排序
1、什么是归并排序
归并排序就像是组织一场元素之间的“比武大会”,这场比武大会 分成两个阶段:
(1)分组
假设集合一共有n个元素,算法将会对集合进行逐层的对半分组。
第1层分成2个大组,每组n/2个元素;
第2层分成4个小组,每组n/4个元素;
第3层分成8个更小的组,每组n/8个元素;
……
一直到每组只有一个元素。
(2)归并
归并排序需要确定每一个元素的排列位置。当每个小组内部比较出先后顺序以后,小组之间会展开进一 步的比较和排序,合并成一个大组;大组之间继续比较和排序,再合并成更大的组.......最终,所有元素合并成了一个有序的集合。如下图所示:

2、归并的具体操作
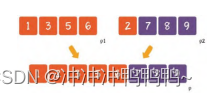
归并操作一般需要三个步骤,我们以两个长度为4的集合为例:

第1步:创建一个额外的大集合,用于存储归并结果,长度是两个小集合之和。(p1,p2,p是三个辅助指针,用于记录当前操作的位 置。)
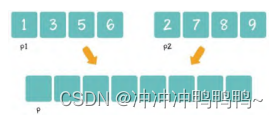
第2步:从左到右逐一比较两个小集合中的元素,把较小的元素优 先放入大集合。

第3步:从另一个还有剩余元素的集合中,把剩余元素按顺序复制 到大集合尾部。
3、代码


4、时间复杂度和空间复杂度
归并排序把集合一层一层进行折半分组。如果集合长度是n,那么 折半的层数就是logn,每一层进行归并操作的运算量是n。所以,归并排序的时间复杂度等于每一层的运算量×层级数,即 O(nlogn)。每次归并所创建的额外集合都会随着方法的结束而释放, 因此这部分空间不应该累加计算。由于单次归并操作开辟的最大空间 是n,所以归并排序的空间复杂度是O(n)。






![[Openwrt]procd实现hotplug机制介绍](https://img-blog.csdnimg.cn/img_convert/2bf4f636d1c52333ea30e498301762e9.png)