Easy Deep Learning——PyTorch中的自动微分

news2024/11/16 18:57:18

什么是深度学习？它的实现原理是怎么样的呢？

什么是梯度下降？梯度下降是怎么计算出最优解的？

什么是导数？求导对于深度学习来说有何意义？

PyTorch 自动微分（自动求导）

为什么选择这一章作为第一章而不是介绍深度学习的核心数据结构张量呢？原因在于张量运算实际就是矩阵的运算，另外PyTorch关于张量的数据处理函数很多，没必要逐个介绍，用到的时候去查文档即可，介绍过多张量的计算方式其实并无意义。

在入门深度学习时，我相信初学者最关心的是什么是深度学习？它的基本原理是怎么样的，而不是上来就列一大堆代数式，然后去进行各种数据计算。现在，读者只需要知道“张量”是PyTorch中最基本的数据结构，它是一个数组，如果要说的再清楚些，可以这样描述

在 PyTorch 中，张量（Tensor）是最基本的数据结构，是实现各种模型和算法的基础，类似于 NumPy 中的数组。它可以用来表示数字、向量、矩阵、张量等各种数据形式，同时支持 GPU 计算加速。

张量可以有不同的维度，分别是标量（0 维）、向量（1 维）、矩阵（2 维）和高维张量（3 维或更多维）。除了维度外，每个张量还有一个数据类型（如 float、int、bool 等）和一个设备类型（CPU 或 GPU）。

那么现在回到我们最关心的话题

什么是深度学习？它的实现原理是怎么样的呢？

深度学习的原理是让计算机学会从数据中提取特征，并用这些特征来解决问题。与传统的计算机程序不同，深度学习模型不需要人为地设计特征提取方式，而是让计算机自动学习。这个过程类似于人类学习语言或者乐器，我们不需要事先学会所有的单词或者音符，而是从语境或者旋律中提取出有用的信息，慢慢地积累经验并改进自己。

具体来说，深度学习模型是由神经网络组成的，每个神经元负责接收一些输入并产生一些输出。这些输入和输出可以被看做是特征的不同表示方式，例如对于图像数据，可以把像素值作为输入，然后每个神经元输出的是对应的图像特征。为了让神经网络自动学习到有用的特征，我们需要为它提供大量的数据，并让它通过反向传播算法不断调整自己的参数。

反向传播算法的基本思路是利用导数信息，从输出端反向推导神经网络中每个参数的贡献度，并根据这个贡献度来调整参数，从而让模型的预测结果更加准确。这个过程类似于一个小孩子学习画画，一开始可能会画得很丑，但是每次被告知错误的地方，就能不断改进，最终画出漂亮的图画。

总的来说，深度学习的原理是通过神经网络自动学习数据中的特征，利用反向传播算法来不断优化模型参数，从而使模型的预测结果更加准确。

说的再通俗点，可以这样描述：

深度学习就是从数据中提取特征，找到特征的规律，来得出结果。这个规律是一个函数，数据是函数的自变量，而结果就是函数的因变量。其中的规律则是函数的权重和偏置，深度学习就是通过大量的数据来求得函数的权重从而得到正确结果的。而一般数据非常复杂影响结果的自变量很多，于是这些函数组成了一个非常复杂的函数组（神经网络）。举个简单的例子

假设一个机器要学习的函数是： y = kx + b

此时只需要两组数据，例如（1，5）（ 2，7），即可求得k，b

于是求得函数表达式为 y = 2x+3 ，这个计算 k，b的过程称为 “学习”。

此时输入一个陌生的自变量，比如 3，此时机器通过两组数据进行“学习”之后，得到了函数的表达式，因此，机器将 3 代入表达式就可以得出正确结果为 9

然而如此简单的函数模型是无法匹配现实中非常复杂的问题的，那么对于非常复杂的函数，机器是怎么计算其中的 k 和 b的呢？

上面已经介绍了反向传播方法，就是从结果的好坏去纠正模型的参数，反向来优化得出结果。

下面介绍深度学习的算法基石：梯度下降算法

什么是梯度下降，梯度下降是怎么计算出最优解的？

假设你在爬山，想要到达山顶。你的目标是走到山顶，但是你并不知道应该往哪个方向走才能最快到达山顶。你的手头有一张地图，上面有你所在的位置和山的形状。

这时候，你可以利用梯度的信息来找到最快到达山顶的方向。梯度是指函数变化最快的方向，你可以把它想象成地图上高度变化最快的地方，就像一个“斜坡”的方向。

通过不断地朝着梯度的方向走，你就可以越来越接近山顶。每次走的步子大小可以通过学习率来控制，学习率越大，走的步子就越大，但是可能会“越过”山顶而错过最优解；学习率越小，走的步子就越小，但是需要更多的步数才能到达最优解。

在深度学习中，我们的目标是最小化损失函数，找到最优解。梯度下降就是一种常用的优化算法，通过不断地计算损失函数关于参数的梯度，朝着梯度的方向调整参数，使得损失函数不断减小，最终找到最优解。

接下来可能读者又会产生一个问题：计算机是怎么找到山谷高度变化最快的方向，然后沿着这个方向找答案的呢？

答案是导数。我们都知道导数表示函数在某一点上的变化率，因此导数就可以帮助我们找到函数的

最快的方向，

什么是导数？求导对于深度学习来说有何意义？

导数是微积分中的概念，表示函数在某一点上的变化率或斜率。在机器学习和深度学习中，导数（或者更一般地说，梯度（可以理解为山谷的斜坡高度））具有至关重要的作用。

首先，导数可以帮助我们找到函数的极值点（最大值或最小值）。在深度学习中，我们通常会用损失函数（每上一个台阶，距离山顶高度最优的直线距离的偏差，就是你要多走的路，在函数中定义为损失）来衡量模型的预测与真实值之间的误差，我们的目标就是最小化这个损失函数。通过计算损失函数关于模型参数的导数，我们可以找到使得损失函数最小化的参数值，从而优化模型。

其次，导数可以帮助我们理解函数的变化规律，例如函数的单调性和凸凹性。在深度学习中，我们通常会通过观察损失函数随着模型参数的变化趋势来判断模型的训练情况和性能。

如此复杂的函数模型，如果让我们手动求导显然工作量太大了。那么有了上面的理解，引入本节知识点——自动微分。

最后，自动微分（或者说自动求导）是深度学习中非常重要的技术之一，可以帮助我们自动地计算复杂模型中的导数，从而方便模型的优化。

PyTorch深度学习框架都提供了自动微分功能，可以大大简化模型开发过程中的计算难度和计算量。

PyTorch自动微分（自动求导）

PyTorch中的自动微分（自动求导）主要通过torch.autograd模块来实现。其中，最常用的函数是torch.Tensor.backward()，它可以自动计算张量的梯度（梯度就是导数值），并将结果存储在grad属性中。在计算张量的导数之前，需要设置该张量可导，requires_grad=True

举一个简单的例子，假设我们有一个函数y = 2x^2 + 3x + 1，可以通过以下代码实现它的自动微分：
import torch

x = torch.tensor(2.0, requires_grad=True) # 定义张量x，并开启梯度追踪
y = 2 * x**2 + 3 * x + 1

y.backward() # 自动计算y对x的梯度

print(x.grad) # 输出梯度
输出的结果为11。我们手动验证下：

y = 2x^2 + 3x + 1 的导数为 y = 4x +3，x=2 代入得：

y = 4 * 2 + 3 = 11

验证正确。

下面再举一个例子

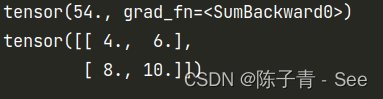
import torch

x = torch.tensor([[1.0,2.0],[3.0,4.0]],requires_grad = True)

y = torch.sum(x**2+2*x+1)
#sum函数：将x的每一个值带入表达式的值,然后求和
print(y) # 54 = 4 + 9 + 16 + 25
y.backward() # 求解y关于x的导数
print(x.grad)