目录
- 1.先序遍历
- 2.中序遍历
- 3.后序遍历
- 4.层序遍历(可用于需按层进行计算的题目)
- 5.判定二叉树的对称性
- 6.二叉树最大深度(结点深度:根节点到该结点。结点高度:该结点到叶子结点)
- 7.二叉树最小深度
- 8.二叉树的平衡性
- 9.求左叶子的和
- 10.通过中序和后序序列构造二叉树
- 11.二叉搜索树相关问题
- 11.1.验证二叉搜索树的性质(这题我用了前序遍历)
- 11.2.二叉搜索树的最小绝对差
- 12.公共祖先问题
1.先序遍历
void PreOrder(TreeNode* root){
if(root==NULL)
return;
//要对头结点进行的操作
if(root->left!=NULL)
PreOrder(root->left);
if(root->right!=NULL)
PreOrder(root->right);
}
2.中序遍历
void InOrder(TreeNode* root){
if(root==NULL)
return;
if(root->left!=NULL)
InOrder(root->left);
//要对头结点进行的操作
if(root->right!=NULL)
InOrder(root->right);
}
3.后序遍历
void PostOrder(TreeNode* root){
if(root==NULL)
return;
if(root->left!=NULL)
PostOrder(root->left);
if(root->right!=NULL)
PostOrder(root->right);
//要对头结点进行的操作
}
4.层序遍历(可用于需按层进行计算的题目)
//直接给出函数体
if(root==NULL)
return;
queue<TreeNode*> q;//创建队列,也可以用大点的数组然后双指针
TreeNode* temp;
q.push(root);//头结点入队
int size;//用来保存当轮结点数量
while(!q.empty()){
size=q.size();//统计当层结点数量
for(int i=0;i<size;i++){//把单层结点出队完,for循环才结束
temp=q.front();
q.pop();//队头结点出队
if(temp->left!=NULL)
q.push(temp->left);//左孩子入队
if(temp->right!=NULL)
q.push(temp->right);//右孩子入队
}
}
5.判定二叉树的对称性
bool isSymmetric(TreeNode* left,TreeNode* right){
if(left==NULL&&right==NULL)//两个结点同时为空则对称
return true;
if(left==NULL||right==NULL)
//同时为空的情况被上面筛去了,这里判断的是只有一方为空,则不对称
return false;
if(left->val!=right->val)
//值不一样,不对称
return false;
bool t1=isSymmetric(left->left,right->right);
//递归判断左子树的左孩子和右子树的右孩子
bool t2=isSymmetric(left->right,right->left);
//递归判断左子树的右孩子和右子树的左孩子
return t1&&t2;//同时为真才对称
}
6.二叉树最大深度(结点深度:根节点到该结点。结点高度:该结点到叶子结点)
int getMaxDepth(TreeNode* root){
if(root==NULL)
return 0;
int left=getMaxDepth(root->left);
int right=getMaxDepth(root->right);
int depth=(left>right?left:right)+1;
return depth;
}
7.二叉树最小深度
int getMinDepth(TreeNode* root){
if(root==NULL)
return 0;//结点为空,深度为0
if(root->left==NULL&&root->right==NULL)
return 1;//叶子结点深度为1
int left=INT_MAX://左子树深度,初始化为最大值
int right=INT_MAX;//右子树深度。初始化为最大值
if(root->left!=NULL)
left=getMinDepth(root->left);
if(root->right!=NULL)
right=getMinDepth(root->right);
//只有子树非空,才返回小的深度,否则数值都是最大值MAX_INT
//控制住每层深度缩小的途径
return left>right?right:left;
//将左、右子树中较小的深度值返回
}
8.二叉树的平衡性
int isBalance(TreeNode* root){//这个函数设定返回-1说明不平衡
if(root==NUL)
return 0;
int left=0;
int right=0;
int res;
if(root->left!=NULL)//左子树非空,递归左子树
left=isBalance(root->left);
if(root->right!=NULL)//右子树非空,递归右子树
right=isBalance(root->right);
if(left==-1||right==-1)//左右子树有一个不平衡,则整棵树不是平衡树
res=1-;
else{//左右子树平衡,则判断当层
if(abs(left-right)>1)//左右子树高度差大于一,则不平衡
res=-1;
else//否则,返回左右子树中最大的深度,再加上当层的深度1
res=(left>right?left:right)+1;
}
return res;
}
9.求左叶子的和
int sumOfLeftLeaves(TreeNode *root){
if(root==NULL)
return 0;
int left;
if(root->left!=NULL&&root->left->left==NULL&&root->left->right==NULL)
left=root->left->val;
else
left=sumOfLeftLeaves(root->left);
int right=sumOfLeftLeaves(root->right);
return left+right;
}
10.通过中序和后序序列构造二叉树
TreeNode* BuildTree(vector<int>& inorder, vector<int>& postorder,int ll,int lr,int pl,int pr){
//ll、lr是中序序列的下标范围,pl、pr是后序序列的下标范围
if(pl>pr)
return NULL;
TreeNode* root=new TreeNode(postorder[pr]);
int index;
for(index=0;index<inorder.size();index++){
if(inorder[index]==root->val)
break;
}
root->left=BuildTree(inorder,postorder,ll,index-1,pl,pl+index-1-ll);
root->right=BuildTree(inorder,postorder,index+1,lr,pl+index-ll,pr-1);
return root;
}
其实可以抽象出一个用数组构造二叉树的模板
if(左下标>右下标)//先标出结束递归的条件,即出口
return NULL;
TreeNode* root=new TreeNode(结点的值);//构造本结点
root->left=(递归调用函数);//构造本结点的左子树
root->right=(递归调用函数);//构造本结点的右子树
11.二叉搜索树相关问题
由于二叉搜索树全树具有 左子树<当前结点<右子树 的特点,所以很多都要用到中序遍历(在中序遍历中,全树结点的遍历顺序为左子树结点->当前结点->右子树结点,因此遍历出来得到的序列为升序序列),利用二叉搜索树的特性进行遍历。
另外,如果遇到要保留二叉搜索树某个范围的结点的话(修剪二叉搜索树),如果根节点满足条件,而左子树某结点不满足保留条件,要删除的话,需要判断该结点的右子树是否满足条件。
因为如果左子树某结点不满足保留的范围的话,由于二叉搜索树具有的 左子树<当前结点<右子树 性质,因此该结点一定是小于保留的范围的,而该结点的右子树大于该结点,所以不能直接删除,需要继续判断右子树是否满足保留条件。
根节点的右子树同理。
11.1.验证二叉搜索树的性质(这题我用了前序遍历)
long long min_num=LONG_MIN;
long long max_num=LONG_MAX;
bool isValid(TreeNode *root,long long min_num,long long max_num){
if(root==NULL)
return true;
if(root->val<=min_num)
return false;
if(root->val>=max_num)
return false;
bool left=isValid(root->left,min_num,root->val);
//因为左子树<当前结点,所以当前结点比左子树任何结点都大
//因此把当前结点的值作为最大值传入
bool right=isValid(root->right,root->val,max_num);
//因为当前结点<右子树,所以当前结点比右子树任何结点都小
//因此把当前结点的值作为最小值传入
}
11.2.二叉搜索树的最小绝对差

这题需要计算每两个结点之间的差值,并返回其中的最小值。由于在中序遍历中序列的值呈升序,而在该升序中序列,每个数的大小肯定是跟与之相邻的数的大小最接近,因此可以采用中序遍历的方式,从前向后两两计算前后两个结点的差值,取出其中的最小值。
但是在之前的中序遍历中,我们只能看到当前结点的值,最多是当前结点的左右子树的值,如果遇到以下这种情况,如何判断1号结点和3号结点的值呢?
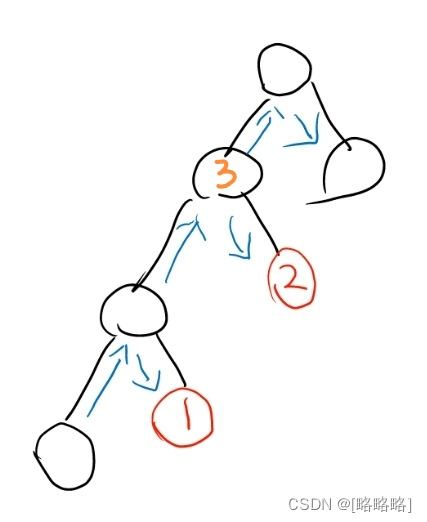
我们可以用一个结点专门保存上一个结点的指针,当轮计算完成后再用该结点保存当前结点的指针,遍历下一个结点,以下是代码,也可以作为需要比较树的前后关系的模板。
void getMin(TreeNode* root,TreeNode*& pre,int& min){
if(root==NULL)
return;
if(root->left!=NULL)
getMin(root->left,pre,min);
//以上是中序遍历模板
if(pre!=NULL){
int temp=abs(pre->val-root->val);
if(temp<min)
min=temp;
}
//以下两行是中序遍历模板
if(root->right!=NULL)
getMin(root->right,root,min);
pre=root;
//修改pre再返回,比如当前正在访问上面图片的1号结点,执行到这里后
//会将1号结点保存后再返回,然后会一路返回到2号的父节点3号
//进行if(pre!=NULL)那一行的计算,对比pre(即1号结点)和3号结点的值
//这就是 pre=root 的用意
}
12.公共祖先问题
因为后序遍历的顺序为 左子树->右子树->当前结点 ,即从下往上找,因此可以采用后序遍历寻找树的公共祖先
TreeNode* CommonAncestor(TreeNode* root,TreeNode* p,TreeNode* q){
if(root==NULL)
return NULL;
//用来保存左右子树的寻找结果,初始化为NULL
//一定要提前声明,因为if不一定满足条件,没提前声明又不满足的话,最后会报错
TreeNode* left=NULL;
TreeNODe* right=NULL;
//后序遍历
if(root->left!=NULL)
left=CommonAncestor(root->left,p,q);
if(root->right!=NULL)
right=CommonAncestor(root->right,p,q);
//如果当前结点是想寻找的其中一个结点,就返回此结点
if(root==p||root==q)
return root;
//如果左右子树都非空,说明这个root的左右子树中分别有p或q,说明root是最近的公共祖先
if(left&&right)
return root;
//如果左子树或右子树存在非空值,返回此值,否则返回的是NULL
return (left?left:right);
}