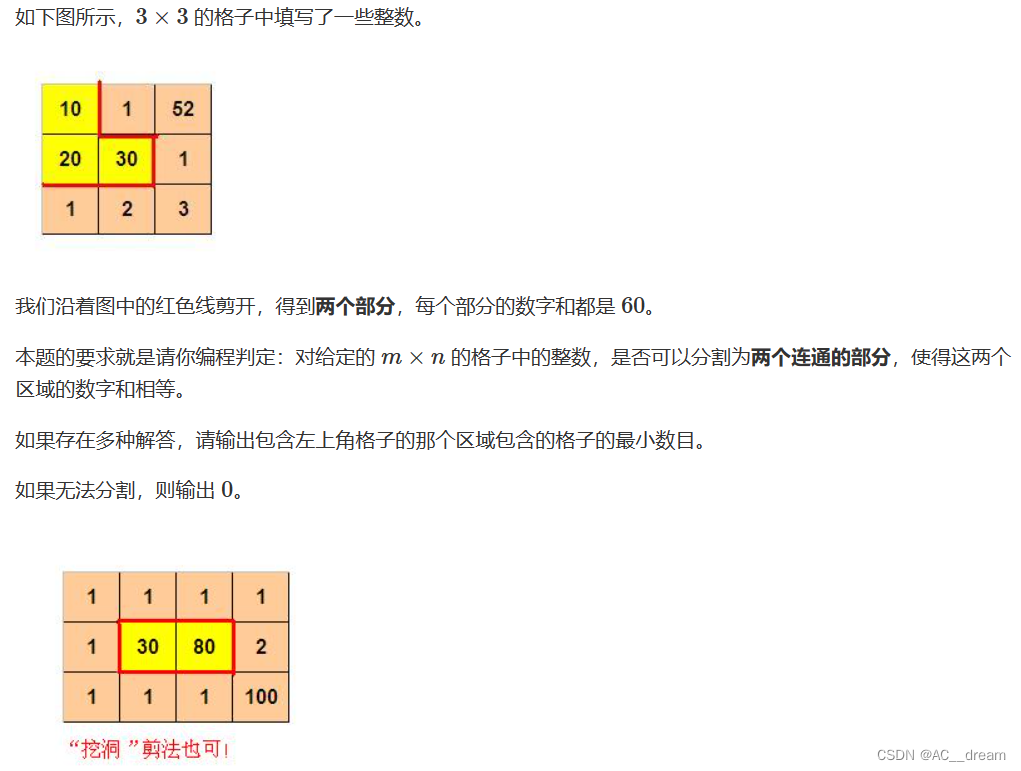

样例1输入:
3 3
10 1 52
20 30 1
1 2 3样例1输出:
3样例2输入:
4 3
1 1 1 1
1 30 80 2
1 1 1 100样例2输出:
10分析:这道题目我们直接从(1,1)点开始进行dfs搜索即可,但是需要注意一点的是我们搜索的时候并不是沿着一条路径进行搜索,而是从当前已经走过的所有点中选出一个点然后沿着不同方向去搜索,这样我们就可以搜出所有的连通块,每次搜出一个连通块时还需要检测剩余的部分是否是一个连通块,那么检测剩余部分是否是一个连通块我们可以用并查集来实现。这样大体的步骤就实现了,接下来就是剪枝了,为了防止同样的状态被多次搜索,我们可以用哈希优化一下,随意设置一个哈希函数,然后求出每个连通块对应的哈希值然后进行去重即可,还有可以优化的一点就是我们每次尽可能选取值大的点进行搜索,这样得到目标值的连通块内的点就会尽可能小。
需要说明的一点就是:由于蓝桥原题是没有明确说明两部分都必须连通的,所以也就没必要加上判断连通的那部分,而且他数据中都是一笔画形成的连通块,没有考虑周全,所以本代码在这两方面进行了优化,但会在洛谷上提交时会有一个点超时,那是因为本代码充分考虑到其余部分是否连通以及连通块形状任意这两个问题。
细节见代码:
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
#include<unordered_set>
using namespace std;
typedef pair<int,int> PII;
const int N=12;
const int P=13331;//P用于哈希
unordered_set<unsigned long long>st;
PII p[N*N];//存放当前已选的点
int a[N][N];
bool vis[N][N];
int fu[N*N],sum,ans,n,m;
int dx[4]={0,0,1,-1},dy[4]={1,-1,0,0};
bool cmp(PII x,PII y)
{
return a[x.first][x.second]>a[y.first][y.second];
}
int find(int x)
{
if(fu[x]!=x) return fu[x]=find(fu[x]);
return x;
}
bool check_connect(int cnt)//检查剩余的n*m-cnt个点是否连通
{
for(int i=1;i<=n*m;i++) fu[i]=i;
int t=n*m-cnt;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(!vis[i][j])
{
for(int k=0;k<4;k++)
{
int nx=i+dx[k],ny=j+dy[k];
if(nx<1||nx>n||ny<1||ny>m) continue;
if(vis[nx][ny]) continue;
int fx=find((i-1)*m+j),fy=find((nx-1)*m+ny);
if(fx==fy) continue;
t--;
fu[fx]=fy;
}
}
return t==1;
}
bool check_exit()//检查当前连通块是否已经被搜索过,是的话返回true,否则返回false
{
unsigned long long t=0;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(vis[i][j])
t=t*P+i*(P-3)+j*(P+102);
if(st.count(t)) return true;//哈希去重
st.insert(t);
return false;
}
void dfs(int s,int cnt)//s和cnt分别代表当前已经选出来的数的和及个数
{
if(s==sum/2)
{
if(check_connect(cnt)) ans=min(ans,cnt);//检查其他格子是否为一个连通块
return ;
}
if(s>sum/2||cnt>=ans) return ;//剪枝
PII next[N*N];//存放下一次搜索的点
int t=0;
for(int i=1;i<=cnt;i++)
{
int nowx=p[i].first,nowy=p[i].second;
for(int j=0;j<4;j++)
{
int nx=nowx+dx[j],ny=nowy+dy[j];
if(nx<1||nx>n||ny<1||ny>m) continue;
if(vis[nx][ny]) continue;
next[++t]={nx,ny};
}
}
sort(next+1,next+t+1,cmp);
for(int i=1;i<=t;i++)
{
if(next[i]==next[i-1]) continue;
p[cnt+1]=next[i];
vis[next[i].first][next[i].second]=true;
if(!check_exit())//检查当前连通块是否已经被搜索过
dfs(s+a[next[i].first][next[i].second],cnt+1);
vis[next[i].first][next[i].second]=false;
}
}
int main()
{
cin>>m>>n;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
{
scanf("%d",&a[i][j]);
sum+=a[i][j];
}
if(sum&1)
{
printf("0");
return 0;
}
ans=0x3f3f3f3f;
vis[1][1]=true;
p[1]={1,1};
dfs(a[1][1],1);
if(ans==0x3f3f3f3f) ans=0;
printf("%d",ans);
return 0;
}