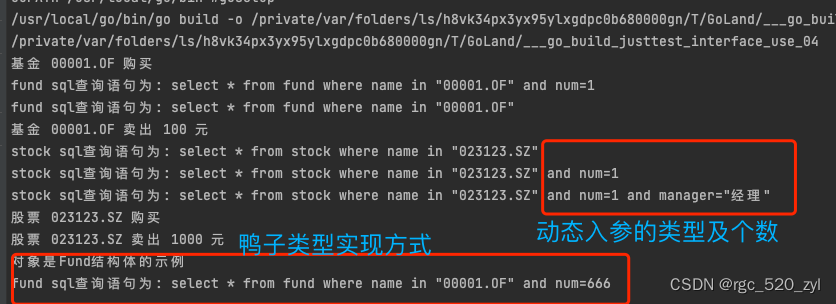
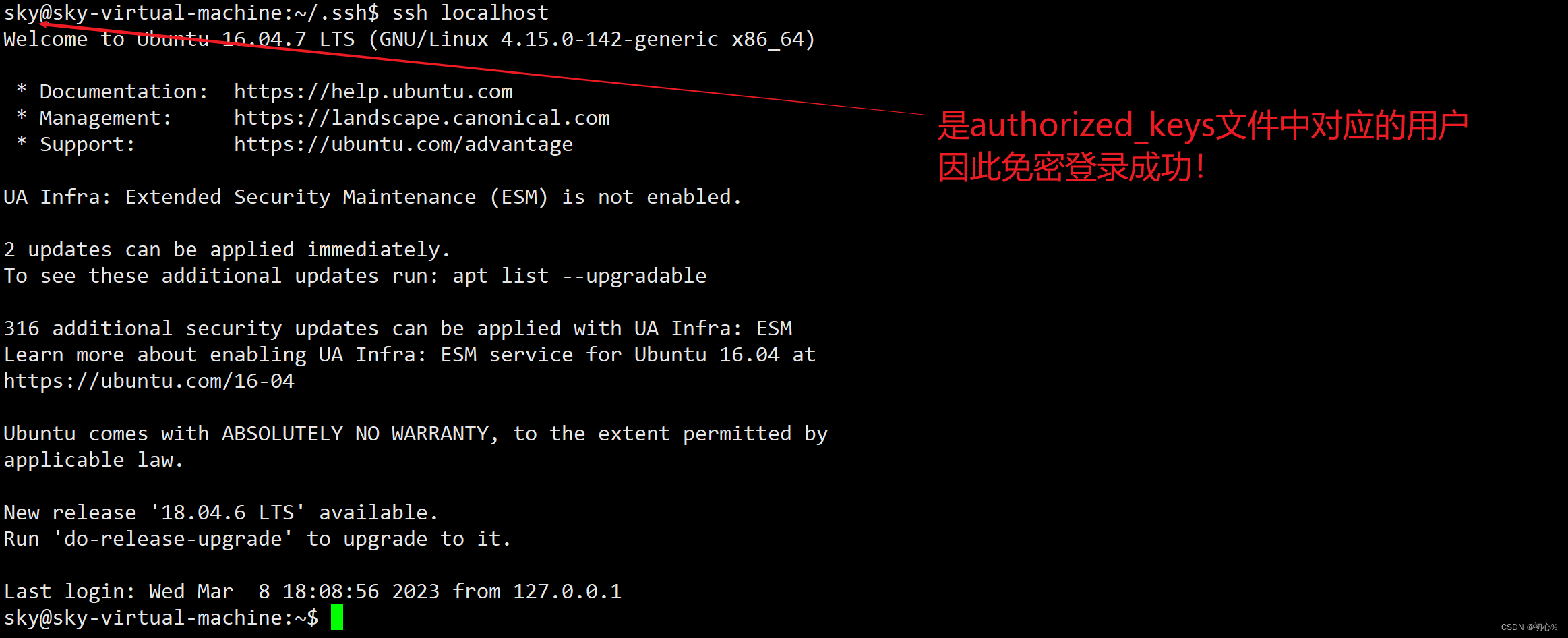
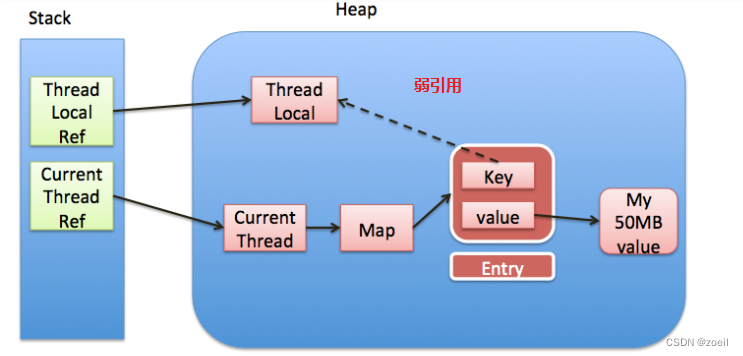
思路

算法归根到底就是找规律的游戏，我们首先来看一个现象：
以数组nums =[1,2,3,4,5]为例
当我们将数组排序后，可以知道最小值为1,最大值为5，此时我们需要四次运算可以使最小值与最大值相等：
第一次：2,3,4,5,5
第二次：3,4,5,6,5
第三次：4,5,6,7,5
第四次：5,6,7,8,5
运算次数 = 最大值 - 最小值

这时我们观察： 经过四次累加，nums = [5,6,7,8,5]，这时之前数组的最大值已经等于数组的最小值，因此我们将数组排序后会得到 nums = [5,5,6,7,8],我们重复上面的步骤，继续进行数组累加：
第一次： 6,6,7,8,8
第二次： 7,7,8,9,8
第三次： 8,8,9,10,8
运算次数 = 最大值 - 最小值

我们到这里可以总结出第一个规律：
每一轮我们使最小值等于最大值的运算次数等于数组中最大值与最小值的差值。

然后我们观察下在排序前的数组numsOld = [5,5,6,7,8] 和 numsNew = [8,8,9,10,8]可以发现虽然我们的最小值在增加的过程中向最大值趋近，但是此时次大值同样的以相同的数值进行累加成为了最新的最大值，当完成一轮加法运算后，原本的最大值就会变成最小值，次大值就会变成最大值，而我们只需要根据这个规律，就不需要重复的进行加法运算。

我们只需要从最大值开始统计每一轮使最小值与最大值相等的次数即可。
好了，让我们看代码：

    private static int minMoves(int[] nums) {
        int times = 0;
        Arrays.sort(nums);
        // 判断
        if (nums.length == 1 || nums[nums.length - 1] == nums[0]) {
            return times;
        }
        // 开启循环
        for (int i = nums.length - 1; i >= 0; i--) {
            times += nums[i] - nums[0] > 0 ? nums[i] - nums[0] : 0;
        }
        return times;
    }

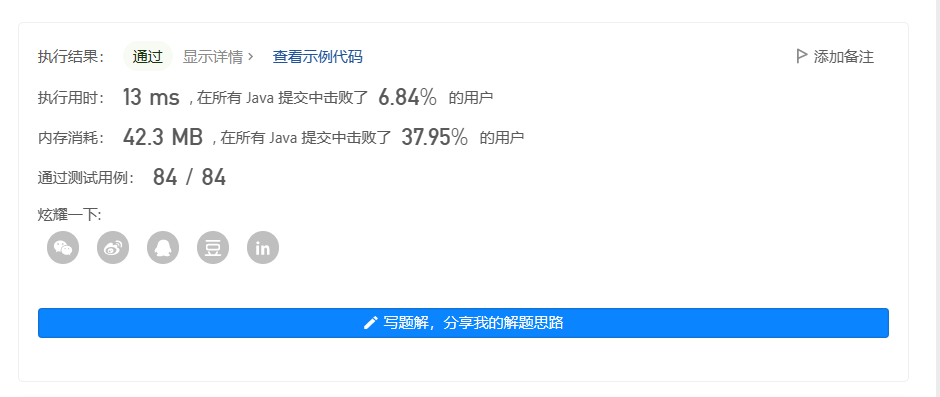
运行结果：
{:width=400}