题目描述

在这里插入图片描述

原题链接：91. 最短Hamilton路径

解题思路

动态规划五步曲：

（1）dp[i][j]含义： 到达点j并且状态为i时，具有的最短路径长度，其中状态j用状态压缩二进制的方式表示。j中从0-n-1位分别对应点0到点n-1，j中某一位的值为1时代表走入此点，值为0时代表不走入此点。

（2）递推公式： $d p [i] [j] = min (d p [i] [j], d p [i - (1 << j)] [k] + w [k] [j])$ ，其中 $d p [i - (1 << j)] [k] + w [k] [j]$ 表示在没有到达第j个点（i - (1 << j)）时，从第k个点到达第j个点所需要的路径长度。

（3）dp数组初始化： dp[1][0] = 0，表示走入初始点0时，此时的距离出发点的距离为0。

（4）遍历顺序： 从左到右，从上到下

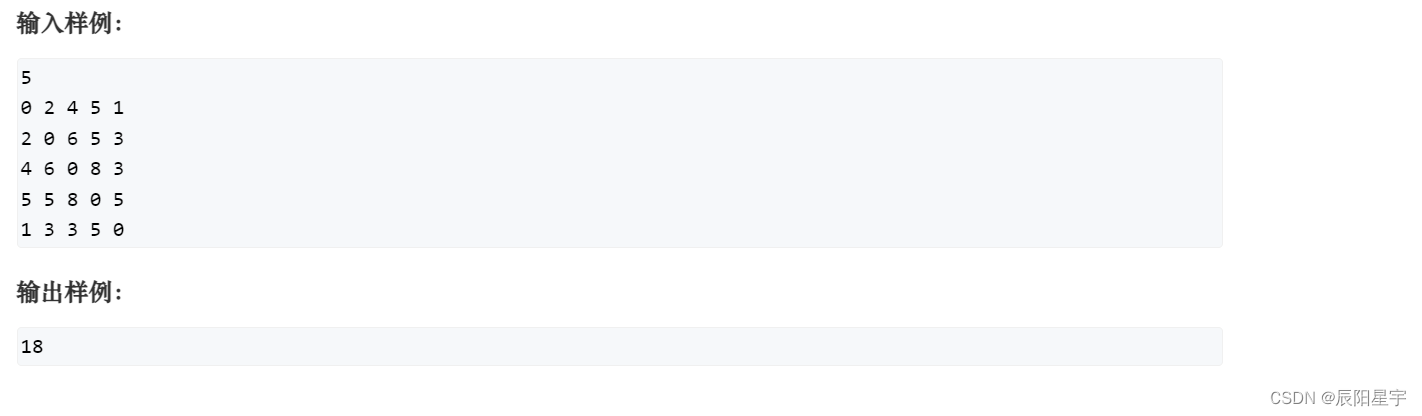
（5）举例：
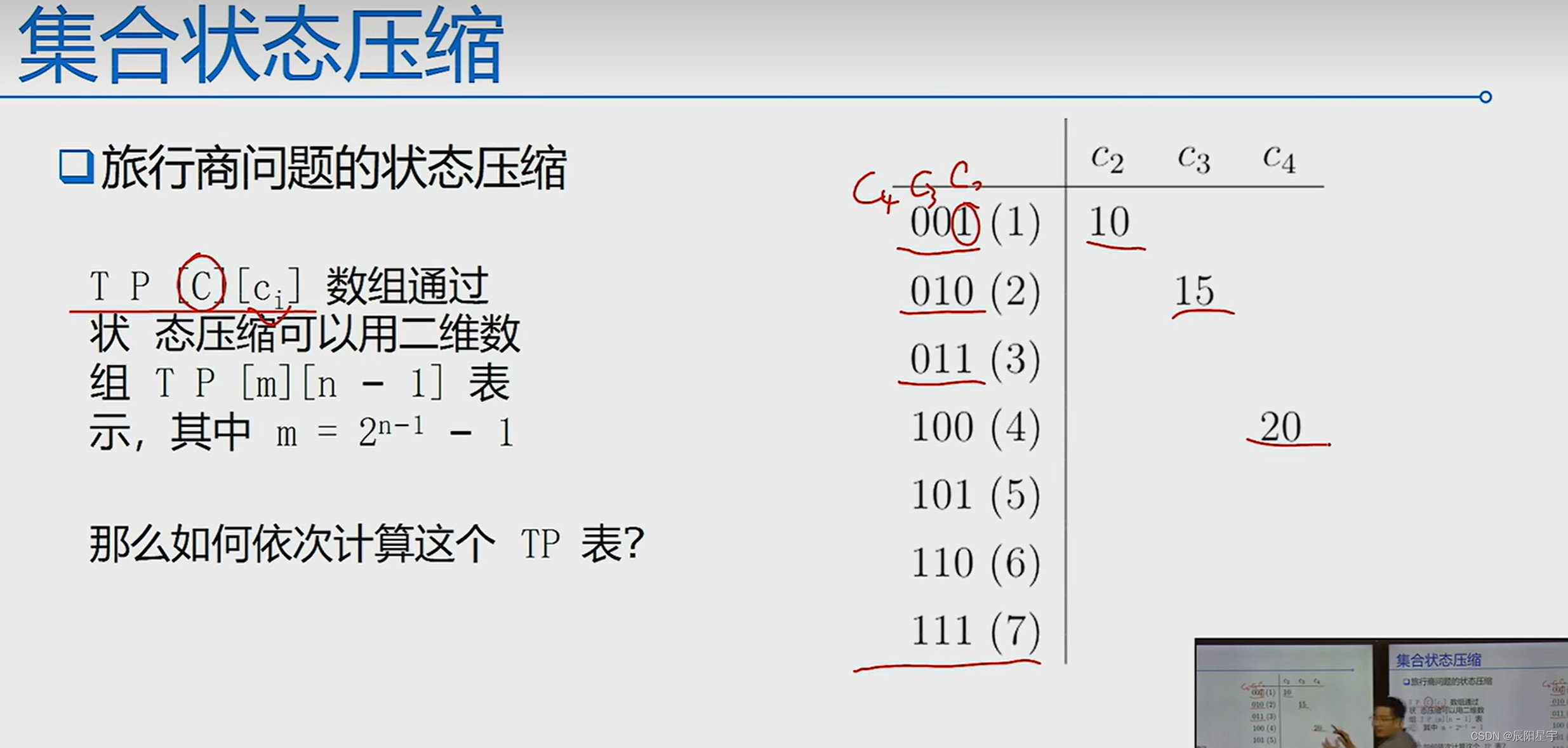
在这里插入图片描述

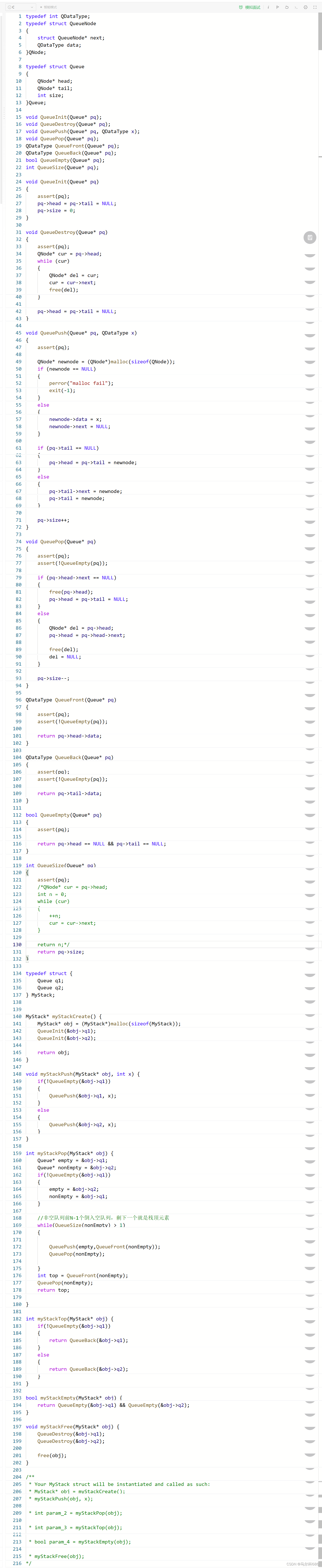
实现代码

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;
const int N = 21, M = 1 << N;
int dp[M][N], w[N][N];          // dp[M][N]：M表示二进制状态（某一位为0代表此位对应的点不走，为1代表此位对应的点走入）
int n;


int main() {
    // 1、输入数据
    cin >> n;
    for(int i = 0; i < n; i++) {
        for(int j = 0; j < n; j++) {
            cin >> w[i][j];
        }
    }
    
    // 2、初始化dp
    memset(dp, 0x3f, sizeof dp);        // 要求最小值，所以预先都初始化为最大值
    dp[1][0] = 0;                       // i=1：走入起始点，j=0：代表位于原点0
    
    // 3、状态计算
    for(int i = 0; i < 1 << n; i++) {             // 先遍历各个状态
        for(int j = 0; j < n; j++) {                // 再在遍历在状态i下，各点的最短路径情况
            if(i >> j & 1) {                      // 查看第j个点是否走入。i >> j & 1：将i左移j位，判定当前位置是否走入。为1表示走入，为0表示不走入
                for(int k = 0; k < n; k++) {        // 遍历从k到j的情况
                    // 查看能否由k走到j
                    if(i - (1 << j) >> k & 1) {  // （i - 1 << j）>> k : 在状态i中去除掉第j个点对应的走入状态后，右移k位。再和1相与，相当于是判定第k位是否存在，并能否由k走到j        
                        dp[i][j] = min(dp[i][j], dp[i - (1 << j)][k] + w[k][j]);    
                    }
                }
            }

        }
    }
    
    // 4、输出结果
    cout << dp[(1 << n) - 1][n - 1] << endl;        // 1 << n - 1：此时的值为11..11，意思为所有的点都走到，n - 1：代表走到第n - 1个点
    
    return 0;
}