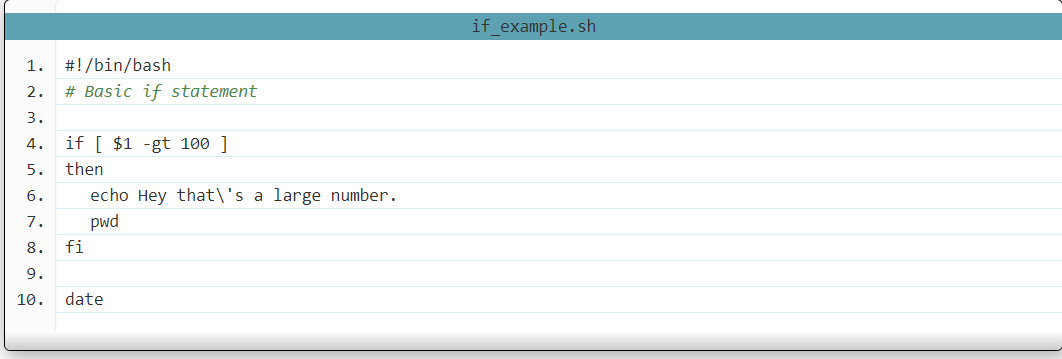
数列的极限的定义：

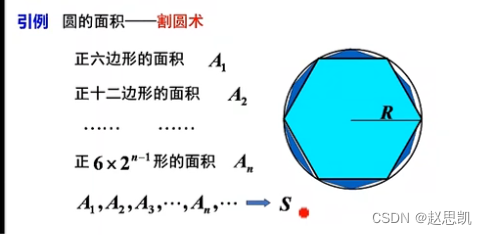
 当正多边形的边数越来越多时，正多边形的面积越来越接近于圆的面积。

这个过程就叫做极限。

数列的形式：

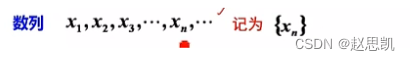
 数列的每一个下标对应一个数列元素值。

认识数列

这就是4个数列的表现形式。

 当数列的下标无限增长时，数列能否无限接近于一个确定的值？

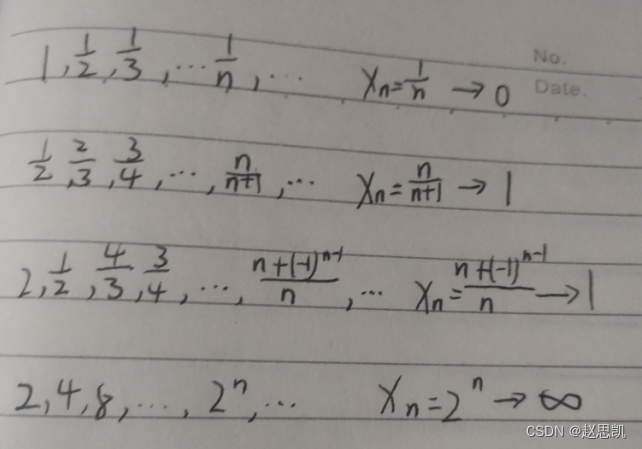
 我们根据例子1来讲解数列的极限：

 数列极限的定义：

 我们先分析数列极限的几何定义：

 落在领域中的无限项全部无限接近于极限值。

 分析现实意义：

 

 这两个数列有什么关系吗？

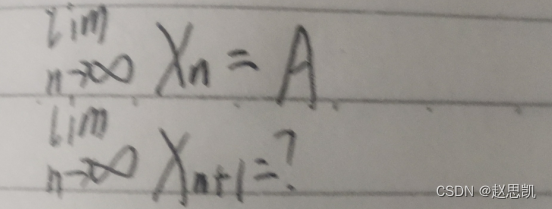
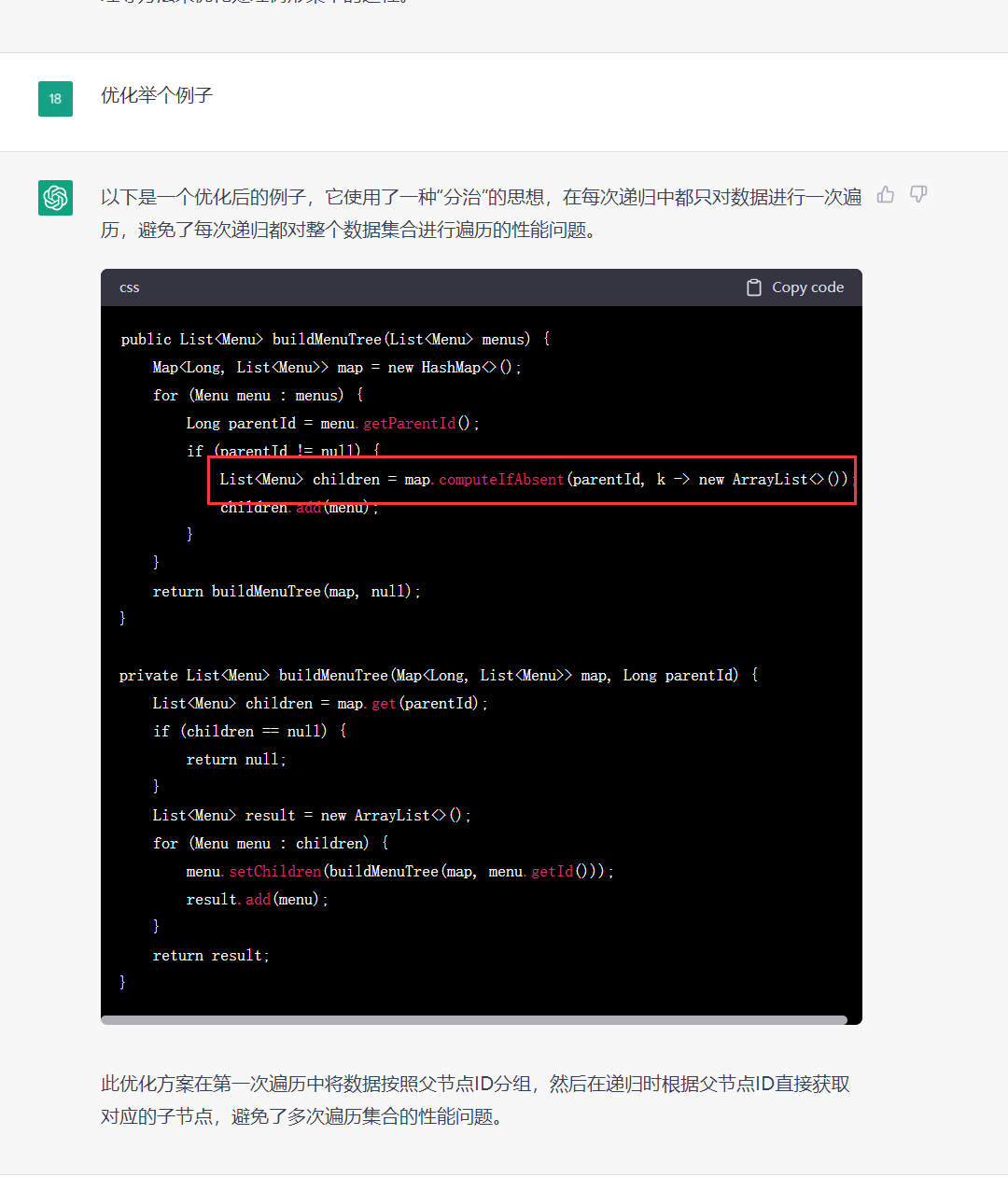
第二个数列实际上就是第一个数列舍弃掉首项之后的数列，所以数列Xn+1的极限值也为A，前面有限项的元素个数对极限值没有任何影响。

 例题1：

 我们进行证明：

收敛数列的性质：

唯一性：

一个数列只有一个极限值

如何证明，我们用反证法：

有界性：

有界性的定义：

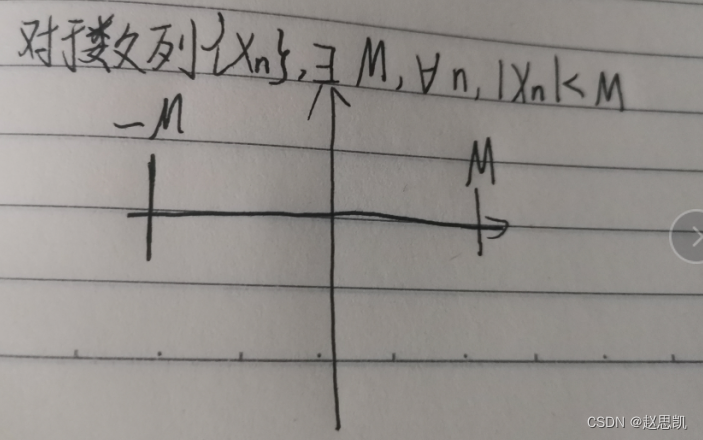
数列中的所有元素全部属于(-M,M)之间。

 有界性：收敛数列必有界。

 有界数列必然收敛吗？

错，我们举一个反例：

 保号性：

如果数列的极限值大于0，一定存在一个N，使N之后的所有元素全部大于0.

 我们进行证明：

 推论：

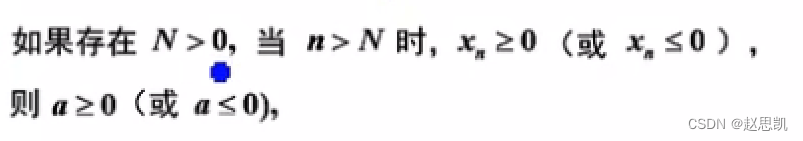
 我们使用反证法：

 这种写法可以吗？

 我们把大于号换成等于可以吗？

答：不可以，我们举出一个反例：

 

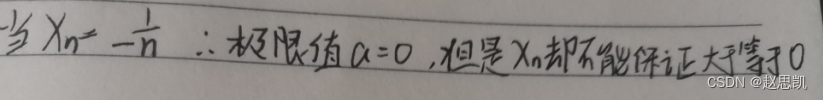
那这种写法呢？

答：不可以，我们举出一个反例：

 

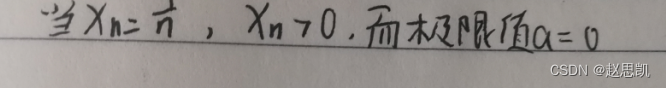
 收敛数列与子列之间的关系：

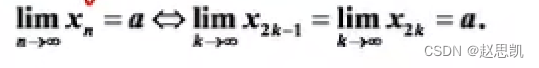
 数列Xn的极限值为a的充要条件是该数列的奇数列和偶数列的极限值都为a。