电子技术——晶体管尺寸
在本节我们介绍关于IC设计的一个重要的参数晶体管尺寸(例如长度和长宽比)。我们首先考虑MOS反相器。
反相器尺寸
为了说明 ( W / L ) (W/L) (W/L) 的尺寸大小以及 ( W / L ) p (W/L)_p (W/L)p 和 ( W / L ) n (W/L)_n (W/L)n 的比例问题对于MOS的性能问题。
- 为了缩小尺寸,所有沟道的长度在工艺允许的情况下应该设计成一样以来缩小IC尺寸。
- 对于给定的反相器,如果我们希望严格减小最小面积,则 ( W / L ) n (W/L)_n (W/L)n 通常选择为 1 到 1.5 。对于 ( W / L ) p (W/L)_p (W/L)p 的选择相对于 ( W / L ) n (W/L)_n (W/L)n 会影响噪声容限和 t P L H t_{PLH} tPLH 。设计师应该优化 Q P Q_P QP 和 Q N Q_N QN 的匹配问题,我们之前知道越好的匹配就会造成IC硅面积的浪费而且还会增加有效的容抗 C C C ,所以尽管 t P L H = t P H L t_{PLH} = t_{PHL} tPLH=tPHL 此时两个值均大于没有完美匹配的情况。因此选择 ( W / L ) p = ( W / L ) n (W/L)_p = (W/L)_n (W/L)p=(W/L)n 是一种选择,但是 ( W / L ) p = 2 ( W / L ) n (W/L)_p = 2(W/L)_n (W/L)p=2(W/L)n 通常是在权衡利弊的情况下的一种更优的选择。
- 解决完 ( W / L ) p (W/L)_p (W/L)p 和 ( W / L ) n (W/L)_n (W/L)n 的比例匹配问题,我们需要选择 ( W / L ) n (W/L)_n (W/L)n 来减小 t P t_P tP 从而提高数字系统的响应时间。增加 ( W / L ) n (W/L)_n (W/L)n 就会增加MOS的面积,进而导致电容 C C C 的增加。为了更精确的说明,我们将 C C C 表示为 C = C i n t + C e x t C = C_{int} + C_{ext} C=Cint+Cext 其中 C i n t C_{int} Cint 是MOS管的内部电容,而 C e x t C_{ext} Cext 是MOS的外部电容,包括线间电容和负载输入容抗。
增加MOS的长宽比 W / L W/L W/L 为最小尺寸反相器的 S S S 倍,会导致:
C = S C i n t 0 + C e x t C = SC_{int0} + C_{ext} C=SCint0+Cext
这里 C i n t 0 C_{int0} Cint0 是最小尺寸反相器的内部电容。
现在,若我们使用RC方法计算 t P t_P tP ,等效的电阻为:
R e q = 1 2 ( R N + R P ) R_{eq} = \frac{1}{2}(R_N + R_P) Req=21(RN+RP)
那么:
t P = 0.69 R e q C t_P = 0.69R_{eq}C tP=0.69ReqC
若我们定义最小尺寸反相器的等效电阻为 R e q 0 R_{eq0} Req0 ,增加MOS的长宽比 W / L W/L W/L 为最小尺寸反相器的 S S S 倍会导致:
R e q = R e q 0 / S R_{eq} = R_{eq0} / S Req=Req0/S
带入所有的表达式可以得到:
t P = 0.69 ( R e q 0 S ) ( S C i n t 0 + C e x t ) = 0.69 ( R e q 0 C i n t 0 + 1 S R e q 0 C e x t ) t_P = 0.69(\frac{R_{eq0}}{S}) (SC_{int0} + C_{ext}) = 0.69(R_{eq0}C_{int0} + \frac{1}{S} R_{eq0}C_{ext}) tP=0.69(SReq0)(SCint0+Cext)=0.69(Req0Cint0+S1Req0Cext)
这说明放大比例 S S S 并不会影响内部电容对于 t P t_P tP 的影响,然而,会降低外部电容的分量值。我们可以使用上式来选择一个合适的 S S S 来将 t P t_P tP 保持在最小值,同时要注意增加 S S S 会增加MOS的硅面积。
CMOS逻辑门中的晶体管尺寸
当决定使用CMOS电路的时候,唯一的重要的事情就是决定所有器件的 W / L W/L W/L 比例。最好情况下,我们必须让CMOS逻辑门电路的电流驱动能力必须等于相同的反相器的电流驱动能力。对于基本反相器,我们记 ( W / L ) n = n (W/L)_n = n (W/L)n=n 并且 ( W / L ) p = p (W/L)_p = p (W/L)p=p ,这里 n = 1 ≃ 1.5 n = 1 \simeq 1.5 n=1≃1.5 ,对于匹配设计 p = ( μ n / μ p ) n p = (\mu_n/\mu_p) n p=(μn/μp)n 通常 p = 2 n p = 2n p=2n 对于最小尺寸设计 p = n p = n p=n 。因此,我们在设计PDN的时候,我们必须选择每一个MOS的长宽比让其PDN的泄放电流能力至少等于一个 W / L = n W/L = n W/L=n 的NMOS的泄放电流能力。同样的对于PUN来说,我们必须选择每一个MOS的长宽比让其PUN的提供电流能力至少等于一个 W / L = p W/L = p W/L=p 的PMOS的提供电流能力。这保证了逻辑门电路延迟的最坏情况——等同于基本反相器。
基于上述的讨论,我们必须强调“最坏情况”是什么。这意味着,我们在选择晶体管尺寸的时候,我们需要找到一种输入的组合方式使得最低输出电流等于基本反相器的电流。在我们讨论具体的例子之前,我们首先要解决如何决定多个MOS管组合逻辑门电路的电流的驱动能力,也就是找到等价单个MOS W / L W/L W/L 的值。首先我们考虑MOS串联和并联时候的情况。
基于 R o n R_{on} Ron 与 W / L W/L W/L 反比的事实,若多个MOS管串联,每个MOS的宽长比分别为 ( W / L ) 1 , ( W / L ) 2 , … (W/L)_1,(W/L)_2,\ldots (W/L)1,(W/L)2,… 等价的电阻为:
R s e r i e s = R N 1 + R N 2 + … = c o n s t ( W / L ) 1 + c o n s t ( W / L ) 2 + … = c o n s t [ 1 ( W / L ) 1 + 1 ( W / L ) 2 + … ] = c o n s t ( W / L ) e q R_{series} = R_{N1} + R_{N2} + \ldots = \frac{const}{(W/L)_1} + \frac{const}{(W/L)_2} + \ldots = const[\frac{1}{(W/L)_1} + \frac{1}{(W/L)_2} + \ldots] = \frac{const}{(W/L)_{eq}} Rseries=RN1+RN2+…=(W/L)1const+(W/L)2const+…=const[(W/L)11+(W/L)21+…]=(W/L)eqconst
那么等价的长宽比为:
( W / L ) e q = 1 1 ( W / L ) 1 + 1 ( W / L ) 2 + … (W/L)_{eq} = \frac{1}{\frac{1}{(W/L)_1} + \frac{1}{(W/L)_2} + \ldots} (W/L)eq=(W/L)11+(W/L)21+…1
同样的方法,能够导出并联时候的情况:
( W / L ) e q = ( W / L ) 1 + ( W / L ) 2 + … (W/L)_{eq} = (W/L)_1 + (W/L)_2 + \ldots (W/L)eq=(W/L)1+(W/L)2+…
现在,考虑下图的一个四变量输入的或非门:
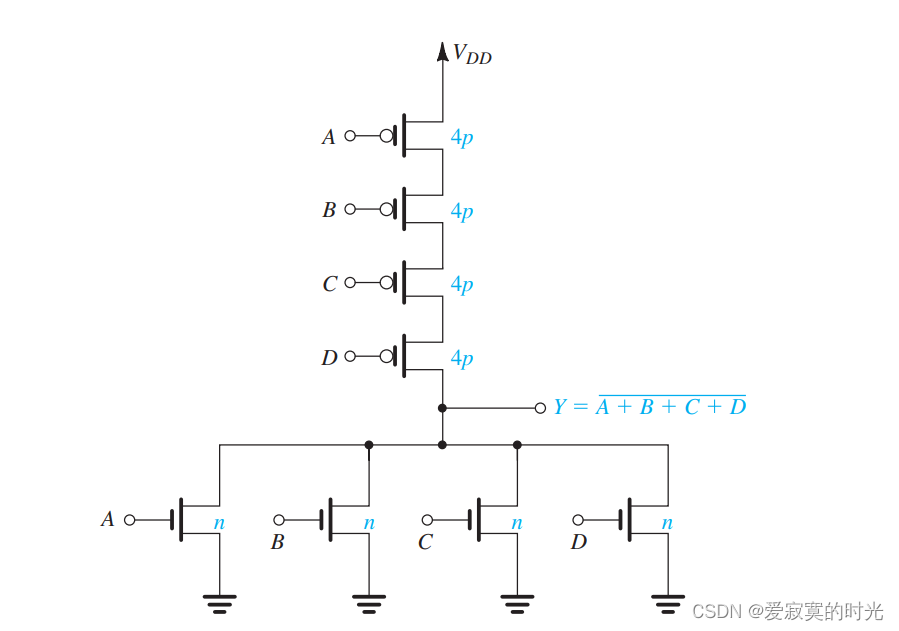
其中对于PDN来说,最坏的情况(最小电流)是四个NMOS只有一个导通,因此,我们对于每一个NMOS都选择
W
/
L
=
n
W/L = n
W/L=n 即可。对于PUN来说最坏的情况(也是唯一的情况)是四个PMOS均导通,根据串联MOS公式,我们让每个PMOS的
W
/
L
=
4
p
W/L = 4p
W/L=4p 即可。
另外一个例子是四变量输入的与非门,如图:
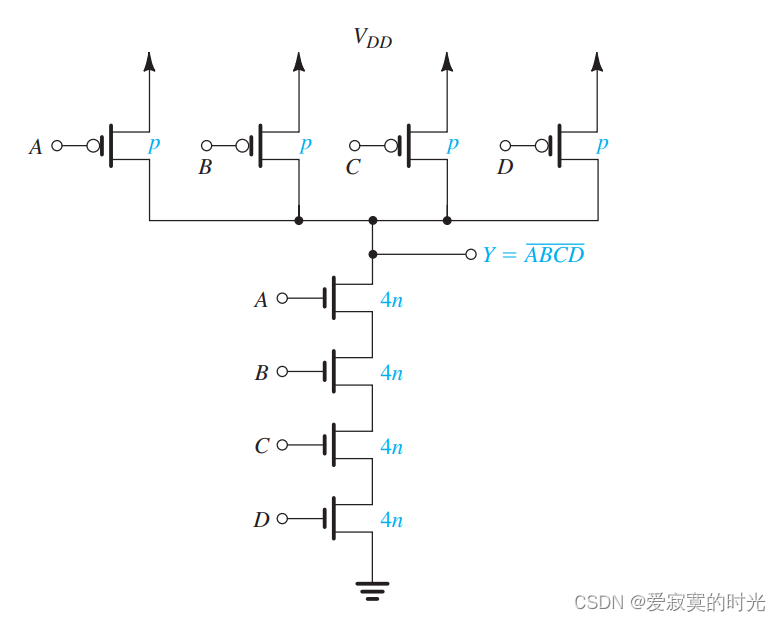
需要注意的是,通常
p
p
p 是
n
n
n 的2到3倍,因此或非门的体积要大于与非门的体积。基于此原因,设计师更愿意使用NAND来实现组合逻辑。
扇入扇出效应与传播延迟
每一个CMOS们电路的每一个输入变量都需要提供给两个晶体管,一个NMOS和一个PMOS。相比于另外一种只需要一种输入链接到一个晶体管的MOS逻辑门电路来说,例如伪NMOS逻辑门电路,额外的晶体管不仅增加了芯片的面积,而且还增加总有效阻抗从而增加了传播延迟。增加MOS的宽长比可以在一定程度上补偿这种传播延迟。特别的,通过增大元件的尺寸,我们可以保留电流驱动能力,然而却增加了总有效容抗。因此 t P t_P tP 仍然会受到扇入数的影响,扇入数指的实际的接入晶体管数量,例如NAND的扇入数是4。如果需要更多的输入变量,明智的电路设计者会通过巧妙的变换或者设计让输入变量的个数不超过4个。这通常意味着需要增加联级的数量,这同样会增加传播延迟。然而,相比之下,这种方法的传播延迟增加总比之前未优化的情况要小。
同样的,对于扇出数来说,其直接关系到负载的容抗,因此扇出数越大,则负载的容抗越大,传播延迟越大。
因此尽管CMOS有许多优点,当扇入和扇出数增加的时候,同样会受到电路复杂性的影响,导致芯片面积和传播延迟的增加。
驱动大电容
在一些特别的CMOS电路中,需要驱动较大的容性负载。例如,在IC中较长的走线,或是需要通过片外PCB走线的信号,此时的容抗要比普通情况下的容抗大上百倍。
我们需要一种在可以忍受的传播延迟下驱动大容抗的方法。下图展示了一个标准反相器驱动电容 C L C_L CL 的演示图:
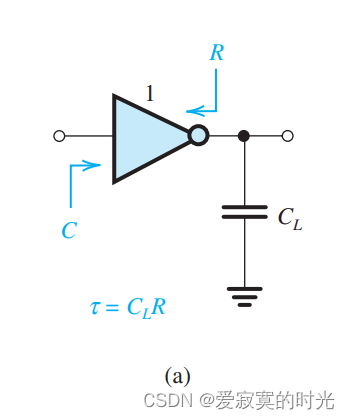
上面的模型,我们简单的总结为从输入端看过去容值为 C C C 等效电容为 R R R 的CR模型,因为 C L C_L CL 为负载容抗,根据估算:
t P = τ = C L R t_P = \tau = C_LR tP=τ=CLR
延迟将会非常大。
一种解决方法是,放大反相器的体积,如图:
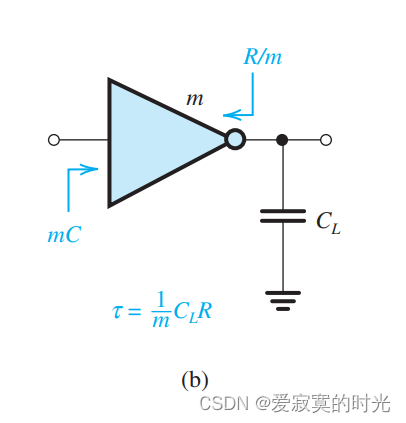
这里的反相器是参考反相器的
m
m
m 倍,此时输出电阻将会是
R
/
m
R/m
R/m ,此时的传播延迟为:
τ = C L ( R / m ) \tau = C_L(R/m) τ=CL(R/m)
传播延迟将会降低 m m m 倍,但是这并不是一个方法。观察到输入的容抗变成了原来的 m m m 倍,这需要一个更大的反相器来驱动他,并没从根本上解决问题,而是把负担交给了其他反相器。
但是,这种方法给我们了一种解决问题的思路,即使用联级反相器,如图:
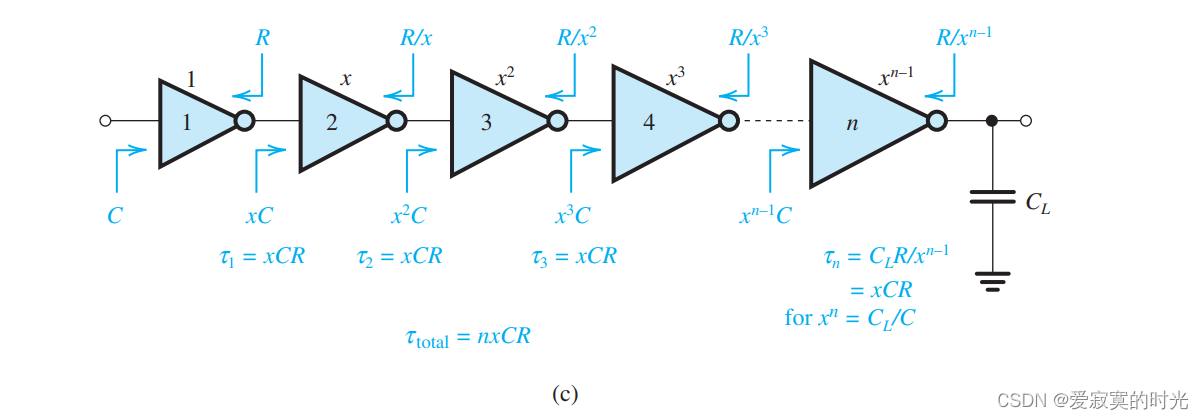
观察上图,我们发现反相器的尺寸成等比数列,我们发现每一级之间的传播延迟都为:
τ = x C R \tau = xCR τ=xCR
特别的,可以证明当满足:
τ n ≡ C L ( R x n − 1 ) = x C R \tau_n \equiv C_L(\frac{R}{x^{n-1}}) = xCR τn≡CL(xn−1R)=xCR
的时候,也就是:
x n = C L C x^n = \frac{C_L}{C} xn=CCL
整体延迟最小为:
t P = τ t o t a l = n x C R t_P = \tau_{total} = nxCR tP=τtotal=nxCR
问题是如何选定 x x x 和 n n n 。在数学中可以证明,当 x = e ≃ 2.718 x = e \simeq 2.718 x=e≃2.718 的时候,传播延迟最小。实际上,在2.5-4之间都可以提升性能。