线性表的应用

线性表的合并

问题描述：

假设利用两个线性表L_a和L_b表示两个集合A和B，现要求一个新的集合A=A∪B

即：

L_a=(7,5,3,11) L_b=(2,6,3) A=(7,8,3,11,2,6)

算法步骤（A既是参数，也是操作的结果）

• 依次（需要循环）取出L_b中的每个元素
• 在L_a中查找该元素如果没有，插入到L_a表尾

List union(List a, List b)
{
	List L = (List)malloc(sizeof(List));
	La_len = ListLength(a);
	Lb_len = ListLength(b);
	for (int i = 1; i < Lb_len, i++)
	{
		GetElem(Lb, i, e);  //获取Lb上的第i个元素给e
		if (!LocateElem(La, e))//寻找La上有没有相同元素
		{//如果没有
			insertList_tail(List a, ++La_len, e);;
		}
	}

}

这里的算法是通过用与La Lb的具体存储方式无关（不关心他们是顺序表还是链表）

算法复杂度是两线性表表长的乘积

有序表的合并

问题描述：

已知线性表L_a和L_b中的数据元素按值非递减有序排列，现要求将L_a和L_b归并为一个新的线性表L_c ，且L_c中的数据元素仍按值非递减有序排列。

L_a=(1,7,8) L_b=(2,4,6,8,10,11) L_c =(1,2,4,6,7,8,8,10,11)

• 创建一个空表Lc
• 依次从La或Lb中摘取元素值较小的结点插入到Lc表的最后，知道其中一个表为空为止
• 继续将La或Lb其中一个表的剩余结点插入在Lc表的最后

循环比较-小的值放入Lc-移动小的元素所在数组的指针和Lc指针

**[复习]**数组名即数组的首地址是常量

nt a[10];

int *p=a;/*int *p;p=a而p=a与p=&a[0]等价*/

如果指针变量p已指向数组中的一个元素，则p+1指向同一数组中的下一个元素如果p的初值为&a[0],则：p+i和a+i 就是 a[i]的地址,*(p+i)即为a[i]

引用一个数组元素可以用：

1. 下标法，即用 a[i]形式访问数组元素。在前面介绍数组时都是采用这种方法。
2. 指针法，即采用(a+i)或(p+i)形式，用间接访问的方法来访问数组元素

自增运算++在后先用后加=>*pc=*pa;pa++;pc++

指针到达尾指针达到表尾指针<尾指针未到表尾而有一个到达表尾就停止判断

算法时间复杂度两表表长之和

算法的空间复杂度两表表长之和

下标/索引

2.链表实现

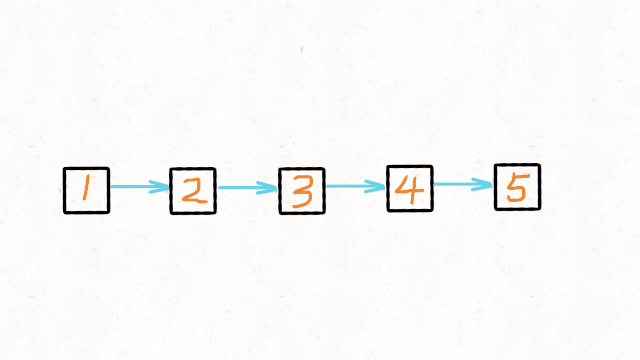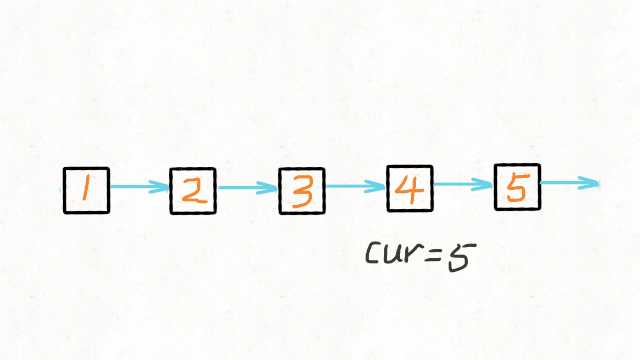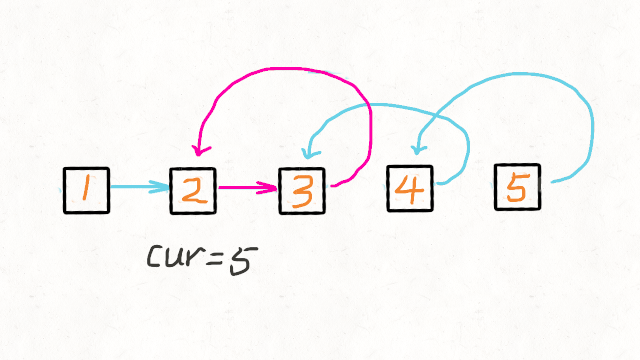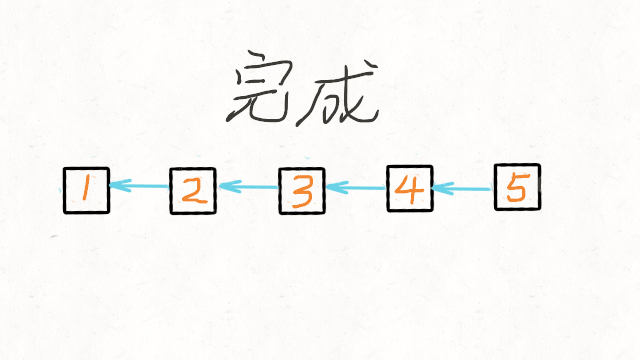
Lc仍是带表头结点的单链表在La和Lb的表头结点中任选一个(这里我们选La的头结点作为Lc的头结点Lc=La)

当然像La和Lb一样Lc同样需要一个pc

（比较大小）1<2即pa->datadata=>pa指向的结点插入到pc后(pc->next=pa)(而pc指向当前表尾(pc=pa;)且移动pa(pa=pa->next;)小的元素插入到pc后移动pc指向当前表尾移动小元素所在链表的指针)直到一个链表中所有元素都插入到Lc中

（pa？pc->next=pb:pc->next=pa;）