第十四届蓝桥杯第三期模拟赛 【python】

✨最小的十六进制（python的16进制）

❓️问题描述

请找到一个大于 2022 的最小数，这个数转换成十六进制之后，所有的数位（不含前导 0）都为字母（A 到 F）。
请将这个数的十进制形式作为答案提交。

答案提交

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

🧠思路

这道题和第一期模拟赛的第一题都是考虑到了二进制，对于python来说，还是很快的，只需要从2022开始遍历，利用python的bin函数，就可以迅速将十进制转成二进制，然后再减去首字母的两个0b即可，判断最低的6个尾数为0即可。

🖥︎参考答案

2730

i = 2023 # 从大于2022的数开始遍历
while True:
    s = hex(i)[2:] # 转化为16进制
    if s.isalpha(): # 如果全是字母返回true
        print(i,s) # 2730 aaa
        break
    i += 1

✨Excel的列（进制转化）

❓️问题描述

在 Excel 中，列的名称使用英文字母的组合。前 26 列用一个字母，依次为 A 到 Z，接下来 26*26 列使用两个字母的组合，依次为 AA 到 ZZ。

请问第 2022 列的名称是什么？

答案提交

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

🧠思路

如果以2个字母的组合为列名，最多为26x26=676个列，所以2022列就是以三个字母的组合去得到的，其实简单一点这道题也可以进行简单的手算，但是仔细一看，实际上就是2022转成26进制即可，但是这个26进制没有数字，是从A~Z。

其实这道题，我们也可以列一个数组，穷举把所有数算出来，然后取对应位置2022的数据出来就好了，这两种方法都OK的。

🖥︎参考答案

BYT

转化为26进制

def to_base_26(num):
    """
    Convert an integer to base 26.
    """
    if num == 0:
        return 'A' # 如果为0 
    
    letters = []
    while num > 0:
        num, rem = divmod(num, 26)
        letters.append(chr(ord('A') + rem - 1)) 
    
    return ''.join(reversed(letters)) # 进行翻转

print(to_base_26(2022))

穷举法

def get(x, y, z):
    return x * 26 * 26 + y * 26 + z

def ans(x, y, z):
    s = ''
    s += chr(ord('A') + x - 1)
    s += chr(ord('A') + y - 1)
    s += chr(ord('A') + z - 1)
    return s

n = 2022

for i in range(1, 27):
    for j in range(1, 27):
        for k in range(1, 27):
            if get(i, j, k) == n:
                print(ans(i, j, k))
                exit()

✨相等日期（datetime日期）

❓️问题描述

对于一个日期，我们可以计算出年份的各个数位上的数字之和，也可以分别计算月和日的各位数字之和。请问从 1900 年 1 月 1 日至 9999 年 12 月 31 日，总共有多少天，年份的数位数字之和等于月的数位数字之和加日的数位数字之和。

例如，2022年11月13日满足要求，因为 2+0+2+2=(1+1)+(1+3) 。

请提交满足条件的日期的总数量。

答案提交

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

🧠思路

这道题最简单的话，就是可以利用python的datetime库进行判断，转成字符串进行计数，最后把符合条件的结果计数输出就是最后日期的总数量。

🖥︎参考答案

70910

import datetime
start = datetime.date(1900,1,1)
end = datetime.date(9999,12,31)

# 把字符串转为会数字，2022转化为2+0+2+2=6
def get_num(n):
    return sum([int(i) for i in str(n)])
 
cnt = 0
while start < end:
    y,m,d = start.year, start.month, start.day
    if get_num(y) == get_num(m) + get_num(d):
        cnt += 1
    start += datetime.timedelta(days=1)

print(cnt) # 70910

✨多少种取法（简单模拟）

❓️问题描述

小蓝有 30 个数，分别为：99, 22, 51, 63, 72, 61, 20, 88, 40, 21, 63, 30, 11, 18, 99, 12, 93, 16, 7, 53, 64, 9, 28, 84, 34, 96, 52, 82, 51, 77

小蓝可以在这些数中取出两个序号不同的数，共有 30*29/2=435 种取法。
请问这 435 种取法中，有多少种取法取出的两个数的乘积大于等于 2022 。

答案提交

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

🧠思路

这道题其实很简单的，就是随机取两个数，然后进行判断，如果符合条件的话计数，最后就把结果输出即可

🖥︎参考答案

189

nums = [0, 99, 22, 51, 63, 72, 61, 20, 88, 40,
	21, 63, 30, 11, 18, 99, 12, 93, 16, 7, 53,
	64, 9, 28, 84, 34, 96, 52, 82, 51, 77]

cnt = 0
for i in range(1,31):
    for j in range(i+1,31):
        if nums[i]*nums[j] >= 2022: # >=2022
            cnt += 1
print(cnt) # 189

✨最大连通分块（DFS）

❓️问题描述

小蓝有一个 30 行 60 列的数字矩阵，矩阵中的每个数都是 0 或 1 。如果从一个标为 1 的位置可以通过上下左右走到另一个标为 1 的位置，则称两个位置连通。与某一个标为 1 的位置连通的所有位置（包括自己）组成一个连通分块。
请问矩阵中最大的连通分块有多大？

110010000011111110101001001001101010111011011011101001111110
010000000001010001101100000010010110001111100010101100011110
001011101000100011111111111010000010010101010111001000010100
101100001101011101101011011001000110111111010000000110110000
010101100100010000111000100111100110001110111101010011001011
010011011010011110111101111001001001010111110001101000100011
101001011000110100001101011000000110110110100100110111101011
101111000000101000111001100010110000100110001001000101011001
001110111010001011110000001111100001010101001110011010101110
001010101000110001011111001010111111100110000011011111101010
011111100011001110100101001011110011000101011000100111001011
011010001101011110011011111010111110010100101000110111010110
001110000111100100101110001011101010001100010111110111011011
111100001000001100010110101100111001001111100100110000001101
001110010000000111011110000011000010101000111000000110101101
100100011101011111001101001010011111110010111101000010000111
110010100110101100001101111101010011000110101100000110001010
110101101100001110000100010001001010100010110100100001000011
100100000100001101010101001101000101101000000101111110001010
101101011010101000111110110000110100000010011111111100110010
101111000100000100011000010001011111001010010001010110001010
001010001110101010000100010011101001010101101101010111100101
001111110000101100010111111100000100101010000001011101100001
101011110010000010010110000100001010011111100011011000110010
011110010100011101100101111101000001011100001011010001110011
000101000101000010010010110111000010101111001101100110011100
100011100110011111000110011001111100001110110111001001000111
111011000110001000110111011001011110010010010110101000011111
011110011110110110011011001011010000100100101010110000010011
010011110011100101010101111010001001001111101111101110011101

答案提交

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

🧠思路

这道题是一道

🖥︎参考答案

148

import sys
sys.setrecursionlimit(1<<31-1)

matrix = '''110010000011111110101001001001101010111011011011101001111110
010000000001010001101100000010010110001111100010101100011110
001011101000100011111111111010000010010101010111001000010100
101100001101011101101011011001000110111111010000000110110000
010101100100010000111000100111100110001110111101010011001011
010011011010011110111101111001001001010111110001101000100011
101001011000110100001101011000000110110110100100110111101011
101111000000101000111001100010110000100110001001000101011001
001110111010001011110000001111100001010101001110011010101110
001010101000110001011111001010111111100110000011011111101010
011111100011001110100101001011110011000101011000100111001011
011010001101011110011011111010111110010100101000110111010110
001110000111100100101110001011101010001100010111110111011011
111100001000001100010110101100111001001111100100110000001101
001110010000000111011110000011000010101000111000000110101101
100100011101011111001101001010011111110010111101000010000111
110010100110101100001101111101010011000110101100000110001010
110101101100001110000100010001001010100010110100100001000011
100100000100001101010101001101000101101000000101111110001010
101101011010101000111110110000110100000010011111111100110010
101111000100000100011000010001011111001010010001010110001010
001010001110101010000100010011101001010101101101010111100101
001111110000101100010111111100000100101010000001011101100001
101011110010000010010110000100001010011111100011011000110010
011110010100011101100101111101000001011100001011010001110011
000101000101000010010010110111000010101111001101100110011100
100011100110011111000110011001111100001110110111001001000111
111011000110001000110111011001011110010010010110101000011111
011110011110110110011011001011010000100100101010110000010011
010011110011100101010101111010001001001111101111101110011101'''

matrix = matrix.split('\n')

matrix = list(map(list,matrix))

n,m = len(matrix), len(matrix[0])

f = [(-1,0),(1,0),(0,-1),(0,1)]

def dfs(x,y):
    global cnt
    matrix[x][y] = '0'
    cnt += 1
    for fx,fy in f:
        nx,ny = x + fx, y + fy
        if 0<=nx<n and 0<=ny<m and matrix[nx][ny] == '1':
            dfs(nx,ny) # 进行深搜
        
ans = 0
for i in range(n):
    for j in range(m):
        if matrix[i][j] == '1':
            cnt = 0 # 求取连通分量
            dfs(i,j) 
            ans = max(ans,cnt) # 取最大连通分量
print(ans)

✨哪一天（模拟题）

❓️问题描述

给定一天是一周中的哪天，请问 n 天后是一周中的哪天？

输入格式

输入第一行包含一个整数 w，表示给定的天是一周中的哪天，w 为 1 到 6 分别表示周一到周六，w 为 7 表示周日。

第二行包含一个整数 n。

输出格式

输出一行包含一个整数，表示 n 天后是一周中的哪天，1 到 6 分别表示周一到周六，7 表示周日。

样例输入

6
10

样例输出

2

评测用例规模与约定

对于所有评测用例，$1<=n<=1000000$。

🧠思路

这道题实际上就是模拟题，首先我们可以认为是0~6分别代表周一到周日，我们只需要把（当前星期+n天数%7）就可以得到n天后是周几，由于是0-indexing的，所以+1转成1-indexing

🖥︎参考代码

w = int(input())
n = int(input())

print((w-1+n)%7+1)

✨信号覆盖（暴力模拟）

❓️问题描述

小蓝负责一块区域的信号塔安装，整块区域是一个长方形区域，建立坐标轴后，西南角坐标为 (0, 0)， 东南角坐标为 (W, 0)， 西北角坐标为 (0, H)， 东北角坐标为 (W, H)。其中 W, H 都是整数。

他在 n 个位置设置了信号塔，每个信号塔可以覆盖以自己为圆心，半径为 R 的圆形（包括边缘）。

为了对信号覆盖的情况进行检查，小蓝打算在区域内的所有横纵坐标为整数的点进行测试，检查信号状态。其中横坐标范围为 0 到 W，纵坐标范围为 0 到 H，总共测试 (W+1) * (H+1) 个点。

给定信号塔的位置，请问这 (W+1)*(H+1) 个点中有多少个点被信号覆盖。

输入格式

输入第一行包含四个整数 W, H, n, R，相邻整数之间使用一个空格分隔。
接下来 n 行，每行包含两个整数 x, y，表示一个信号塔的坐标。信号塔可能重合，表示两个信号发射器装在了同一个位置。

输出格式

输出一行包含一个整数，表示答案。

样例输入

10 10 2 5
0 0
7 0

样例输出

57

评测用例规模与约定

对于所有评测用例，1 <= W, H <= 100，1 <= n <= 100, 1 <= R <= 100, 0 <= x <= W, 0 <= y <= H。

🧠思路

这道题实际上一看下来，就是一个暴力模拟的题目了，只需要循环这（W+1)*(H+1)个点，查看有哪些被信号覆盖即可，所以这道题可以直接穷举，看题目的一个数量级不大，所以$O(n^3)$应该也是没问题的，我稍微改进了一下简单的穷举，我只对每一个信号塔周边的区域进行判断。

也可以遍历所有的点，然后遍历所有的信号塔查看是否有覆盖，但是那个可能就会代码简单，时间复杂一点

🖥︎参考代码

w,h,n,R = map(int,input().split())

def dist(x1,y1,x2,y2):
    return ((x1-x2)**2+(y1-y2)**2)**0.5

flag = [[0]*(h+1) for _ in range(w+1)] # flag[i][j]表示是否有记录过
cnt = 0
for k in range(n):
    x,y = map(int,input().split())
    for i in range(x-R,x+R+1):
        for j in range(y-R,y+R+1):
            if 0<=i<=w and 0<=j<=h and flag[i][j]==0 and dist(i,j,x,y) <= R:
                flag[i][j] = 1 # 标记代表已经记录过被覆盖了
                cnt += 1
print(cnt)

✨清理水草（简单模拟）

❓️问题描述

小蓝有一个 n * m 大小的矩形水域，小蓝将这个水域划分为 n 行 m 列，行数从 1 到 n 标号，列数从 1 到 m 标号。每行和每列的宽度都是单位 1 。

现在，这个水域长满了水草，小蓝要清理水草。

每次，小蓝可以清理一块矩形的区域，从第 r1 行（含）到第 r2 行（含）的第 c1 列（含）到 c2 列（含）。

经过一段时间清理后，请问还有多少地方没有被清理过。

输入格式

输入第一行包含两个整数 n, m，用一个空格分隔。

第二行包含一个整数 t ，表示清理的次数。

接下来 t 行，每行四个整数 r1, c1, r2, c2，相邻整数之间用一个空格分隔，表示一次清理。请注意输入的顺序。

输出格式

输出一行包含一个整数，表示没有被清理过的面积。

样例输入

2 3
2
1 1 1 3
1 2 2 2

样例输出

2

样例输入

30 20
2
5 5 10 15
6 7 15 9

样例输出

519

评测用例规模与约定

对于所有评测用例，1 <= r1 <= r2 <= n <= 100, 1 <= c1 <= c2 <= m <= 100, 0 <= t <= 100。

🧠思路

感觉这道题也是一样的，和前面的信号覆盖也是类似的，并且数据也不是很大，所以首先就用模拟的穷举也可以很快的写出来，只要把清理过的标为0，其他均为1，之后进行求和即可

所以以下简单的思路还是用一个flag数组表示是否清理过，然后计数所有清理过的草坪，最后总数-清理过的草坪就可以得到未清理过的草坪了。

🖥︎参考代码

w,h = map(int,input().split())
t = int(input())

flag = [[0]*(h+1) for _ in range(w+1)] # flag[i][j]代表是否清理过
cnt = 0
for _ in range(t):
    r1, c1, r2, c2 = map(int,input().split())
    for i in range(r1,r2+1):
        for j in range(c1,c2+1):
            if flag[i][j] == 0:
                flag[i][j] = 1
                cnt += 1 # 清理过的草坪+1
print(w*h-cnt) # 剩余未清理的草坪

✨最长滑行（DFS搜索）

❓️问题描述

小蓝准备在一个空旷的场地里面滑行，这个场地的高度不一，小蓝用一个 n 行 m 列的矩阵来表示场地，矩阵中的数值表示场地的高度。

如果小蓝在某个位置，而他上、下、左、右中有一个位置的高度（严格）低于当前的高度，小蓝就可以滑过去，滑动距离为 1 。

如果小蓝在某个位置，而他上、下、左、右中所有位置的高度都大于等于当前的高度，小蓝的滑行就结束了。

小蓝不能滑出矩阵所表示的场地。

小蓝可以任意选择一个位置开始滑行，请问小蓝最多能滑行多远距离。

输入格式

输入第一行包含两个整数 n, m，用一个空格分隔。

接下来 n 行，每行包含 m 个整数，相邻整数之间用一个空格分隔，依次表示每个位置的高度。

输出格式

输出一行包含一个整数，表示答案。

样例输入

4 5
1 4 6 3 1
11 8 7 3 1
9 4 5 2 1
1 3 2 2 1

样例输出

7

样例说明

滑行的位置一次为 (2, 1), (2, 2), (2, 3), (3, 3), (3, 2), (4, 2), (4, 3)。

评测用例规模与约定

对于 30 % 评测用例，$1<=n<=20,1<=m<=20$ ，$0<=高度<=100$ 。

对于所有评测用例，$1<=n<=100，1<=m<=100，0<=高度<=10000$ 。

🧠思路

这道题实际上就是一道搜索问题，本质上我们还是使用DFS进行求解，我们可以从任意一个点开始搜索，然后最后取最大值就是我们最后的结果。这里我们使用DFS求解，为了加快速度，我们还是使用了记忆化搜索，如果发现已经搜索过了，就直接返回结果即可。

首先简单讲一讲DFS的思路吧，我们会从当前x,y进行不断搜索，然后发现下一个点符合条件，在范围内且严格小于当前点的高度，我们就继续搜索，因为我们要取最长，所以我们要取max，不断取最优的结果，最后都记录到我们的dp数组中

这样在下一次搜索的时候，如果发现当前的dp数组的值已经被记录过了，那我们就直接返回值即可，就不需要那么多花里胡哨的操作，其实这道题可能也叫树形的DFS，有时候还是会出现的，不过思路还是OK的，就是类似于树形一样不断迭代dfs而已，最后就是还要加上这个递归深度的代码，这样保证自己不会出错！！！

🖥︎参考代码

import sys
sys.setrecursionlimit(1<<31-1) # 设置最大的递归深度

n,m = map(int,input().split())
a = []
for _ in range(n):
    a.append(list(map(int,input().split())))

dp = [[-1]*m for _ in range(n)] # 记忆化搜索

f = [(-1,0),(1,0),(0,-1),(0,1)]

# 返回从x,y开始的最长距离
def dfs(x,y):
    if dp[x][y] != -1: return dp[x][y] # 如果说明不为-1，说明已经记录过了，直接返回即可
    res = 1
    for fx,fy in f:
        nx,ny = x+fx,y+fy
        if 0<=nx<n and 0<=ny<m and a[x][y] > a[nx][ny]:
            # dfs(nx,ny)代表从ny,ny的最长距离
            res = max(res,dfs(nx,ny) + 1) # 不断取最优的
    dp[x][y] = res # 记录当前值
    return dp[x][y]

ans = 0
for i in range(n):
    for j in range(m):
        ans = max(ans, dfs(i,j))
print(ans)

✨区间最小值（ST表模板题）

❓️问题描述

小蓝有一个序列 $a[1],a[2],\dots ,a[n]$。

给定一个正整数 k，请问对于每一个 1 到 n 之间的序号 i，$a[i-k],a[i-k+1],\dots ,a[i+k]$ 这 2k+1 个数中的最小值是多少？

当某个下标超过 1 到 n 的范围时，数不存在，求最小值时只取存在的那些值。

输入格式

输入的第一行包含一整数 n。

第二行包含 n 个整数，分别表示 a[1], a[2], …, a[n]。

第三行包含一个整数 k 。

输出格式

输出一行，包含 n 个整数，分别表示对于每个序号求得的最小值。

样例输入

5
5 2 7 4 3
1

样例输出

2 2 2 3 3

评测用例规模与约定

对于 30%的评测用例，$1<n<=1000,1<=a[i]<=1000$。

对于60%的评测用例，$1<=n<=10000,1<=a[i]<=50000$。

对于所有评测用例，$1<=n<=100000,1<=a[i]<=1000000$。

🧠思路

这道题属于一个模板题，就是需要知道这个ST表的模板，接下来我来介绍一下

RMQ问题

RMQ（Range Minimum/Maximum Query），即区间最值查询，是指这样一个问题：对于一个长度N的数组，在多次询问中，每次都以O(1)的时间得到区间[a, b]的最大值或最小值。

ST ( Sparse Table ) 算法

ST（Sparse Table）算法是一个非常有名的在线处理RMQ问题的算法，它可以在$O(nlogn)$时间内进行预处理，然后在$O(1)$时间内回答每个查询。其思想就是保存以i为起点的某段数据的最小值。

预处理，用动态规划（DP）解决。思想接近于二路归并排序过程的分治思想。

1. 既然是DP思想，首先要记录每步的状态。

   设$A[i]$是要求区间最值的数列，$F[i,j]$表示从第$i$个数起连续$2^j$个数中的最大值。 这里的$F[i,j]$就是每步的状态。

例如：

A数列为：3 2 4 5 6 8 1 2 9 7

F[1，0]表示第1个数起，长度为2^0=1的最大值，其实就是3这个数。

同理 : F[1,1] = max(3,2) = 3, F[1，2]=max(3,2,4,5) = 5，F[1，3] = max(3,2,4,5,6,8,1,2) = 8;

2. 状态转移方程

   既然有每步的状态了，开始找状态转移方程。
   $$F[i,j]=max(F[i,j-1],F[i+2^{(j-1)}][j-1])$$

怎么理解呢？

最初始状态：F[0, 0] = A[0]; F[1,0] = A[1]; F[2,0] = A[2]; 意思是说每单个元素的最大值都是自己（因为只有一个元素）

下一个状态：F[0, 1] = max(F[0,0], F[1,0]) = max(A[0], A[1]);

意思是说把F[0, 1] 分成两段，例如要求得F[3, 2] = max(A[3] , A[4], A[5], A[6]) 其实就是求四个元素的前两个以及后两个的最大值。在求F[3,2]的时候已经知道了F[3, 1]和F[5,1]了。

我们可以在看一个图

显然，区间$[i,i+2^{j-1}-1]$和$[i+2^{j-1},i+2^j-1]$一定覆盖了区间$[i,i+2^j-1]$，从图中也可以看出区间$[i,i+2^j-1]$内的最大值就是区间$[i,i+2^{j-1}-1]$和$[i+2^{j-1},i+2^j-1]$内的最大值中更大的一个，所以就得到了上述的递推公式。
$$F[i,j]=max(F[i][j-1],F[i+2^{(j-1)}][j-1])$$
代码如下：

def RMQ():
    t=int(math.log2(length)) # 注意边界，取log2
    dp=[[0]*(t+1) for _ in range(length+1)]
    for i in range(1,length+1): dp[i][0]=data[i] # 初始化
    for j in range(1,t+1):
        for i in range(length-(1<<i)+1): # i + 1<<j - 1 <= n 进行转化
            dp[i][j]=max(dp[i][j-1],dp[i+(1<<(j-1))][j-1]) # 状态转移方程

查询区间

那么查询怎么做呢？毕竟我们存放的都是2次幂个数的最小值。假如查询的区间是奇数个，或不是2次幂个数怎么弄？

其实很简单，就是把头尾分开！

假如我们需要查询的区间为$(i,j)$，那么我们需要找到小于这个闭区间(左边界取i，右边界取j)的最大幂（可以重复，比如查询5，6，7，8，9，我们可以查询5678和6789)

1. 区间的长度为j - i + 1
2. 可以取t=log2( j - i + 1) 区间是1->3 就取 log2( 3 - 1 + 1) = 1小于等于区间的最大幂
3. RMQ(A, i, j)=max{F[i , t], F[ j - 2 ^ t + 1, t]}

所以总结下来，先计算出一个满足$2^t<r-l+1<2^{t+1}$的t值，即小于区间长度的2的最高次幂。

显然，区间$[l,l+2^{t-1}]$和$[r-2^t+1,r]$一定覆盖了区间[l,r]，如下图：

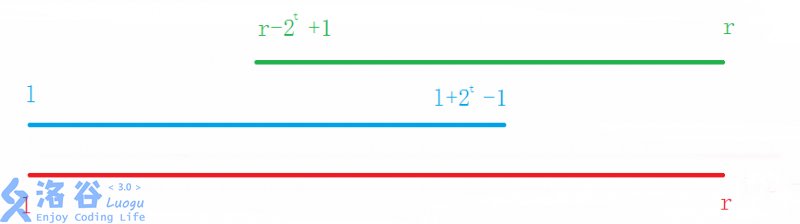
F[i, t] 是左边界起点向左找，F[ j - 2 ^ k + 1, k]是右边界作为终点，向右找起点。 一定要用小于等于区间的最大幂是因为要能够两个F加在一起能够覆盖整个区间。

所以知道了所有的方法，直接套用st模板即可

其实还有更简单的，但是可能不能全过，但是我们肯定能拿分，就是直接穷举呗，本身python也有min函数

🖥︎参考代码

ST模板

import math

# ST模板
class ST:
    def __init__(self,data):
        length = len(data)
        data = [0] + data # 变成 1-indexing
        t = int(math.log2(length)) # 取log2
        dp=[[float('inf')]*(t+1) for _ in range(length+1)] # 定义DP数组
        
        for i in range(1,length+1):
            dp[i][0] = data[i] # 初始化
        
        for j in range(1,t+1):
            for i in range(length-(1<<j)+1 + 1): # i + 1<<j - 1 <= n 进行转化
                dp[i][j]=min(dp[i][j-1],dp[i+(1<<(j-1))][j-1]) # 状态转移方程
            
        self.dp=dp
        
    def query(self,L,R):
        t = int(math.log2(R-L+1))
        dp= self.dp
        return min(dp[L][t],dp[R-(1<<t)+1][t])
    
n = int(input())
a = list(map(int,input().split())) # 0-indexing
k = int(input())
st = ST(a) # 构建st表
for i in range(1,n+1):
    l = max(1,i-k)  
    r = min(n,i+k)
    print(st.query(l,r),end=' ')

穷举

我感觉穷举可以拿60%的分

n = int(input())
a = list(map(int,input().split()))
k = int(input())

for i in range(n):
    l = max(0,i-k)
    r = min(i+k,n-1)
    print(min(a[l:r+1]),end=' ')