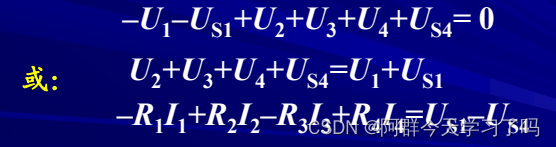电路中的电压、电流之间具有两种约束，一种是由电路元件决定的元件约束；另一种是元件间连接而引入的几何约束（就是拓扑约束），后者由基尔霍夫定律来表达。基尔霍夫定律是集总参数电路的基本定律。

电源又称为激励源或激励，由激励在电路中产生的电流、电压称为响应。有时，根据激励与响应之间的因果关系，把激励称为输入，响应称为输出。
电路理论研究电路中发生的电磁现象，并用电流、电压、电荷、磁通等物理量来描述其中的过程。
电路模型：反映实际电路部件的主要电磁性质的理想电路元件及其组合。
五种基本的理想电阻元件：

• 电阻元件：表示消耗电能的元件；
• 电感元件：表示产生磁场，储存磁场能量的元件；
• 电容元件：表示产生电场，储存电场能量的元件；
• 电压源和电流源：表示将其它形式的能量转变成电能的元件。

规定正电荷的运动方向为电流的实际方向，电位降低的方向为电压的实际方向。
导线上标示的箭头是电流的参考方向，它不一定就是电流的实际方向。
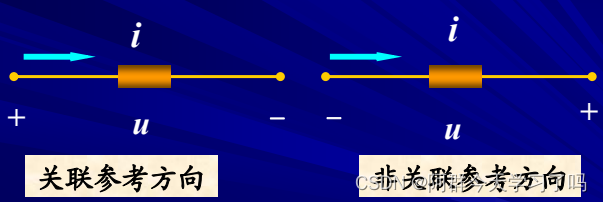
元件或支路的u，i 采用相同的参考方向称之为关联参考方向。反之，称为非关联参考方向。

电功率：单位时间内电场力所做的功。

• u, i 取关联参考方向时，P=ui。P>0 吸收功率，P<0 发出功率。
• u, i 取非关联参考方向时，P=-ui。P<0 吸收功率，P>0发出功率
  对一完整的电路，发出的功率=吸收的功率。

电路元件：电路中最基本的组成单元。

每种元件通过端子的两种物理量反映一种确定的电磁性质。
集总参数元件是指有关电、磁场物理现象都是由元件来“集总”表征，在元件外部不存在任何电场和磁场。由集总元件构成的电路称为集总参数电路。集总条件：d<<λ。


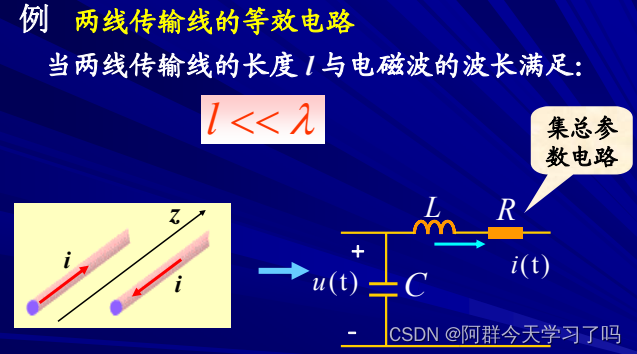
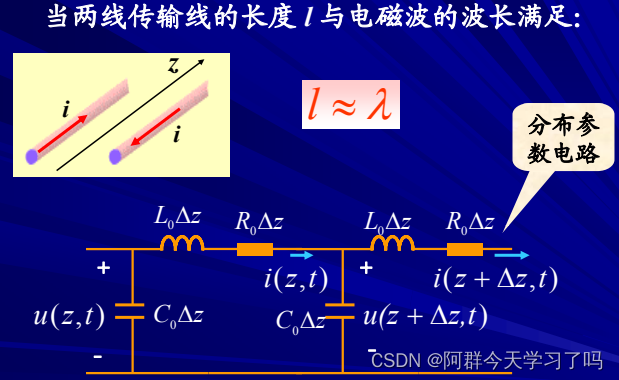
情况不同，抽象出来的电路模型就不一样。

电阻元件：对电流呈现阻力的元件。其特性可用u~i平面上的一条曲线（伏安特性曲线）来描述。

关于欧姆定律：

• 只适用于线性电阻；
• 如电阻上的电压与电流参考方向非关联，公式中应冠以负号；
• 说明线性电阻是无记忆、双向性的元件。
  电阻元件在任何时刻总是消耗功率的。

常用的是理想电压源和理想电流源。

实际电流源的产生：可由稳流电子设备产生，如晶体管的集电极电流与负载无关；光电池在一定光照下光电子被激发产生一定值的电流等。
实际电源：

• 干电池和纽扣电池（化学电源）；
• 燃烧电池（化学电源）；
• 太阳能电池（光能电源）；
• 蓄电池（化学电源）；

受控源：电压或电流的大小进而方向不是给定的时间函数，而是受电路中某个地方的电压（或电流）控制的电源。（包括四种）
受控源反映的是电路中某处的电压或电流对另一处的电压或电流的控制关系，在电路中不能作为“激励”。

基尔霍夫定律包括基尔霍夫电流定律 （KCL）和基尔霍夫电压定律( KVL)，反映了电路中所有支路电压和电流所遵循的基本规律，是分析集总参数电路的基本定律。

基尔霍夫电流定律 （KCL）：在集总参数电路中，任意时刻，对任意结点流出（或流入）该结点电流的代数和等于零。
举个例子：

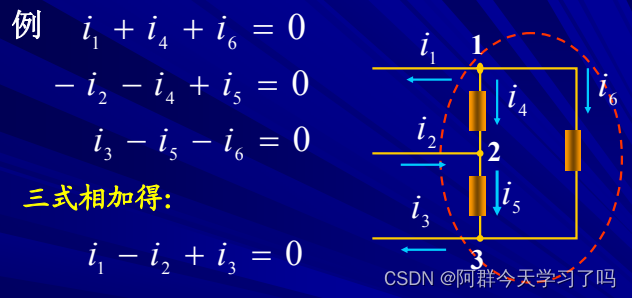
注意：

• KCL是电荷守恒和电流连续性原理在电路中任意结点处的反映；
• KCL是对结点处支路电流加的约束，与支路上接的是什么元件无关，与电路是线性还是非线性无关；
• KCL方程是按电流参考方向列写的，与电流实际方向无关。

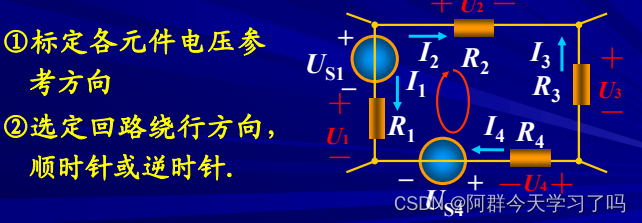
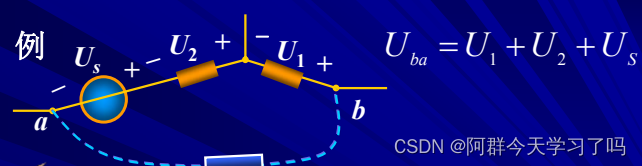
基尔霍夫电压定律（KVL）：在集总参数电路中，任一时刻，沿任一回路，所有支路电压的代数和恒等于零。
举例子：