当我们遇到了要快速判断一个元素是否出现集合里的时候,就要考虑哈希法。哈希法是牺牲了空间换取了时间,要使用额外的数组,set或者是map来存放数据,才能实现快速的查找。

当我们要使用集合来解决哈希问题的时候,优先使用unordered_set,因为它的查询和增删效率是最优的,如果需要集合是有序的,那么就用set,如果要求不仅有序还要有重复数据的话,那么就multiset。
而map 是一个key value 的数据结构,map中,对key是有限制,对value没有限制的。
242、有效的字母异位词
242、有效的字母异位词
介绍
给定两个字符串 s 和 t ,编写一个函数来判断 t 是否是 s 的字母异位词。注意:若 s 和 t 中每个字符出现的次数都相同,则称 s 和 t 互为字母异位词。

思路
暴力思路:两层for循环,一层for循环遍历字符串,另一个for循环遍历另一个字符串,看第一个for循环中的字符有没有出现过。
哈希法:数组(范围可控)、set(范围很大)、map(key--value)
本题中a-z中ASCII码是连续的。a可以对应到数组下标位0的位置,z可以对应到数据下表为25的位置。因此,可以定义一个数组hash[26];
用该数组统计第一个字符串里每个字符出现的频率。然后第二个字符串每个字符出现的频率在数组的基础上做减法。如果最后数组hash中的所有元素都为0,那么就是有效字母异位词。

//定义哈希数组,默认该数组中的值为0
int hash[26];
for(i=0;i<s.size;i++){
hash[s[i]-'a']++;
}
for(i=0;i<t.size;i++){
hash[t[i]-'a']--;
}
for(i=0;i<26;i++){
if(hash[i]!=0)
return false;
}
return true;代码
class Solution {
public:
bool isAnagram(string s, string t) {
int hash[26] = {0};
for(int i=0;i<s.size();i++){
hash[s[i]-'a']++;
}
for(int i=0;i<t.size();i++){
hash[t[i]-'a']--;
}
for(int i=0;i<26;i++){
if(hash[i]!=0)
return false;
}
return true;
}
};349、两个数组的交集
349、两个数组的交集
介绍
给定两个数组 nums1 和 nums2 ,返回 它们的交集 。输出结果中的每个元素一定是 唯一 的。我们可以 不考虑输出结果的顺序 。

思路一 数值很大使用set
若数值很大,可以使用set来做哈希映射。若数值很大,但是分布很分散,也可以用set。
将nums1数组放到哈希表里,然后遍历nums2的元素,查看每个元素是否在哈希表中出现,若出现,则放到新数组中,并且最后要去重。
set在C++中:
set
unordered_set(无限存装的数组) 做映射和取值操作时效率最高
multi_set
unordered_set result (unordered_set会自动做去重)
unordered_set number_set(nums1) //直接把nums1数组转变为unordered_set存储结构
//使用num2在number_set中做遍历查询操作
for(i=0;i<nums2.size'i++){
if(number_set.find(nums2[i]) != nums_set.end()) //如果找到了该元素
result.inset(nums2[i])
}
return vector(result...)思路二 数值较小使用数组
定义一个1005的数组
unordered_set result;
int hash[1005]={0}
//把nums1处理成哈希表结构
for(i=0;i<nums1.size;i++){
hash[nums1[i]] =1;
}
//遍历nums2
for(i=0;i<nums2.size;i++){
if(hash[nums2[i]] == 1)
result.insert(nums2[i])
}代码
class Solution {
public:
vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
unordered_set<int> result;//unordered_set会自动去重
unordered_set<int> nums_set(nums1.begin(),nums1.end());
for(int i=0;i<nums2.size();i++){
//find方法如果没找到该元素在哈希表中,则会返回end
if(nums_set.find(nums2[i])!=nums_set.end())
result.insert(nums2[i]);
}
return vector<int>(result.begin(),result.end());
}
};class Solution {
public:
vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
unordered_set<int> result;//unordered_set会自动去重
int hash[1005] = {0};
//把nums1处理成哈希表结构
for(int i=0;i<nums1.size();i++){
hash[nums1[i]] = 1;
}
//遍历nums2
for(int i=0;i<nums2.size();i++){
if(hash[nums2[i]]==1)
result.insert(nums2[i]);
}
return vector<int>(result.begin(),result.end());
}
};202、快乐数
202、快乐数
介绍


思路
如何求一个数中每一位的平方和。
明确无限循环的概念,即如果新的平方和在之前的计算中出现过(因此可以想到使用哈希表),那么这就算一个无限循环。
代码
class Solution {
public:
int getSum(int n){
int sum = 0;
while(n){
sum = sum + (n%10)*(n%10);
n = n/10;
}
return sum;
}
bool isHappy(int n) {
unordered_set<int> set;//定义存储每次的平方和
while(1){
int sum = getSum(n);
if(sum == 1)
return true;
// 如果这个sum在set中出现过,那么就说明陷入无限循环,要立即跳出
if(set.find(sum)!=set.end()){
return false;
}else{
set.insert(sum);
}
n = sum;
}
}
};1、两数之和
1、两数之和
介绍
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案。但是,数组中同一个元素在答案里不能重复出现。
你可以按任意顺序返回答案。


思路
每当遇到要判断这个元素是否出现过的第一反应就应该是哈希法。
例如:如果遍历到3,就应该判断前面是否遍历过6。
如何判断是否遍历过?将遍历过的元素加入到一个集合里。每次遍历新元素x的时候,在这个集合里判断9-x是否出现过。
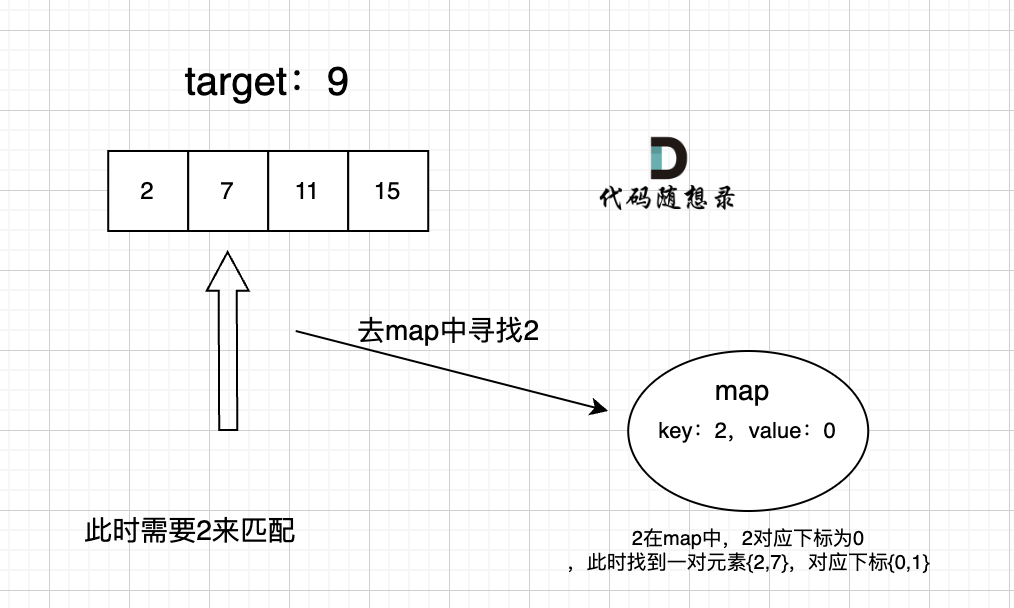
集合---采用一种哈希表的结构--由于不仅要找一个元素,还要知道这个元素在原数组中的下标,所以应该选用map结构。

map的key和value---思考我们查找的是什么,我们查找的是一个元素是否出现过,那么就应该将元素作为map中的key。(map能以很快的速度查找key【这里的元素】是否在map中出现过)
map在该题中是存放我们遍历过的元素。
//map--unordered_map(存和读效率最高)--multi_map
//首先定义一个map,要定义该map的key和value,用于存放遍历过的元素
unordered_map(int,int) map;
for(i=0;i<nums.size;i++){
//查询每个元素是否在map中
s = target - nums[i] //要查询的key
iter = map.find(s);
if(iter!=map.end()) //如果要查询的key在map中出现过
return {iter->value,i};
map.insert(nums[i],i);//把遍历过的元素加入到map中
}
return {};代码
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
std::unordered_map<int,int> map;
for(int i=0;i<nums.size();i++){
//查询每个元素是否在map中
int s = target - nums[i];
auto iter = map.find(s);
if(iter!=map.end())
return {iter->second,i};
map.insert(pair<int,int>(nums[i],i));
}
return {};
}
};