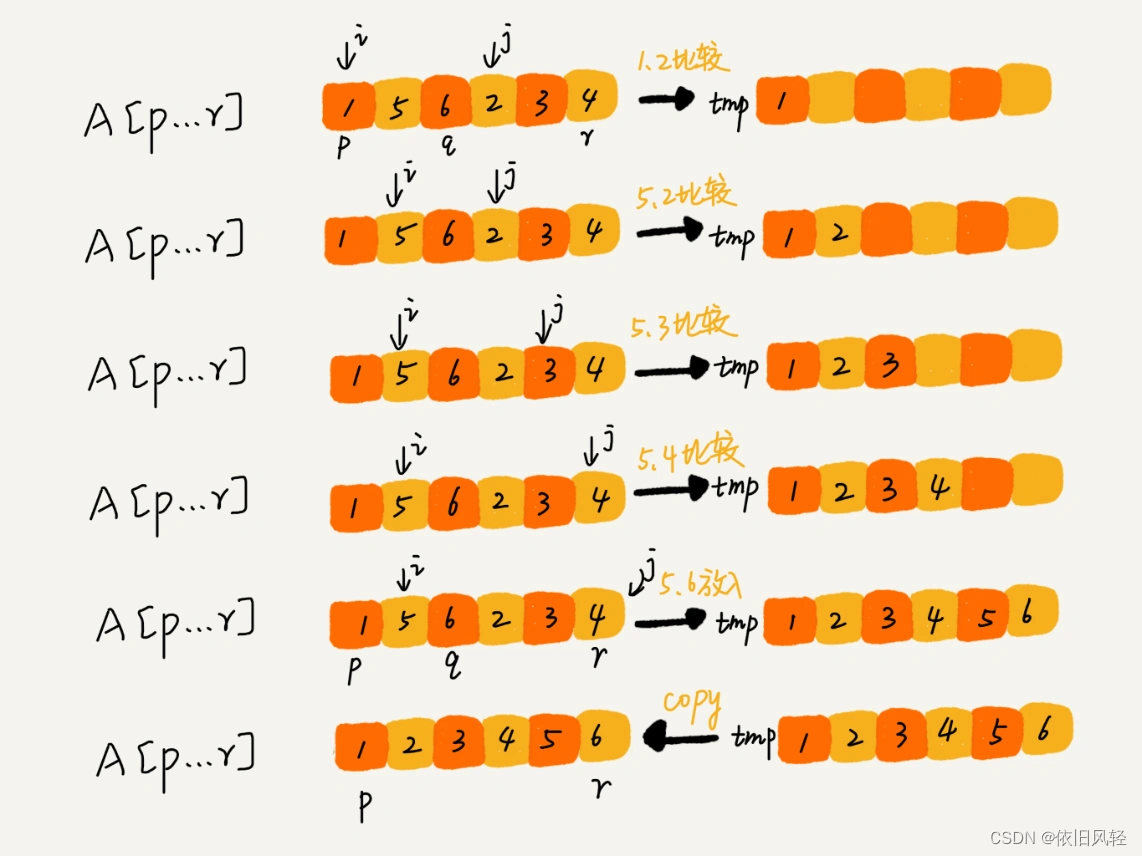作者:学Java的冬瓜
博客主页:☀冬瓜的主页🌙
专栏:【C/C++数据结构与算法】
分享:本王在此,狼狈为奸者,谋权篡位者,倒行逆施者,都得死! ——岐王李茂贞《画江湖之不良人》
主要内容:八大排序选择排序中的归并排序(递归+非递归)、计数排序。以及对排序的总结和稳定性的判断。


文章目录
- 一、归并排序
- 1. 思路
- 2. 复杂度
- 3. 代码
- 4. 补充:归并非递归写法
- 二、计数排序(非比较排序)
- 1. 代码
- 2. 理解
- 三、基数排序(桶排序)
- 思路
- 四、排序总结
- 1. 内部排序
- 2. 稳定性
一、归并排序
1. 思路
- 利用一个长度为n的数组,利用
分治的原理,每次分两个区间,去递归;递归返回后就是左右两个区间已经有序。就把左右两个区间的数归并到新开的数组tmp中;最后再把tmp中的数拷贝回a数组。
例子:
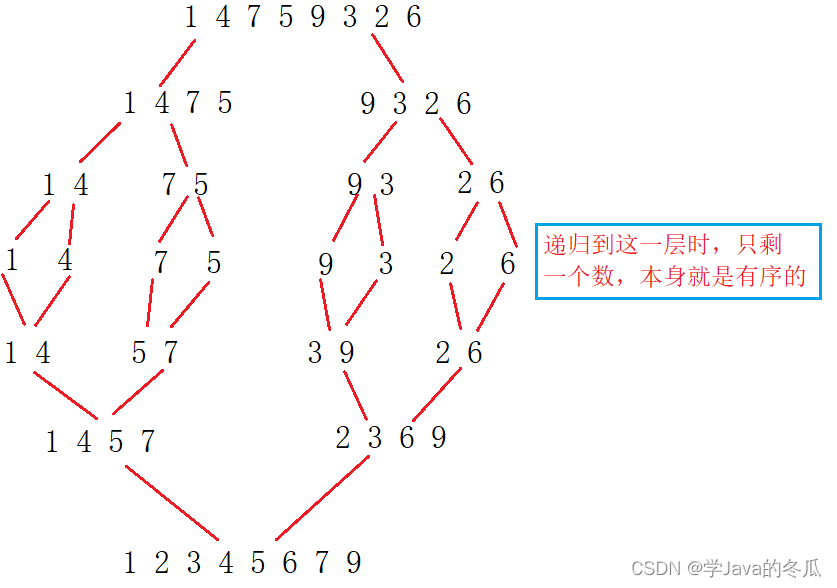
2. 复杂度
- 时间复杂度:
O(NlogN),(非递归的时间复杂度也是O(NlogN))。每次分两组区间去递归,然后再合起来归并,共n个数,所以需要logn趟。每一趟需要遍历一遍,所以为O(NlogN)。 - 空间复杂度:
O(N),归并排序利用了长度为n的tmp数组,作为辅助空间。
3. 代码
// 归并排序
void _MergeSort(int* a, int left, int right, int* tmp)
{
if (left >= right) { //表示递归到只有一个数了,就已经有序
return;
}
// 1.递归,去让左右子区间有序
int mid = (left + right) / 2;
_MergeSort(a, left, mid, tmp);
_MergeSort(a, mid + 1, right, tmp);
// 2.左右区间有序,开始归并(将两组数归并到tmp数组中)
int begin1 = left, end1 = mid;
int begin2 = mid + 1, end2 = right;
int index = left;
while (begin1 <= end1 && begin2 <= end2) {
if (a[begin1] <= a[begin2]) { // 这里是"<=",就是稳定的排序
tmp[index++] = a[begin1++];
}
else {
tmp[index++] = a[begin2++];
}
}
while (begin1 <= end1) {
tmp[index++] = a[begin1++];
}
while (begin2 <= end2) {
tmp[index++] = a[begin2++];
}
// 3.拷贝回a数组
for (int i = left; i <= right; i++) {
a[i] = tmp[i];
}
}
void MergeSort(int* a, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
_MergeSort(a, 0, n - 1, tmp);
free(tmp);
}
4. 补充:归并非递归写法
代码如下:
// 归并排序
void MergeSortNonR(int* a, int n)
{
int* temp = (int*)malloc(sizeof(int) * n);
int gap = 1;
while (gap < n) {
int index = 0; // 这个控制temp数组下标的变量,在for循环之外,否则永远是归并结果永远放在前一组
for (int i = 0; i < n; i += 2 * gap) {
// 【i,i+gap-1】【i+gap,i+2*gap-1】 这两组数归并,gap=1时,11归2;gap=2时,22归4;gap=4时,44归8
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
// 1. 左半区间不完整,或者右半区间没有数据了,比如10个数,11归2,最后一组没有右半区间。
if (begin2 >= n) {
break;
}
// 2. 当11个数,22归4时,最后一组右半区间不完整,需要修正再去归并,最后一组变成21归并。(可见例子)
if (end2 >= n) {
end2 = n - 1;
}
// 归并代码
while (begin1 <= end1 && begin2 <= end2) {
if (a[begin1] < a[begin2]) {
temp[index++] = a[begin1++];
}
else {
temp[index++] = a[begin2++];
}
}
while (begin1 <= end1) {
temp[index++] = a[begin1++];
}
while (begin2 <= end2) {
temp[index++] = a[begin2++];
}
// 注意:把范围内的temp数组拷贝回a数组
for (int j = i; j <= end2; j++) { // end2是已经修正过的
a[j] = temp[j];
}
}
gap *= 2;
}
free(temp);
}
- 如何理解归并非递归算法:

现在,我们来了解几个可能会出错的地方:
-
index = 0 要放在for循环之外,这个控制temp数组下标的变量,在for循环之外,否则index不会按顺序给temp数组归并赋值。
-
把temp拷贝到a数组,不能gap一趟完成后再拷贝(不能把temp拷贝回a数组放在for循环之外),而且要适当操作才不会数组越界,否则会出现以下问题:

-
怎么解决越界问题?

-
怎么解决,产生随机数的问题?

- 小结:怎么实现递归转非递归? 有两种思路:
1> 循环 2>利用数据结构的栈或者队列。 - 那为什么快排用栈实现,而归并用循环实现呢?
因为快排的形式和二叉树遍历的思路很像,利用栈可以轻松实现。而这里的归并,越界时边界end2的修正以及,直接break都需要控制边界,即使利用栈或队列也是需要控制边界的,而且使用栈或者队列还会有额外的空间开销。 - 此外,归并排序又叫外排序,也就是说:
归并排序处理可以内部排序(在主存中),它还可以外部排序(在磁盘上)。
举个例子:有一个8G的文件需要排序,而内存(也可称主存)只有1G的空间,该怎么实现排序?
方法:首先,把8G内存切割成8个1G的文件,分别再把每个1G的文件读入到内存中,各自用快速排序,排序后每个1G的文件有序。此时内存只有1G,我们要继续让这八个1G的文件有序,可以知道,要想继续在内存中排序是不行了。这时,就用到了外部排序。就是把两个1G的文件在磁盘上进行归并排序(11归2),把归并结果写入另一个文件中(这一组11归2归并完后,这文件大小就是2G),然后重复操作22归4,44归8,不是2的倍数个文件,需要控制好边界。其实就和内部排序归并的思想一样,只是操作对象是文件而不是简单的数了。
二、计数排序(非比较排序)
1. 代码
// 计数排序
void CountSort(int* a, int n)
{
int max = a[0], min = a[0];
for (int i = 1; i < n; i++) {
if (max < a[i]) {
max = a[i];
}
if (min > a[i]) {
min = a[i];
}
}
int range = max - min + 1;
int* count = (int*)malloc(sizeof(int) * range); // 11 12 10 15 17 17
memset(count, 0, sizeof(int) * range); // count是计算a[i]出现次数的,所以初始化为0
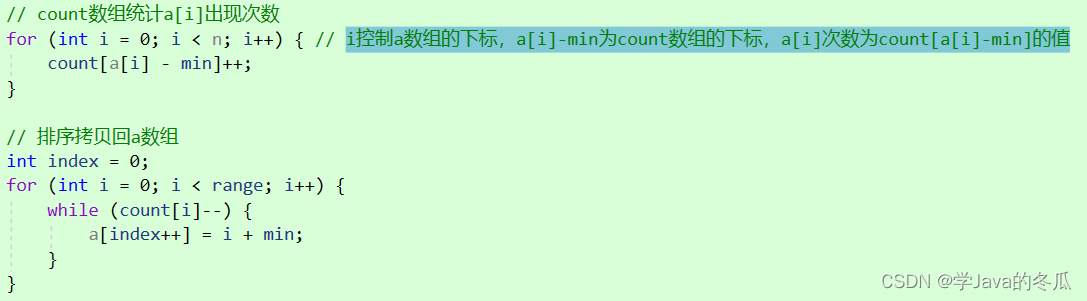
// count数组统计a[i]出现次数
for (int i = 0; i < n; i++) { // i控制a数组的下标,a[i]-min为count数组的下标,a[i]次数为count[a[i]-min]的值
count[a[i] - min]++;
}
// 排序拷贝回a数组
int index = 0;
for (int i = 0; i < range; i++) {
while (count[i]--) {
a[index++] = i + min;
}
}
}
2. 理解
- 思路:先统计,再按照统计范围,拷贝回原数组,利用映射(和哈希函数很相似)。
- 第一部分:
i控制a数组的下标,a[i]-min为count数组的下标,a[i]次数为count[a[i]-min]的值,举个例子:12 16 10 15 18 18 15计数排序。计算出max=18,min=10 => range=9。统计a中值的次数时,count[a[0]-10]++ => count[2]++,2是12的映射,其它统计同理。所以可以推出a[i]-min是a[i]的映射。 - 第二部分:把count数组大于1的值(count(i)表示i+min在a数组中出现的次数),映射回a数组。
i代表count的下标,index代表a的下标,i+min是a[index]的映射 - 那么为什么要用映射?最根本的原因就是为了节省空间。因为如果是10001, 10002 ,10001, 10008这种集中但是较大的数,如果不用映射,count数组前10000个空间都用不到,造成空间大量浪费。
- 时间复杂度:
O(N + range)。 - 在上面的思考中我们也可以发现,
计数排序适合范围较小,即比较集中的数,否则空间浪费较大
三、基数排序(桶排序)
思路
先按照一组数的个位排序,然后按照十位排序…,结果就是桶排序的结果。
四、排序总结
1. 内部排序
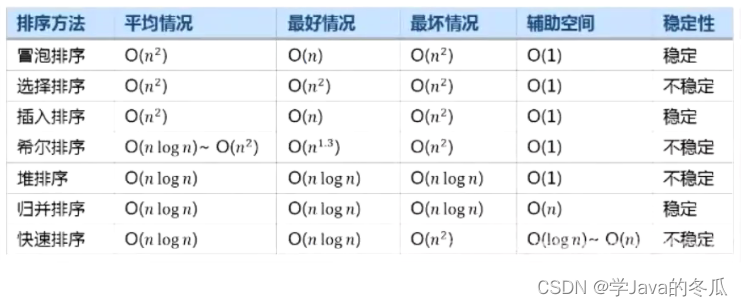
对于复杂度和代码以及排序的理解可以看该专题栏下其它博客:【数据结构与算法】
2. 稳定性
- 首先,稳定性的定义是:
排序前后,相同的值的数相对位置不变,比如说2 5 7 9 5在排序后,第二个5仍然在第5个5的前面。 - 接下来我们谈谈这些排序为什么稳定,为什么不稳定。
冒泡排序:可以在a[j] > a[j+1]才交换,即相等时不交换,人为控制稳定。
插入排序和冒泡排序和归并排序都一样,在比较时,可以控制稳定。 - 不稳定排序分析
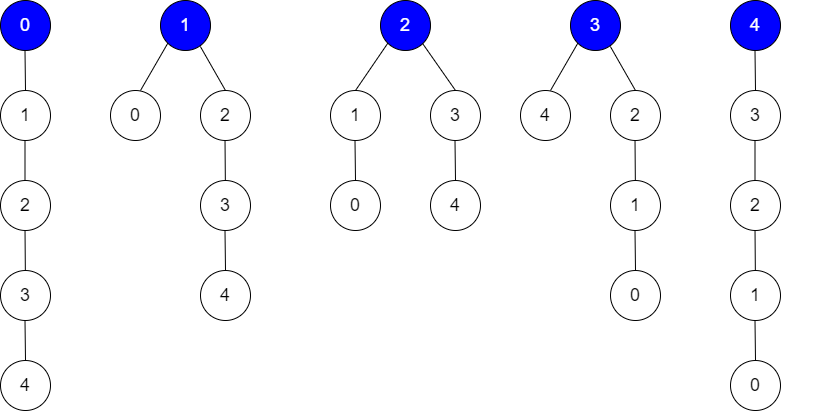
选择排序:5 7 5 8 2 6 5,找小,2和第一个5交换,那么第一个5和第二个5的相对位置就变了,即被动改变了相对位置。
希尔排序:在预排序时,分为多组数,这多组数里相同的值在自己组的位置不一样,比如这个相同的数是8,在排序前第一组中8在第一个位置,而第二组8在后面的位置,但是8是第一组数的最大值,第二组数的最小值,排序后,相对位置就会改变。
堆排序:大堆时,把根节点与n-1下标的数交换后,n-1下标的数和与n-1下标相等的数相对位置可能就会改变。
快速排序:4 2 6 8 2,比如挖坑法,4为key时,右边找小,右边第一个2移动到4的位置,那么和左边第二个2的相对位置改变。 - 那么稳定性的用处在哪里?举一个很简单的例子,比如上机考试,两个人的成绩一样,但是做题时间不同,那排名在前的一定是用时较短的那一个人。可以作为比较的另一个定性。



![Mysql全解[中级篇]](https://img-blog.csdnimg.cn/97b4fc2cb073488eacb7ef85bc3f398d.png)