致前行的人：    

        人生像攀登一座山，而找寻出路，却是一种学习的过程，我们应当在这过程中，学习稳定冷静，学习如何从慌乱中找到生机。

目录

1.注释符号：

2.续接符和转义符：

3.回车与换行：

4.单引号和双引号：

5.计算机为何存在字符：

6.逻辑运算符：

7.位运算符：

8.如何理解整型提升

9.左移和右移 

10++、--操作

10.1深刻理解 a++

10.2++，--使用时会存在的问题

11.符号

1.注释符号：

注：注释在预处理的时候本质上是被替换成空格 

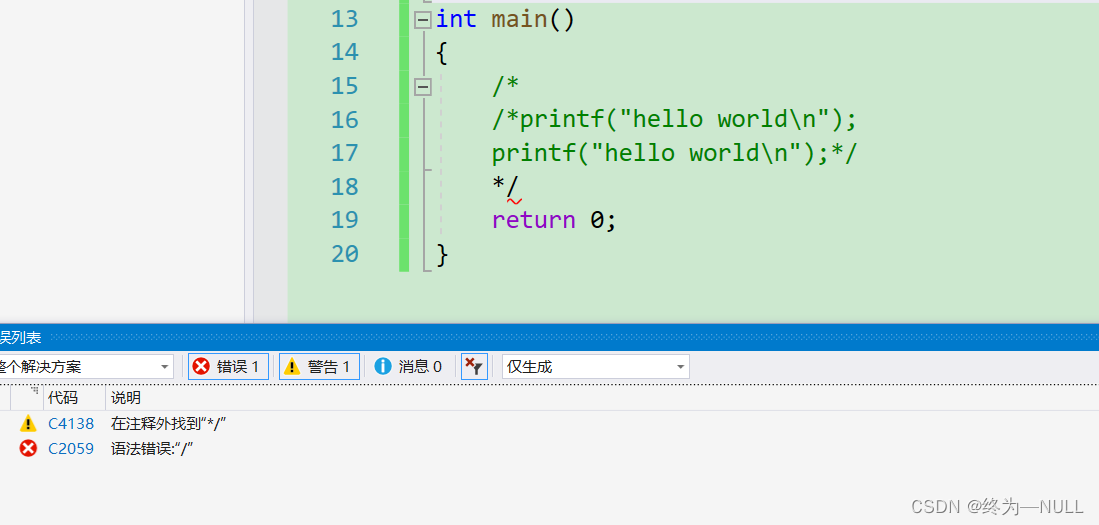
C分格的注释不支持嵌套：

 /*总是离它最近的*/匹配

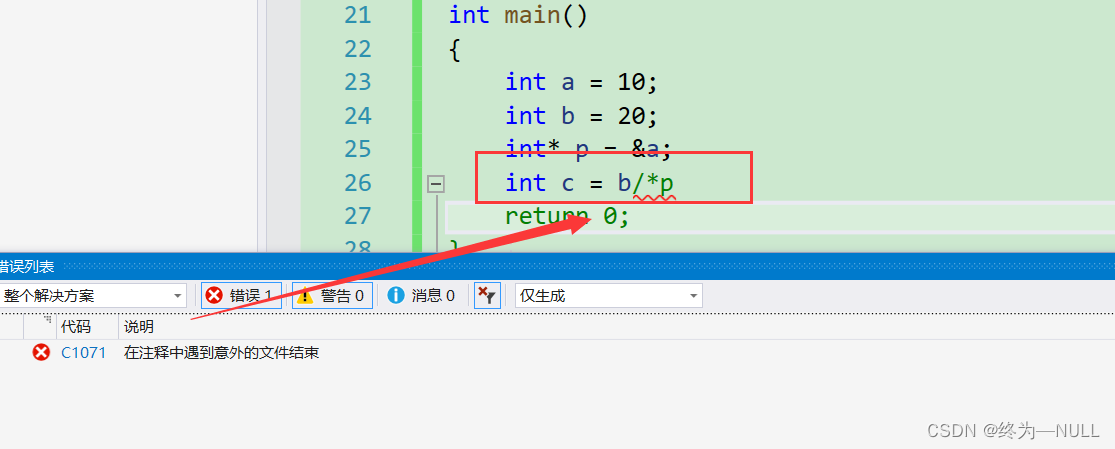
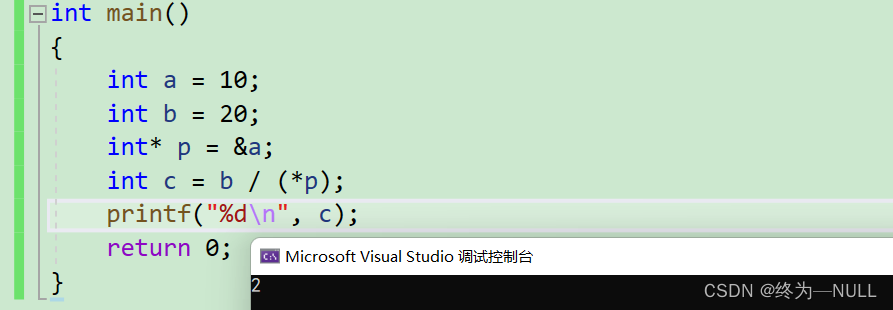
注释与指针：

 当/*在一起的时候编译器会默认为注释符号，为了避免应该加上（）：

2.续接符和转义符：

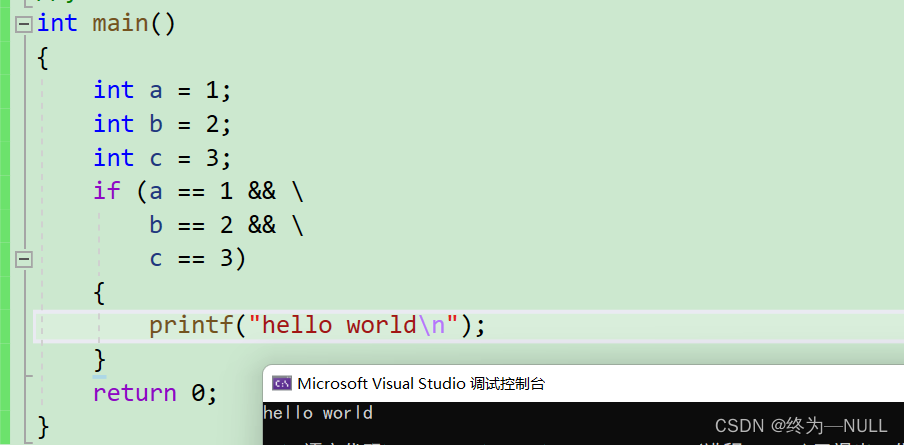
1.续行功能：

\:这里\充当续行的功能

注意：\的后面不能出现任何任何字符包括空格

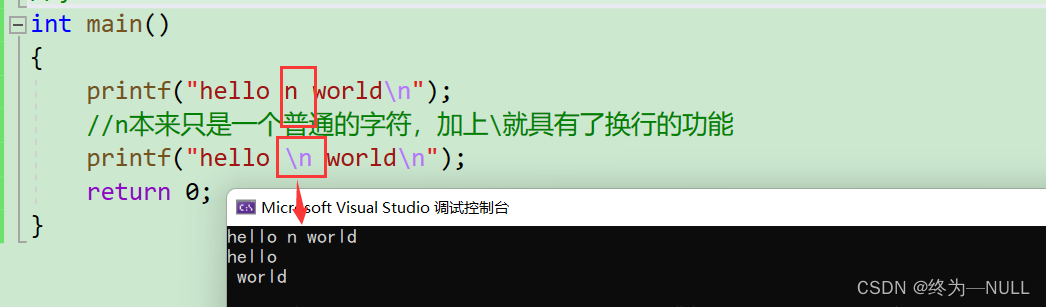
 2.转义功能：

1.字面转特殊：

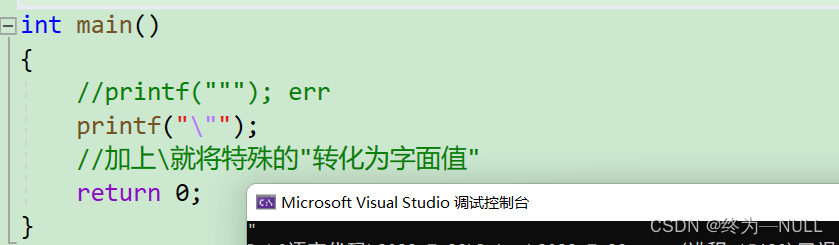
2.特殊转字面：

 

3.回车与换行：

回车：是将光标从当前的位置移动到开始位置   \n

换行：是移动到下一行                                       \r

验证：倒计时

4.单引号和双引号：

单引号是字符，双引号是字符串：

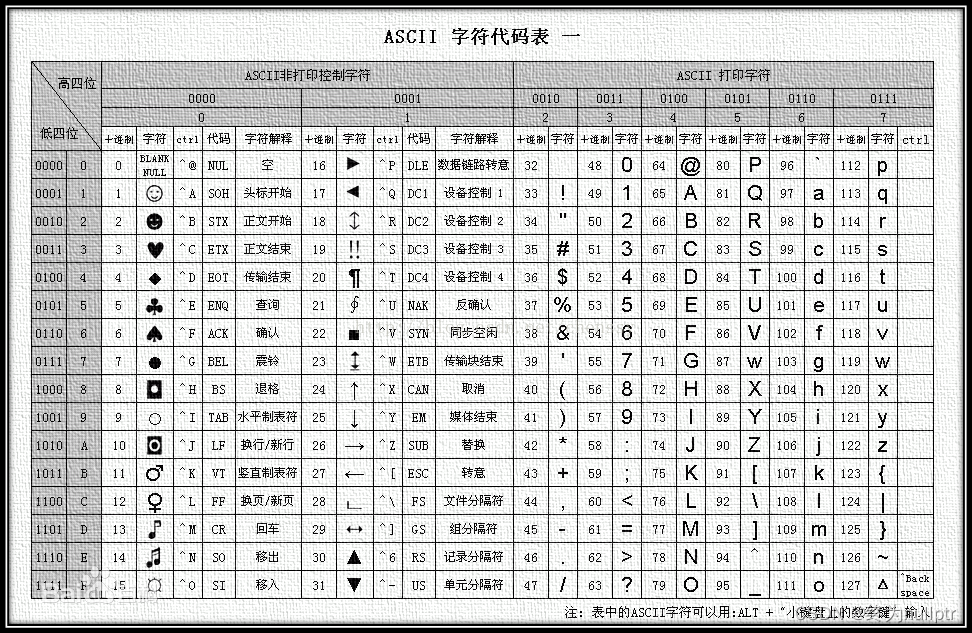
5.计算机为何存在字符：

为何会存在ASCCII表？
1.数据在内存中存储是以二进制的形式存储的，而为了让用户在显示器上清楚易懂的读取，则创造了不同的二进制对应不同的字符。

2.每一种字符又是英语是因为计算机最早是美国人发明的，而他们的语言又是英语，为了简单则用不同的英文字母来对应二进制数据

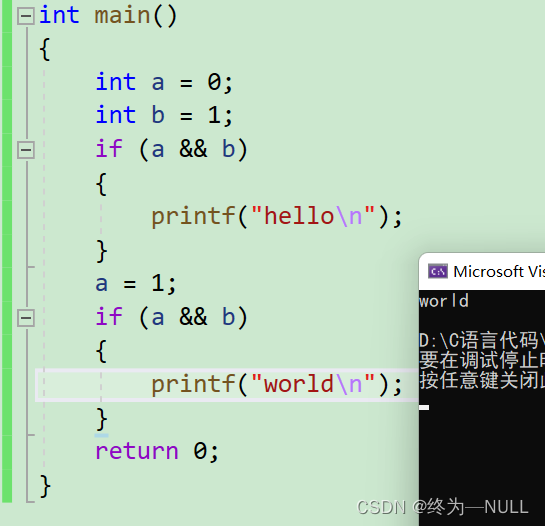
6.逻辑运算符：

&&：并且 两个条件为真则为真

||：或       有一个条件为真则为真

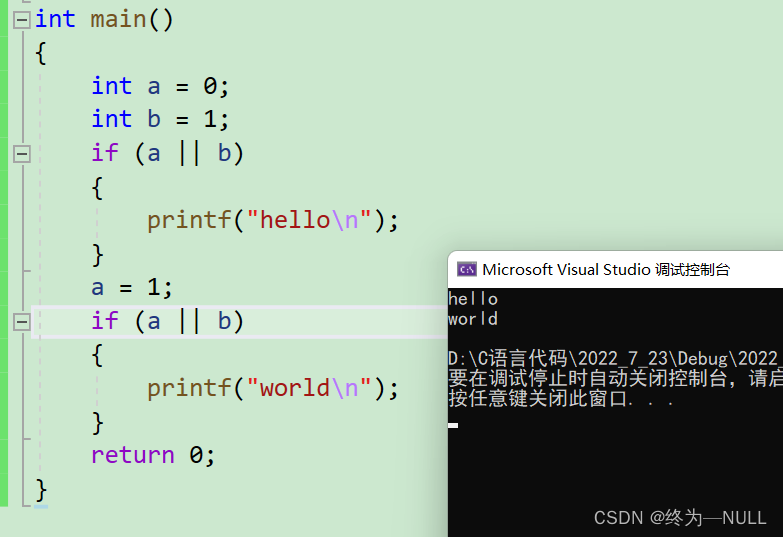
 短路：

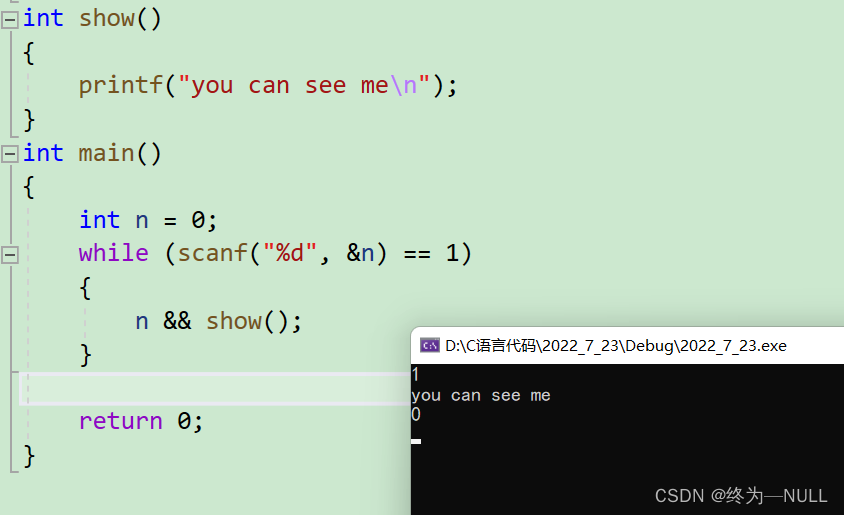
&&：当前面的条件为假时后面的表达式不进行

||：   当前面的条件为真时后面的表达式不执行

7.位运算符：

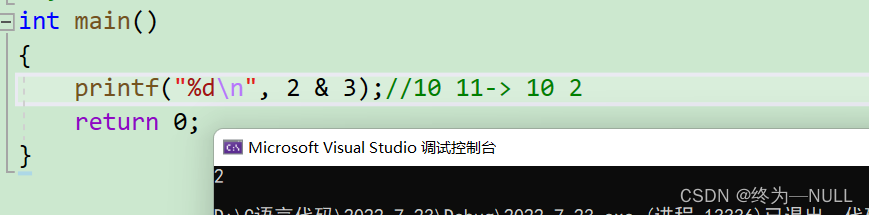
&：按位与 相同则为1，相异则为0

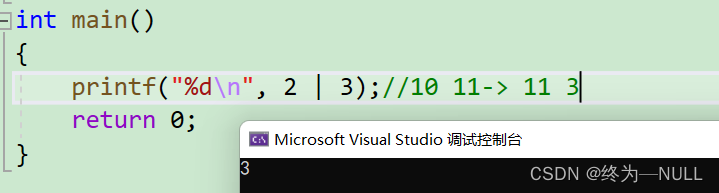
|：按位或  有一个为1则为1

^:按位异或 相异则为1，相同则为0

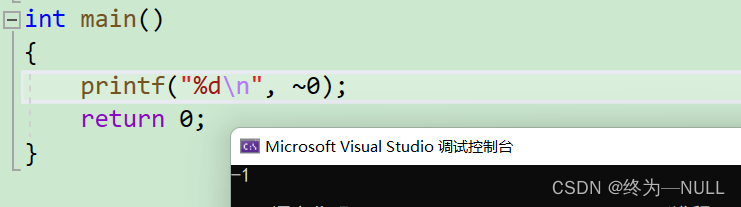
~：按位取反 

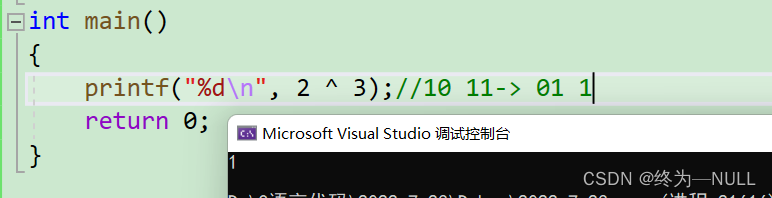
^的理解：

^:逐比特位，相同则为0，相异为1

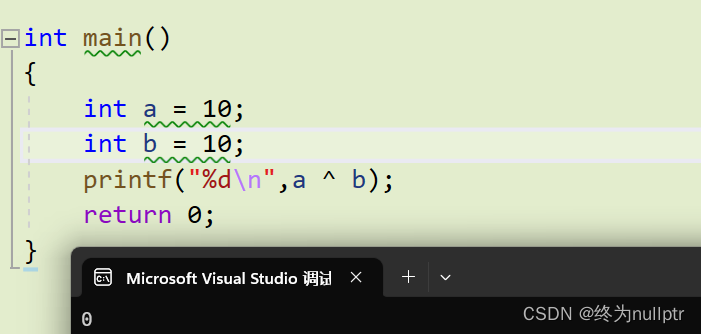
任何数和0异或，都是它本身 

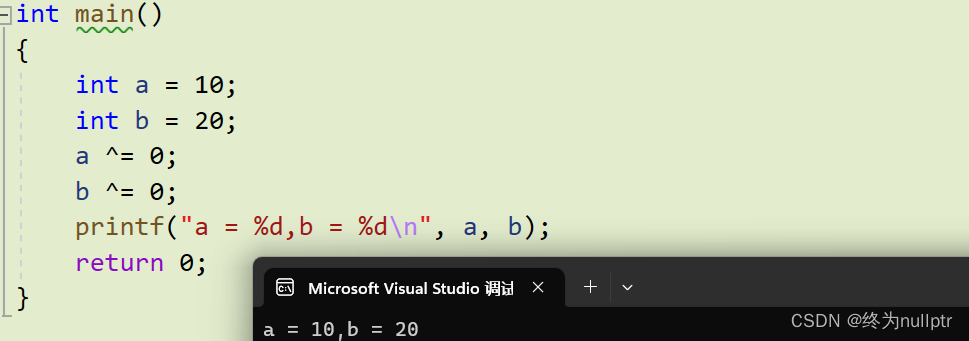
支持结合律和交换律 

 交换两个整数：

方法1：创建临时变量

void swap(int* p1, int* p2)
{
	int tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}
int main()
{
	printf("before:a = %d,b = %d\n", a, b);
	int a = 10;
	int b = 20;
	swap(&a, &b);
	printf("after:a = %d,b = %d\n", a, b);
	return 0;
}

方法2： 不创建临时变量

int main()
{
	int a = 10;
	int b = 20;
	printf("before:a = %d,b = %d\n", a, b);
	a = a + b;
	b = a - b;
	a = a - b;
	printf("after:a = %d,b = %d\n", a, b);
	return 0;
}

存在的问题：当a和b是两个非常大的数时，由于相加就可能会存在整型溢出的问题

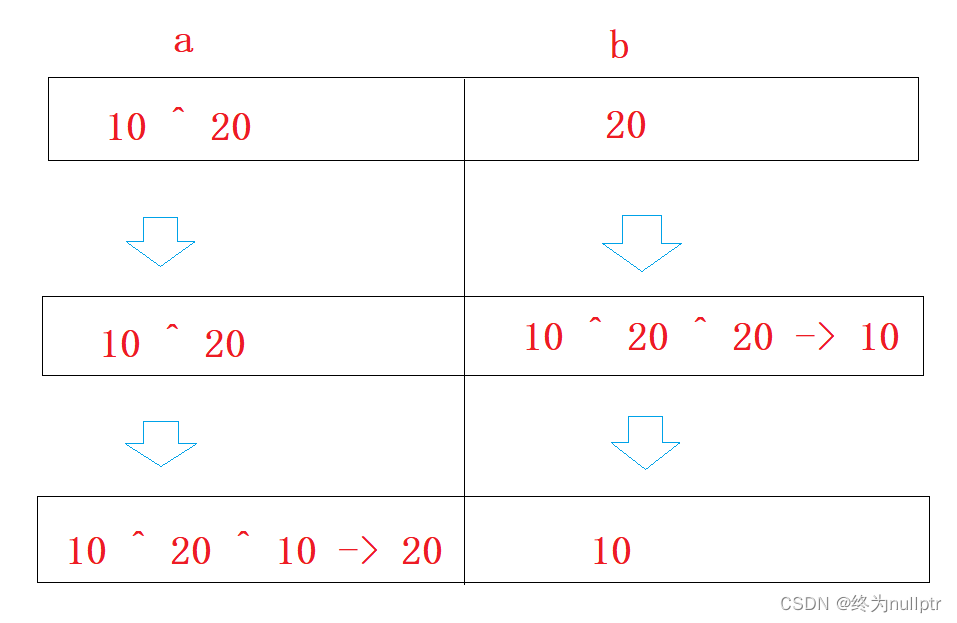
方法3：用异或解决整型溢出的问题

int main()
{
	int a = 10;
	int b = 20;
	printf("before:a = %d,b = %d\n", a, b);
	a = a ^ b;
	b = a ^ b;
	a = a ^ b;
	printf("after:a = %d,b = %d\n", a, b);
	return 0;
}

 图例解释：

将指定bit位置为1 ：

将指定bit位置为0：

#define SETBIT(x,n) (x |= (1 << (n - 1))) //将指定bit位置为1
#define CLRBIT(x,n) (x &= (~(1 << (n-1)))) //将指定bit位置为0
void show_bits(int x)
{
	int num = sizeof(x) * 8 - 1;
	while (num >= 0)
	{
		if (x & (1 << num))
			printf("1 ");
		else
			printf("0 ");
		num--;
	}
}
int main()
{
	int x = 10;
	SETBIT(x, 5);
	CLRBIT(x, 5);
	show_bits(x);
	return 0;
}

8.如何理解整型提升

无论任何位运算符，目标都是要计算机进行计算的，而计算机中只有CPU具有运算能力(先这样简单理解)，但计算的数据，都在内存中。故，计算之前(无论任何运算),都必须将数据从内存拿到CPU中，拿到CPU哪里呢？毫无疑问，在CPU 寄存器中。
而寄存器本身，随着计算机位数的不同，寄存器的位数也不同。一般，在32位下，寄存器的位数是32位。可是，你的char类型数据，只有8比特位。读到寄存器中，只能填补低8位，那么高24位呢？就需要进行“整形提升”。

#include<stdio.h>
int main()
{
	char c = 0;
	printf("sizeof(c): %d\n", sizeof(c)); 
	printf("sizeof(c): %d\n", sizeof(~c)); 
	printf("sizeof(c): %d\n", sizeof(c << 1)); 
	printf("sizeof(c): %d\n", sizeof(c >> 1));
	return 0;
}

9.左移和右移 

<<(左移): 最高位丢弃，最低位补零
>>(右移)：
1. 无符号数：最低位丢弃,最高位补零[逻辑右移]
2. 有符号数：最低位丢弃，最高位补符号位[算术右移]

int main()
{
	//左移
	unsigned int a = 1;
	printf("%u\n", a << 1);
	printf("%u\n", a << 2);
	printf("%u\n", a << 3);
	return 0;
}

int main()
{
	// 逻辑右移
	unsigned int b = 100;
	printf("%u\n", b >> 1);
	printf("%u\n", b >> 2);
	printf("%u\n", b >> 3);
	return 0;
}

 

int main()
{
	// 算术右移，最高位补符号位1，虽然移出了最低位1，但是补得还是1
	int c = -1;
	printf("%d\n", c >> 1);
	printf("%d\n", c >> 2);
	printf("%d\n", c >> 3);
	return 0;
}

 

int main()
{
	unsigned int d = -1;
	printf("%d\n", d >> 1);
	printf("%d\n", d >> 2);
	printf("%d\n", d >> 3);
	return 0;
}

 

结论：
左移，无脑补0
右移，先判定是算术右移还是逻辑右移，判定依据：看自身类型，和变量的内容无关。

10++、--操作

int main()
{
	int a = 10;
	int b = ++a; //前置++， 先自增在使用
	printf("%d, %d\n", a, b); //11,11
	int c = 10;
	int d = c++; //后置++，先使用在自增
	printf("%d, %d\n", c, d); //11,10
	//--同上
	return 0;
}

10.1深刻理解 a++

int main()
{
	int a = 10;
	int b = a++;

	int c = 20;
	c++;
	return 0;
}

结论：a++完整的含义是先使用，在自增。如果没有变量接收，那么直接自增

10.2++，--使用时会存在的问题

int main()
{
	int i = 1;
	int j = (++i) + (++i) + (++i);
	printf("%d\n", j);
	return 0;
}

上面代码，分别在不同的编译器下试试，可能会得到不同结果

在Linux下测试结果为10，在VS上测试结果为12

本质：是因为上面表达式的"计算路径不唯一"(为什么?编译器识别表达式，是同时加载至寄存器，还是分批加载，完全不确定)导致的，类似这种复杂表达式，不推荐使用。

表达式匹配：贪心算法

编译器在处理复杂表达式的时候，会尽可能将多个运算符组成表达式进行运算

int main()
{
	int a = 10;
	int b = 20;
	//printf("%d\n", a++++ + b);//自动匹配失败 err
	printf("%d\n", a++ + ++b); //自行分离匹配，非常不推荐，不过能看出空格的好处 31
	return 0;
}

11.符号

深度理解取余/取模运算

step 1:向0取整

int main()
{
	int i = -2.9;
	int j = 2.9;
	printf("%d\n", i); //结果是：-2
	printf("%d\n", j); //结果是：2
	return 0;
}

 如图所示：

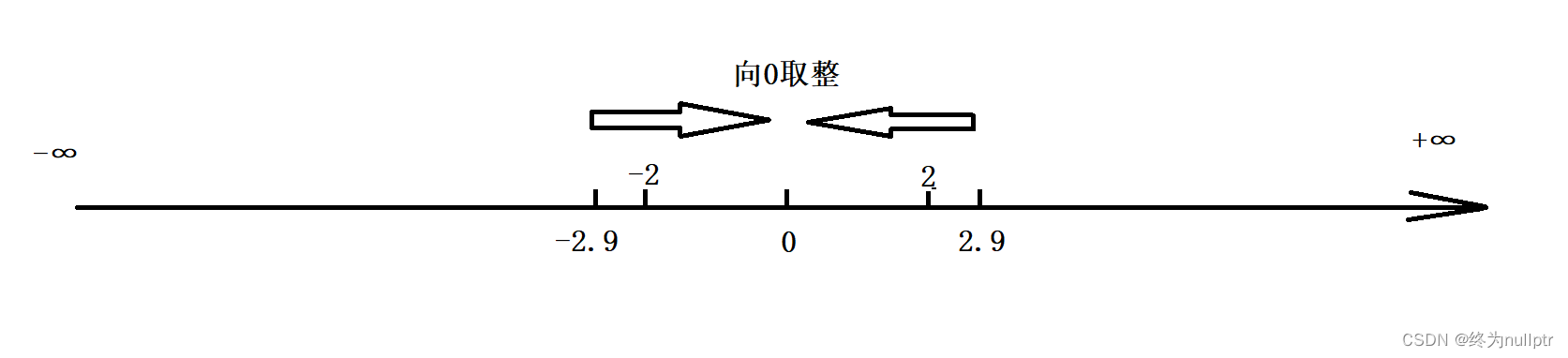
在库中有一个trunc取整函数，同作用：

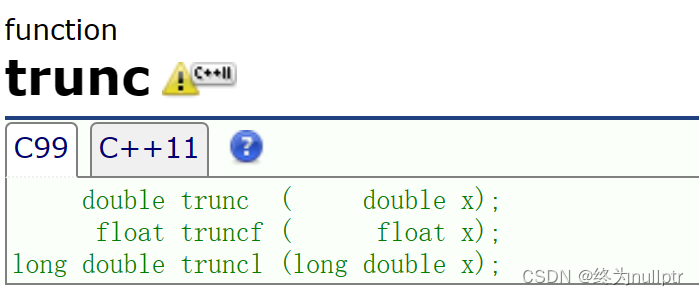
#include<math.h>
int main()
{
	printf("%d\n",(int)trunc(-2.9));
	printf("%d\n", (int)trunc(2.9));
	return 0;
}

step 2:向-∞取整

如图所示：

int main()
{
	//本质是向-∞取整，注意输出格式要不然看不到结果
	printf("%.1f\n", floor(-2.9));
	printf("%.1f\n", floor(-2.1));
	printf("%.1f\n", floor(2.9));
	printf("%.1f\n", floor(2.1));
	return 0;
}

 step3:向+∞取整

如图所示：

int main()
{
	//本质是向+∞取整，注意输出格式要不然看不到结果
	printf("%.1f\n", ceil(-2.9));
	printf("%.1f\n", ceil(-2.1));
	printf("%.1f\n", ceil(2.9));
	printf("%.1f\n", ceil(2.1));
	return 0;
}

 

step4:四舍五入 

int main()
{
	//本质是四舍五入
	printf("%.1f\n", round(2.1));
	printf("%.1f\n", round(2.9));
	printf("%.1f\n", round(-2.1));
	printf("%.1f\n", round(-2.9));
	return 0;
}

 取模概念：

如果a和d是两个自然数，d非零，可以证明存在两个唯一的整数 q 和 r，满足 a = q*d + r 且0 ≤ r < d。其中，q被称为商，r 被称为余数。

int main()
{
	int a = 10;
	int d = 3;
	printf("%d\n", a % d); //结果是1
	//因为：a=10,d=3,q=3,r=1   0<= r <d(3)
	//所以：a = q*d+r -> 10=3*3+1
	return 0;
}

如果是下面的代码呢?

int main()
{
	int a = -10;
	int d = 3;
	printf("%d\n", a % d); //结果是-1
	return 0;
}

python环境：

 结论：很显然，上面关于取模的定义，并不能满足语言上的取模运算

因为在C中，现在-10%3出现了负数，根据定义：满足 a = q*d + r 且0 ≤ r < d，C语言中的余数，是不满足定义的，因为，r<0了。

故，大家对取模有了一个修订版的定义：
如果a和d是两个自然数，d非零，可以证明存在两个唯一的整数 q 和 r，满足 a = q*d + r , q 为整数，且0 ≤ |r|< |d|。其中，q 被称为商，r 被称为余数。

有了这个新的定义，那么C中或者Python中的“取模”，就都能解释了。
解释C: -10 = (-3) * 3 + (-1)
解释Python：-10 = （?）* 3 + 2,其中，可以推到出来,'?'必须是-4(后面验证).即-10 = （-4）* 3 + 2，才能满足定义。

所以，在不同语言，同一个计算表达式，负数“取模”结果是不同的。我们可以称之为分别叫做正余数 和 负余数

由上面的例子可以看出，具体余数r的大小，本质是取决于商q的。而商，又取决谁呢？取决于除法计算的时候，取整规则。

本质 1 取整：
取余：尽可能让商，进行向0取整。
取模：尽可能让商，向-∞方向取整。

故：
C中%,本质其实是取余。
Python中%，本质其实是取模。

理解链：
对任何一个大于0的数，对其进行0向取整和-∞取整，取整方向是一致的。故取模等价于取余
对任何一个小于0的数，对其进行0向取整和-∞取整，取整方向是相反的。故取模不等价于取余

同符号数据相除，得到的商，一定是正数（正数vs正整数），即大于0！故，在对其商进行取整的时候，取模等价于取余。

计算数据同符号：

C:

int main()
{
	printf("%d\n", 10 / 3);
	printf("%d\n\n", 10 % 3);
	printf("%d\n", -10 / -3);
	printf("%d\n\n", -10 % -3);
	return 0;
}

 python:

print(10 // 3)
print(10 % 3)
print(-10 // -3)
print(-10 % -3)

注：python中 / 默认是浮点数除法，//才是整数除法，并进行-∞取整 

通过对比试验，更加验证了，参与取余的两个数据，如果同符号，取模等价于取余

如果参与运算的数据，不同符号呢？

C:

int main()
{
	printf("%d\n", -10 / 3); //结果：-3
	printf("%d\n\n", -10 % 3); //结果：-1 -> -10=(-3)*3+(-1)
	printf("%d\n", 10 / -3);//结果：-3
	printf("%d\n\n", 10 % -3);//结果：1 -> 10=(-3)*(-3)+1
	return 0;
}

python:

print(-10 // 3)
print(-10 % 3)
print(10 // -3)
print(10 % -3)

重新看看定义：
如果a和d是两个自然数，d非零，可以证明存在两个唯一的整数 q 和 r，满足 a = q*d + r , q 为整数，且0 ≤ |r|< |d|。其中，q 被称为商，r 被称为余数。

a = q*d + r 变换成 r = a - q*d 变换成 r = a + (-q*d) ,对于：x = y + z，这样的表达式，x的符号 与 |y|、|z|中大的数据一致

而r = a + (-q*d)中，|a| 和 |-q*d|的绝对值谁大，取决于商q的取整方式。
c是向0取整的，也就是q本身的绝对值是减小的。
如：
-10/3=-3.333.33 向0取整 -3.  a=-10 |10|, -q*d=-(-3)*3=9 |9|
10/-3=-3.333.33 向0取整 -3.  a=10 |10|, -q*d=-(-3)*(-3)=-9 |9|
绝对值都变小了
python是向-∞取整的，也就是q本身的绝对值是增大的。
-10/3=-3.333.33  '//'向-∞取整 -4.  a=-10 |10|, -q*d=-(-4)*3=12 |12|
10/-3=--3.333.33 '//'向-∞取整 -4.  a=10 |10|, -q*d=-(-4)*(-3)=-12 |12|
绝对值都变大了

结论：如果参与取余的两个数据符号不同，在C语言中(或者其他采用向0取整的语言如：C++，Java)，余数符号，与被除数相同。

总结：

浮点数(或者整数相除)，是有很多的取整方式的。
如果a和d是两个自然数，d非零，可以证明存在两个唯一的整数 q 和 r，满足 a = q*d + r , q 为整数，且0 ≤ |r|< |d|。其中，q 被称为商，r 被称为余数。
在不同语言，同一个计算表达式，“取模”结果是不同的。我们可以称之为分别叫做正余数和负余数
具体余数r的大小，本质是取决于商q的。而商，又取决于除法计算的时候，取整规则。
取余vs取模： 取余尽可能让商，进行向0取整。取模尽可能让商，向-∞方向取整。
参与取余的两个数据，如果同符号，取模等价于取余
如果参与取余的两个数据符号不同，在C语言中(或者其他采用向0取整的语言如：C++，Java)，余数符号，与被除数相同。（因为采用的向0取整）