Overview 概述

1. 时间复杂度为 O(nlogn) ;
2. 适合大规模的数据排序 ;
3. 相比于冒泡排序、插入排序、选择排序这三种排序算法, 更加常用 ;
4. 用到了分治思想(即分而治之, 英文叫 “Divide and conquer”)，非常巧妙 ;
5. 英文名称: Merge Sort ;

• 分治思想, 在很多领域都有广泛的应用，例如算法领域有分治算法（归并排序、快速排序都属于分治算法，二分法查找也是一种分治算法）;
• 分治算法一般都是用"递归"来实现的 (分治是一种解决问题的处理思想，递归是一种编程技巧) ;

Principle 原理

main idea 核心思想

如果要排序一个数组，我们先把数组从中间分成前后两部分，然后对前后两部分分别排序 (递归使用同样的归并排序)，再将排好序的两部分合并在一起，这样整个数组就都有序了。

decomposition diagram 分解示意图

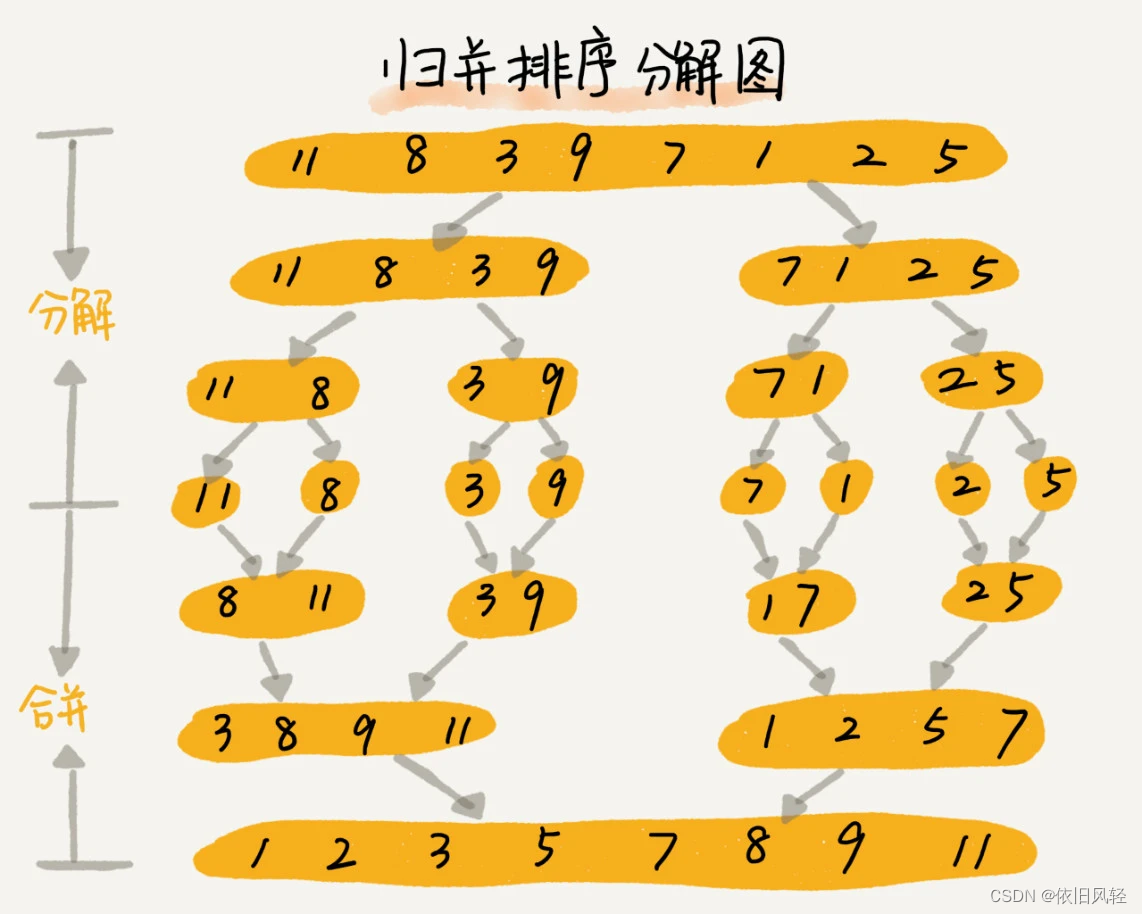
用递归代码来实现归并排序

// 递推公式：
merge_sort(p…r) = merge(merge_sort(p…q), merge_sort(q+1…r))
// 终止条件 (不用再继续分解)
p >= r 

merge_sort(p…r) 表示，给下标从 p 到 r 之间的数组排序。我们将这个排序问题转化为了两个子问题，merge_sort(p…q) 和 merge_sort(q+1…r)，其中下标 q 等于 p 和 r 的中间位置，也就是 (p+r)/2。当下标从 p 到 q 和从 q+1 到 r 这两个子数组都排好序之后，我们再将两个有序的子数组合并在一起，这样下标从 p 到 r 之间的数据就也排好序了。

Show The Swift Code

class Solution {
    func sortArray(_ nums: [Int]) -> [Int] {
        var numbers = nums.map { $0 }
        mergeSort(&numbers, 0, numbers.count - 1)
        return numbers
    }
    
    final func mergeSort(_ numbers: inout [Int], _ leading: Int, _ trailing: Int) {
        guard leading < trailing else { return }
        // 取中间的索引
        let mid = (trailing + leading) >> 1
        // 左侧递归排序
        mergeSort(&numbers, leading, mid)
        // 右侧递归排序
        mergeSort(&numbers, mid + 1, trailing)
        // 合并两个有序区间
        merge(&numbers, leading, trailing, mid)
    }
    
    private final func merge(_ numbers: inout [Int], _ leading: Int, _ trailing: Int, _ mid: Int) {
        var i = leading
        var j = mid + 1
        var tmp = [Int]()
        // 比较分区的首个元素
        while i <= mid, j <= trailing {
            if numbers[i] < numbers[j] {
                tmp.append(numbers[i])
                i = i + 1
            } else {
                tmp.append(numbers[j])
                j = j + 1
            }
        }
        // 将左分区的剩余的元素依次添加到tmp
        while i <= mid {
            tmp.append(numbers[i])
            i = i + 1
        }
        // // 将右分区的剩余的元素依次添加到tmp
        while j <= trailing {
            tmp.append(numbers[j])
            j = j + 1
        }
        // 将完成合并的两个分区, 回写到numbers
        for idx in 0...(trailing - leading) {
            numbers[idx + leading] = tmp[idx]
        }
    }
}

合并分区函数merge(_ numbers: [Int], _ leading: Int, _ trailing: Int, _ mid: Int)

这个函数的作用就是，将已经有序的 numbers[leading...mid] 和 numbers[mid+1....trailing] 合并成一个有序的数组，并且放入 numbers[leading....trailing]。那这个过程具体该如何做呢？如下图所示，每次调用需要申请一个临时数组 tmp。我们用两个游标 i 和 j，分别指向两个分区的第一个元素。比较这两个元素 numbers[i]和 numbers[j]，如果 numbers[i]<=numbers[j]，我们就把 numbers[i]放入到临时数组 tmp，并且 i 后移一位，否则将 numbers[j]放入到数组 tmp，j 后移一位。继续上述比较过程，直到其中一个子数组中的所有数据都放入临时数组中，再把另一个数组中的数据依次加入到临时数组的末尾，这个时候，临时数组中存储的就是两个子数组合并之后的结果了。最后再把临时数组 tmp 中的数据拷贝到原数组区间 numbers[leaing...trailing]中。

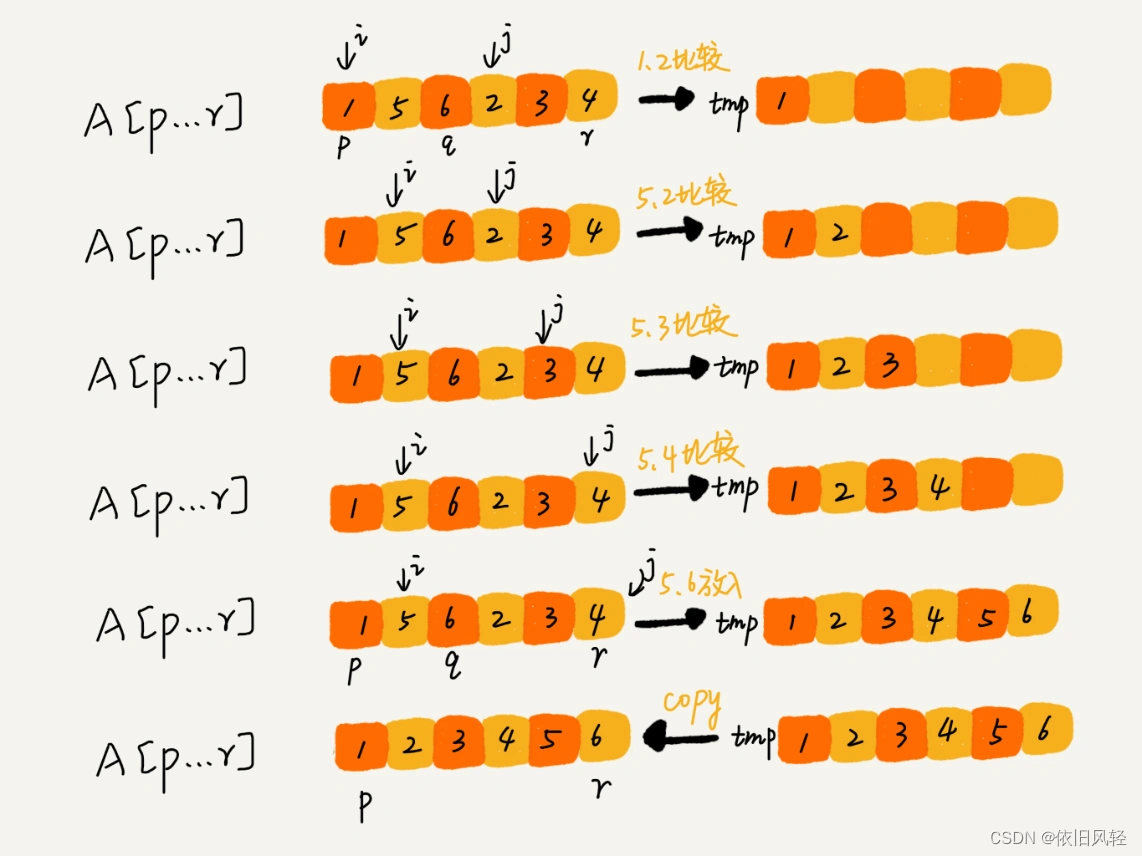
Performance analysis 性能分析

是否为稳定排序 ?

是, 前提是合并分区时, 当两个分区中相互比对的元素大小相同, 将 leading 分区的元素加入 tmp.

时间复杂度是多少？

$$O(nlogn)$$

看了几篇Blog, 感觉证明过程都不严谨, 知道怎样证明的欢迎指教🫰🏻

归并排序的执行效率与要排序的原始数组的有序程度无关，所以其时间复杂度是非常稳定的，不管是最好情况、最坏情况，还是平均情况，时间复杂度都是 O(nlogn)。

空间复杂度

$$O(n)$$
归并排序的时间复杂度任何情况下都是 O(nlogn)，看起来非常优秀。（即便是快速排序，最坏情况下，时间复杂度也达到了 O(n2)。）但是，归并排序并没有像快排那样，应用广泛，这是为什么呢？因为它有一个致命的“弱点”，那就是归并排序不是原地排序算法。

这是因为归并排序的合并函数，在合并两个有序区间为一个有序区间时，需要借助额外的存储空间tmp。尽管每次合并操作都需要申请额外的内存空间，但在合并完成之后，临时开辟的内存空间就被释放掉了。在任意时刻，CPU 只会有一个函数在执行，也就只会有一个临时的内存空间在使用。临时内存空间最大也不会超过 n 个数据的大小，所以空间复杂度是 O(n)。