双周赛99

难度简单4

给你一个正整数 num ，请你将它分割成两个非负整数 num1 和 num2 ，满足：

• num1
  

  和

  num2
  

  直接连起来，得到

  num
  

  各数位的一个排列。

  • 换句话说，num1 和 num2 中所有数字出现的次数之和等于 num 中所有数字出现的次数。

• num1 和 num2 可以包含前导 0 。

请你返回 num1 和 num2 可以得到的和的 最小 值。

注意：

• num 保证没有前导 0 。
• num1 和 num2 中数位顺序可以与 num 中数位顺序不同。

示例 1：

输入：num = 4325
输出：59
解释：我们可以将 4325 分割成 num1 = 24 和 num2 = 35 ，和为 59 ，59 是最小和。

示例 2：

输入：num = 687
输出：75
解释：我们可以将 687 分割成 num1 = 68 和 num2 = 7 ，和为最优值 75 。

提示：

• 10 <= num <= 109

难度中等2

有一个无穷大的二维网格图，一开始所有格子都未染色。给你一个正整数 n ，表示你需要执行以下步骤 n 分钟：

• 第一分钟，将 任一 格子染成蓝色。
• 之后的每一分钟，将与蓝色格子相邻的 所有 未染色格子染成蓝色。

下图分别是 1、2、3 分钟后的网格图。

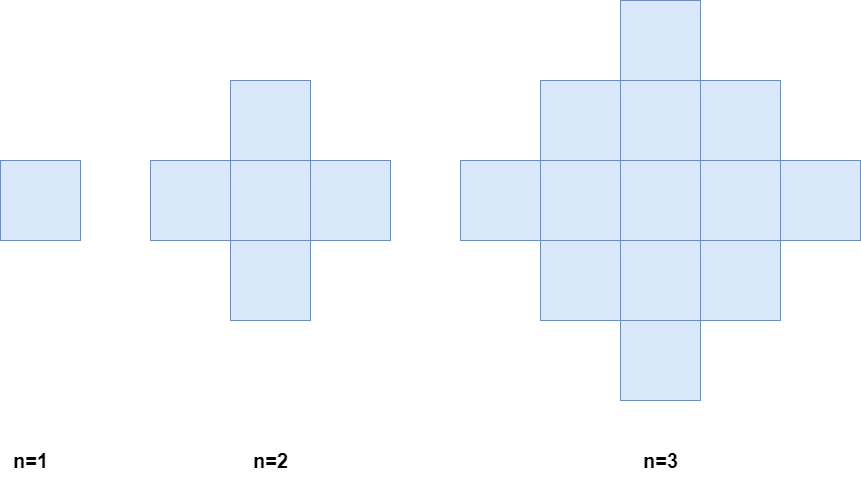
请你返回 n 分钟之后 被染色的格子 数目。

示例 1：

输入：n = 1
输出：1
解释：1 分钟后，只有 1 个蓝色的格子，所以返回 1 。

示例 2：

输入：n = 2
输出：5
解释：2 分钟后，有 4 个在边缘的蓝色格子和 1 个在中间的蓝色格子，所以返回 5 。

提示：

• 1 <= n <= 105

难度中等8

给你一个二维整数数组 ranges ，其中 ranges[i] = [starti, endi] 表示 starti 到 endi 之间（包括二者）的所有整数都包含在第 i 个区间中。

你需要将 ranges 分成 两个 组（可以为空），满足：

• 每个区间只属于一个组。
• 两个有 交集 的区间必须在 同一个 组内。

如果两个区间有至少 一个 公共整数，那么这两个区间是 有交集 的。

• 比方说，区间 [1, 3] 和 [2, 5] 有交集，因为 2 和 3 在两个区间中都被包含。

请你返回将 ranges 划分成两个组的 总方案数 。由于答案可能很大，将它对 109 + 7 取余 后返回。

示例 1：

输入：ranges = [[6,10],[5,15]]
输出：2
解释：
两个区间有交集，所以它们必须在同一个组内。
所以有两种方案：
- 将两个区间都放在第 1 个组中。
- 将两个区间都放在第 2 个组中。

示例 2：

输入：ranges = [[1,3],[10,20],[2,5],[4,8]]
输出：4
解释：
区间 [1,3] 和 [2,5] 有交集，所以它们必须在同一个组中。
同理，区间 [2,5] 和 [4,8] 也有交集，所以它们也必须在同一个组中。
所以总共有 4 种分组方案：
- 所有区间都在第 1 组。
- 所有区间都在第 2 组。
- 区间 [1,3] ，[2,5] 和 [4,8] 在第 1 个组中，[10,20] 在第 2 个组中。
- 区间 [1,3] ，[2,5] 和 [4,8] 在第 2 个组中，[10,20] 在第 1 个组中。

提示：

• 1 <= ranges.length <= 105
• ranges[i].length == 2
• 0 <= starti <= endi <= 109

class Solution {
    //假设最后分成了 m 个集合，那么每个集合都可以决定要在第一个组还是第二个组，
    // 所以方案数为 2 ^ m
    private static final int MOD = (int)1e9 + 7;
    public int countWays(int[][] ranges) {
        Arrays.sort(ranges, (a,b) -> a[0] == b[0] ? a[1]-b[1] : a[0] - b[0]);
        int ans = 2;
        int maxR = ranges[0][1];
        for(int[] p : ranges){
            if(p[0] > maxR){ // 产生了新的集合 m加一
                ans = ans * 2 % MOD;
            }
            maxR = Math.max(maxR, p[1]);
        }
        return ans;
    }
}

难度中等1815

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回 一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间 。

示例 1：

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

示例 2：

输入：intervals = [[1,4],[4,5]]
输出：[[1,5]]
解释：区间 [1,4] 和 [4,5] 可被视为重叠区间。

提示：

• 1 <= intervals.length <= 104
• intervals[i].length == 2
• 0 <= starti <= endi <= 104

class Solution {
    public int[][] merge(int[][] intervals) {
        Arrays.sort(intervals, (a, b) -> a[0] == b[0] ? a[1]-b[1] : a[0]-b[0]);
        List<int[]> list = new ArrayList<>();
        int i = 0;
        while(i < intervals.length){
            int left = intervals[i][0];
            int right = intervals[i][1];
            while(i+1 < intervals.length && right >= intervals[i+1][0]){
                right = Math.max(right, intervals[i+1][1]);
                i++;
            }
            list.add(new int[]{left, right});
            i++;
        }
        int[][] res = new int[list.size()][2];
        for(int k = 0; k < list.size(); k++){
            res[k] = list.get(k);
        }
        return res;
    }
}

难度困难13

Alice 有一棵 n 个节点的树，节点编号为 0 到 n - 1 。树用一个长度为 n - 1 的二维整数数组 edges 表示，其中 edges[i] = [ai, bi] ，表示树中节点 ai 和 bi 之间有一条边。

Alice 想要 Bob 找到这棵树的根。她允许 Bob 对这棵树进行若干次 猜测 。每一次猜测，Bob 做如下事情：

• 选择两个 不相等 的整数 u 和 v ，且树中必须存在边 [u, v] 。
• Bob 猜测树中 u 是 v 的 父节点 。

Bob 的猜测用二维整数数组 guesses 表示，其中 guesses[j] = [uj, vj] 表示 Bob 猜 uj 是 vj 的父节点。

Alice 非常懒，她不想逐个回答 Bob 的猜测，只告诉 Bob 这些猜测里面 至少 有 k 个猜测的结果为 true 。

给你二维整数数组 edges ，Bob 的所有猜测和整数 k ，请你返回可能成为树根的 节点数目 。如果没有这样的树，则返回 0。

示例 1：

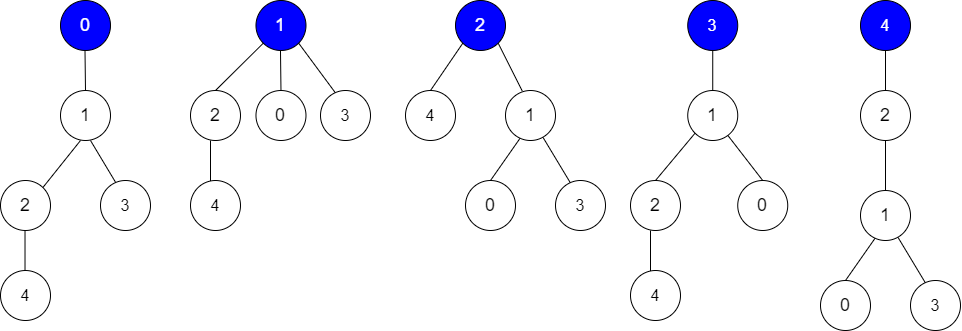
输入：edges = [[0,1],[1,2],[1,3],[4,2]], guesses = [[1,3],[0,1],[1,0],[2,4]], k = 3
输出：3
解释：
根为节点 0 ，正确的猜测为 [1,3], [0,1], [2,4]
根为节点 1 ，正确的猜测为 [1,3], [1,0], [2,4]
根为节点 2 ，正确的猜测为 [1,3], [1,0], [2,4]
根为节点 3 ，正确的猜测为 [1,0], [2,4]
根为节点 4 ，正确的猜测为 [1,3], [1,0]
节点 0 ，1 或 2 为根时，可以得到 3 个正确的猜测。

示例 2：

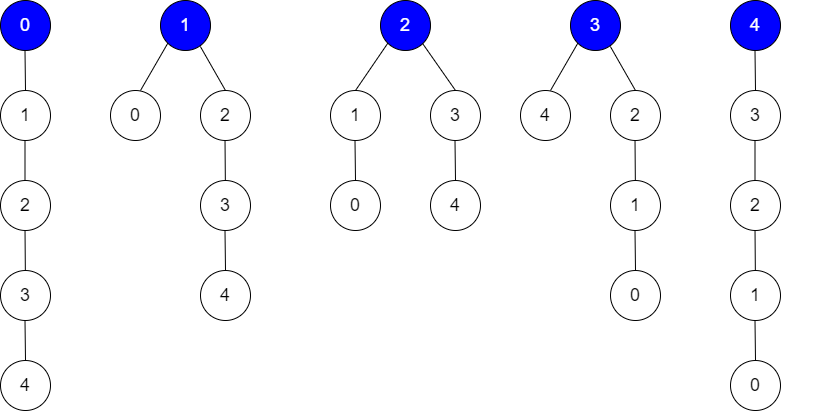
输入：edges = [[0,1],[1,2],[2,3],[3,4]], guesses = [[1,0],[3,4],[2,1],[3,2]], k = 1
输出：5
解释：
根为节点 0 ，正确的猜测为 [3,4]
根为节点 1 ，正确的猜测为 [1,0], [3,4]
根为节点 2 ，正确的猜测为 [1,0], [2,1], [3,4]
根为节点 3 ，正确的猜测为 [1,0], [2,1], [3,2], [3,4]
根为节点 4 ，正确的猜测为 [1,0], [2,1], [3,2]
任何节点为根，都至少有 1 个正确的猜测。

提示：

• edges.length == n - 1
• 2 <= n <= 105
• 1 <= guesses.length <= 105
• 0 <= ai, bi, uj, vj <= n - 1
• ai != bi
• uj != vj
• edges 表示一棵有效的树。
• guesses[j] 是树中的一条边。
• 0 <= k <= guesses.length