数据结构与算法（七）：排序算法

news2024/10/7 10:23:57

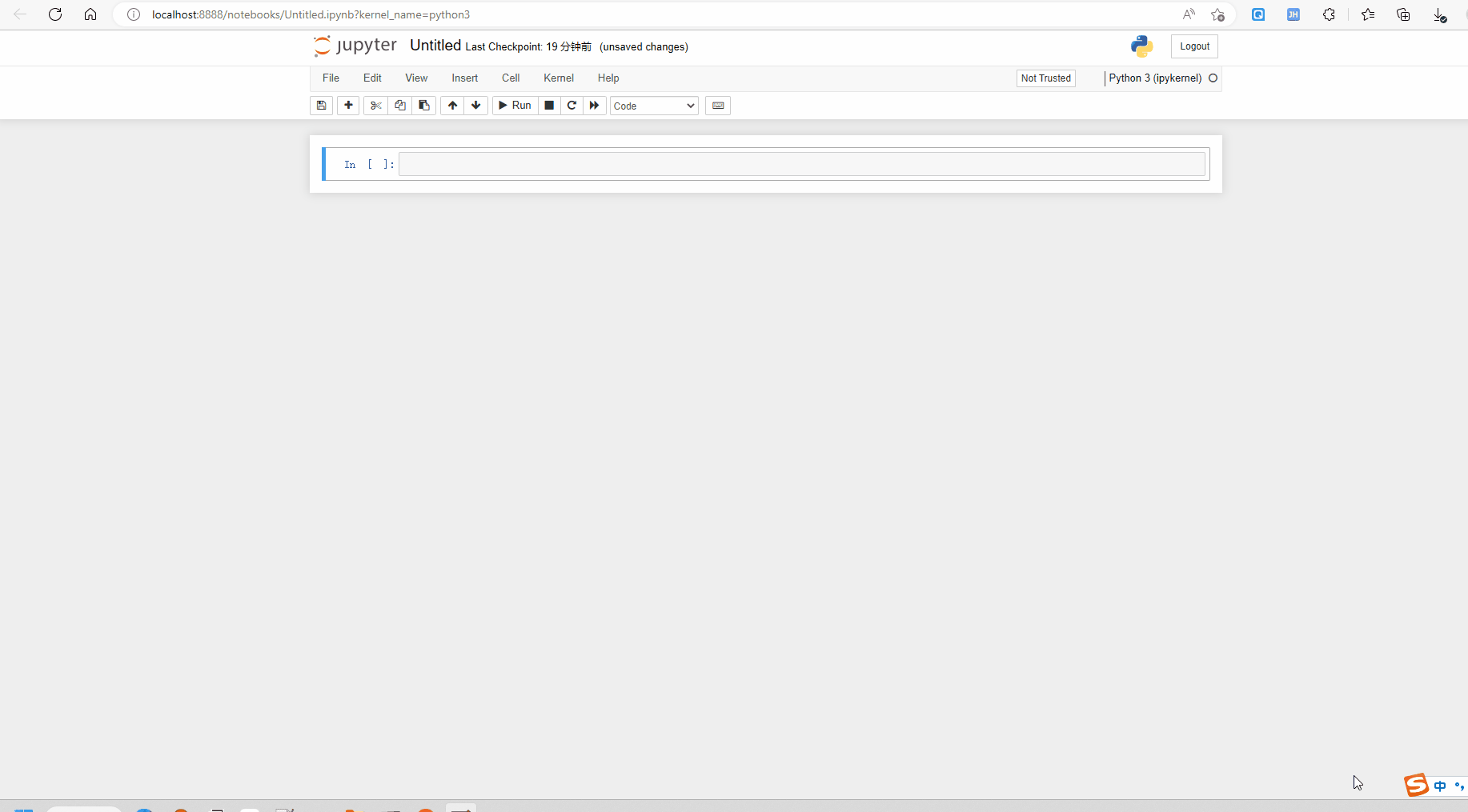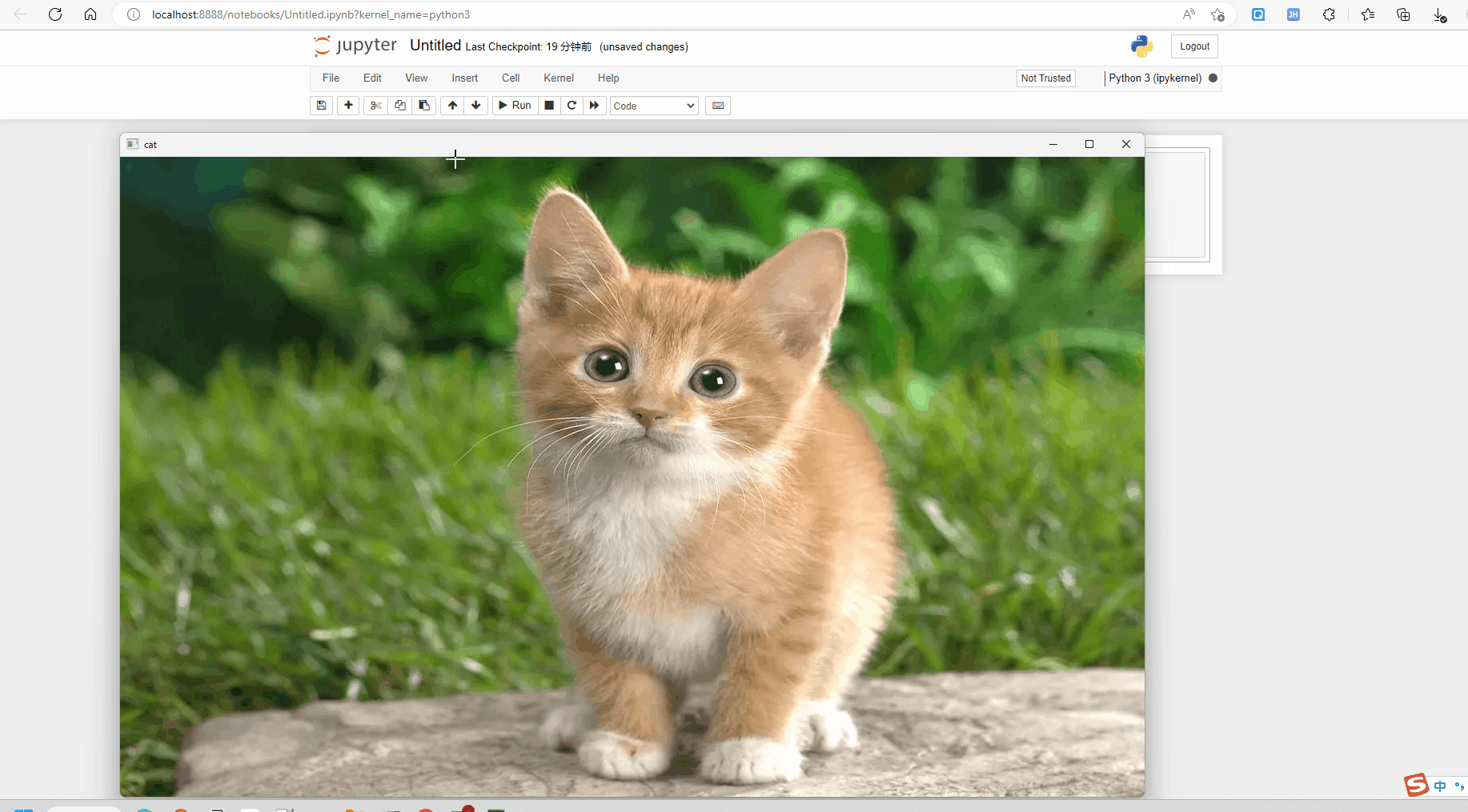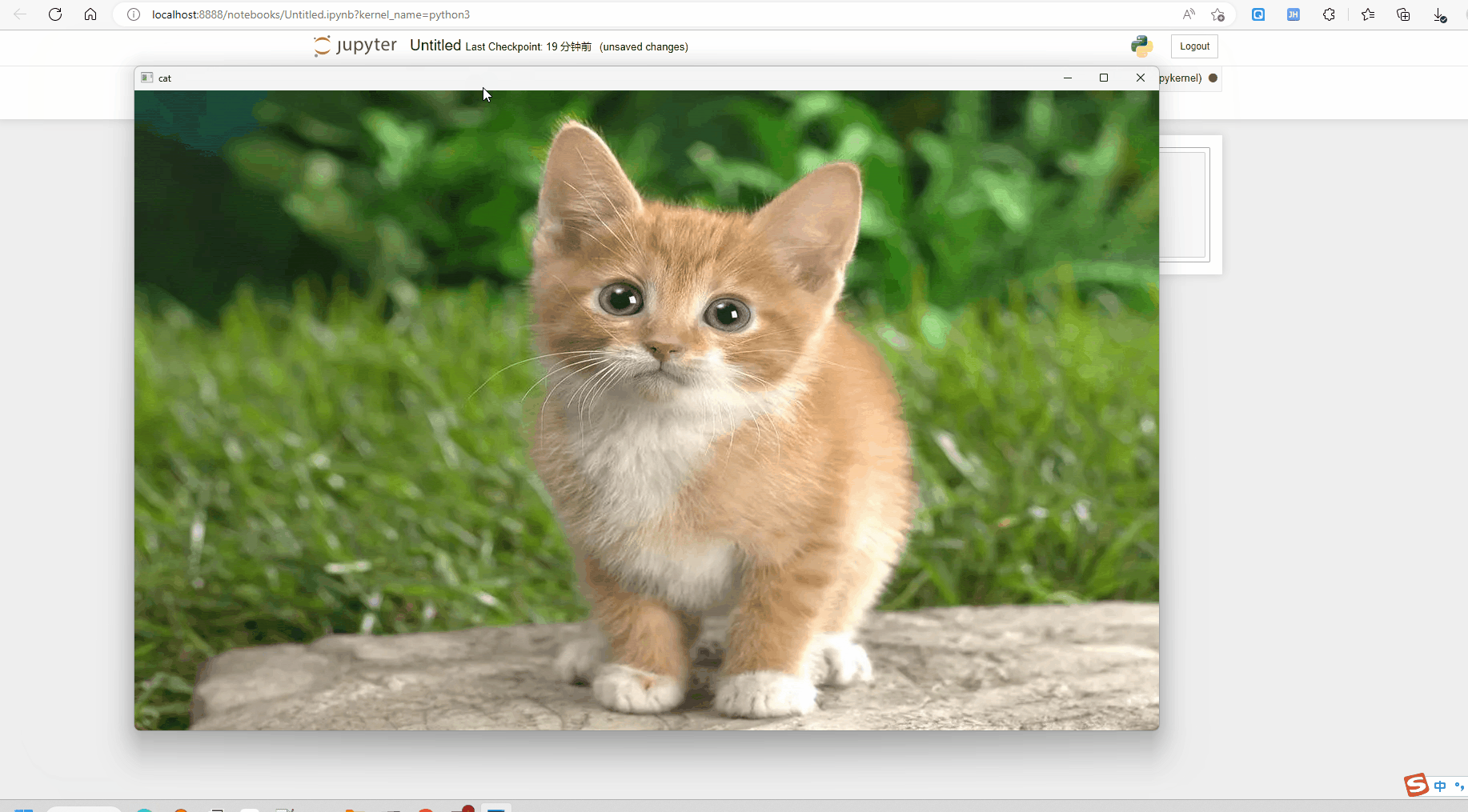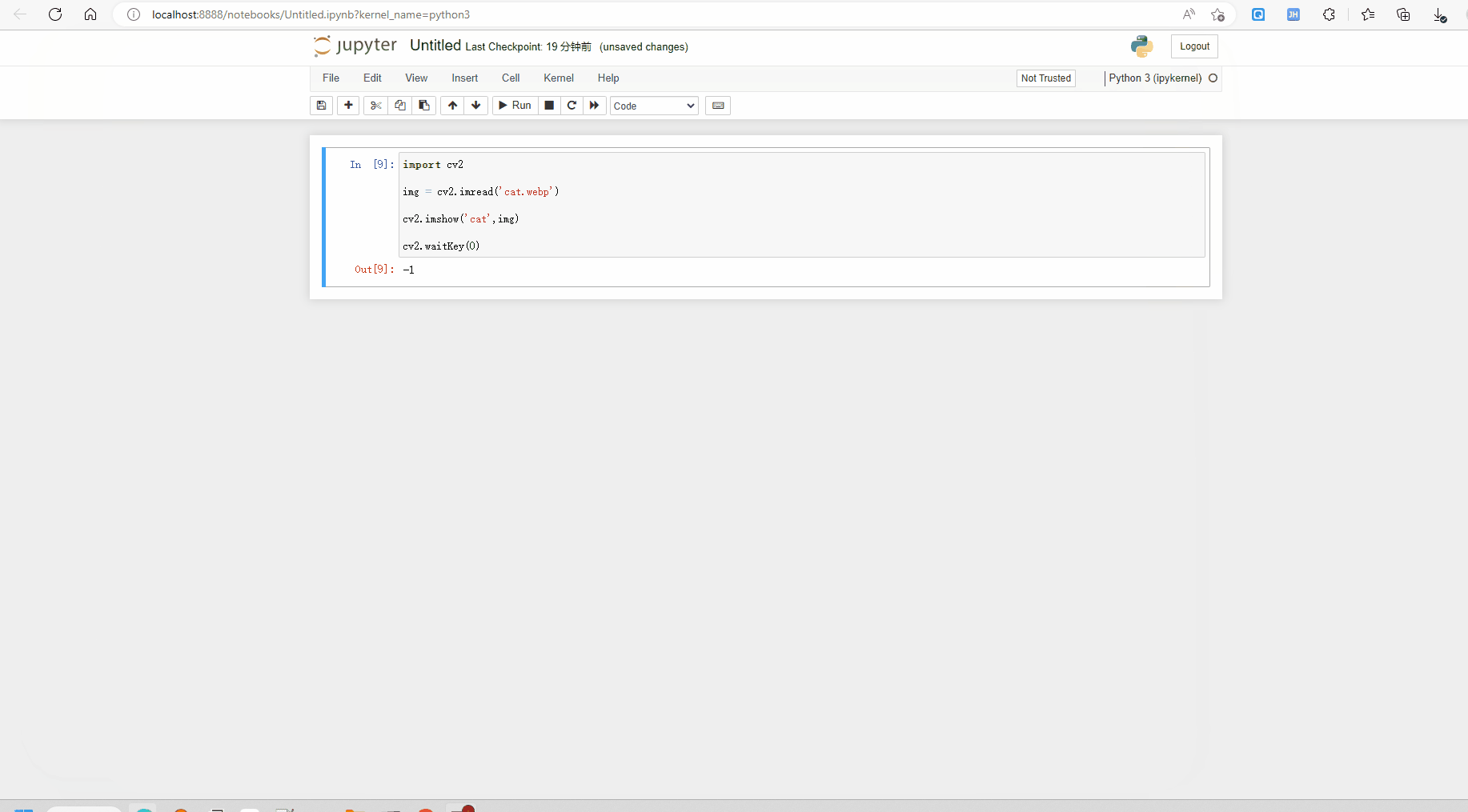
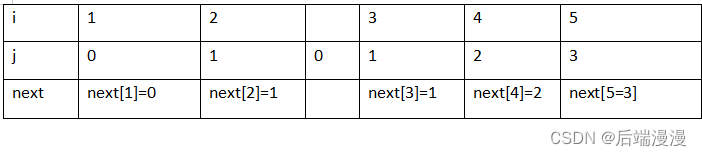
排序算法是《数据结构与算法》中最基本的算法之一，排序算法可以分为内部和外部排序。

  • 内部排序：数据记录在内存中进行排序。

  • 外部排序：因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。

常见排序算法：插入排序、希尔排序、选择排序、冒泡排序、快速排序、堆排序、基数排序等。

在这里插入图片描述

说明：由于对对象元素进行排序需要实现Comparable接口，这里为了实现简单，方便测试，仅对整数进行排序（即排序的对象为整型数组）。

一、插入排序

排序思想：把待排序的元素按其值的大小逐个插入到一个已经排好序的序列中，直到所有的元素插入完为止。

排序过程：

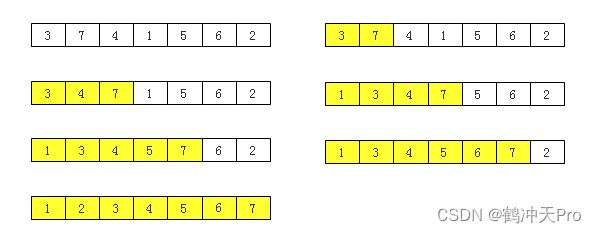
在这里插入图片描述

1.1、直接插入排序

其代码如下：

//核心代码
public void sort(int[] data) {
    int size = data.length;
    for (int i = 1; i < size; i++) {
        for (int j = i; j >= 1 && data[j] < data[j-1]; j--) {
             swap(data, j, j-1);
        }
    }
}

//交换两个元素
public void swap(int[] data,int i,int j) {
    int temp = data[i];
    data[i] = data[j];
    data[j] = temp;
}

在内循环中将较大的元素一次性向右移动而不是交换两个元素，这样访问数组的次数将减半 。其代码如下：

public void sort(int[] data) {
    int size = data.length;
    for (int i = 1; i < size; i++) {
        int temp = data[i];
        int index = 0; //要插入的位置
        for (int j = i; j >= 1; j--) {
            if (temp < data[j-1]) {
                data[j] = data[j-1];
            }else {
                index = j;
                break;
            }
        }
        data[index] = temp;
    }
}

1.2、二分插入排序

将直接插入排序中寻找a[i]插入位置的方法改为二分查找，然后再一次性向右移动元素。

public void sort(int[] data) {
    int size = data.length;
    for (int i = 1; i < size; i++) {
        int num = binaryFind(data, data[i], 0, i-1);
        int temp = data[i];
        //num后的元素向后移动
        for (int j = i; j > num; j--) {
           data[j] = data[j-1];
        }
        data[num] = temp;
    }
}

//找出元素应在数组中插入的位置
public int binaryFind(int[] data, int temp, int down, int up) {
    if(up<down || up>data.length || down<0) {
        System.out.println("下标错误");
    }
    if(temp < data[down]) return down;
    if(temp > data[up]) return up+1;
    int mid = (up-down)/2 + down;
    if(temp == data[mid]) {
        return mid + 1;
    }else if(temp < data[mid]) {
        up = mid-1;
    }else if(temp > data[mid]) {
        down = mid+1;
    }
    return binaryFind(data,temp, down, up);
}

二分插入排序减少了比较次数，特别是当要排序的数据很大时，这个效果将更加明显。

二、选择排序

排序思想：每一次从待排序的数据元素中找出最小（或最大）的一个元素，将它和待排序的元素中第一个位置的元素进行交换，直到全部待排序的数据元素排完程为止。

排序过程：
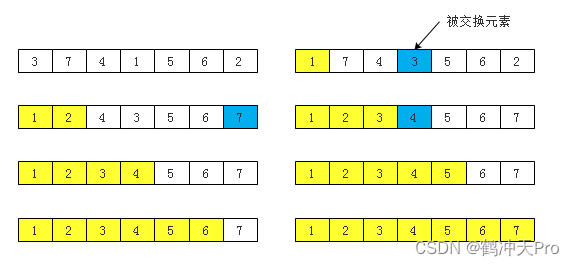
在这里插入图片描述

代码：

public void sort(int[] data) {
    int size = data.length;
    for(int i=0;i<size;i++) {
        int min = i;
        for(int j=i+1;j<size;j++) {
            if(data[j] < data[min]) 
                min=j;
        }
        swap(data,i,min);
    }
}

//交换两个元素
public void swap(int[] data,int i,int j) {
    int temp = data[i];
    data[i] = data[j];
    data[j] = temp;
}

三、冒泡排序

排序思想：依次比较相邻的两个元素，若它们的顺序错误则交换，每次循环都将最大（或最小）元素放在序列一端。

排序过程：

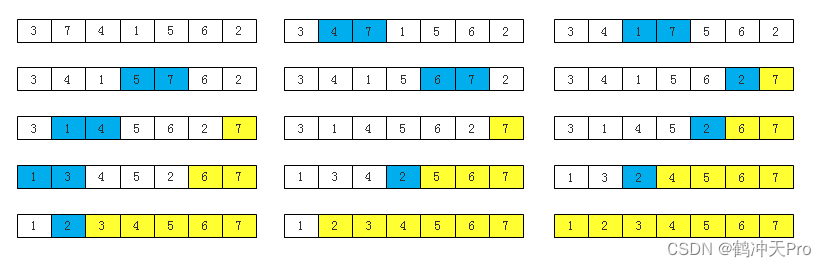
在这里插入图片描述

代码：

public void sort(int[] data) {
    int size = data.length;
    for(int i=0; i<size; i++) {
        for(int j=0; j<size-i-1; j++) {
            if(data[j] > data[j+1]) 
                swap(data,j,j+1);
        }
        
    }
}

//交换两个元素
public void swap(int[] data,int i,int j) {
    int temp = data[i];
    data[i] = data[j];
    data[j] = temp;
}

冒泡排序与选择排序的区别：

  • 冒泡排序法是两两依次比较，并做交换，交换的次数多。
  • 选择排序法是每次循环找出最值，循环结束后将最值调整到合适位置，交换的次数少。

四、归并排序

排序过程：

在这里插入图片描述

4.1、自顶向下的归并排序

排序思想：要将一个数组排序，可以先（递归的）将它分为两半分别排序，然后将结果归并起来。

private int[] array; //辅助数组
public void sort(int[] data) {
    array = new int[data.length];
    mergeSort(data, 0, data.length - 1);

}

//核心算法
public void mergeSort(int[] data, int down, int up) {
    if (up <= down) return; //结束条件
    int mid = (up - down) / 2 + down;
    mergeSort(data, down, mid); //左半边排序
    mergeSort(data, mid + 1, up); //右半边排序
    merge(data, down, mid, up);
}

//一个数组左右半边分别有序，归并
public void merge(int[] data, int down, int mid, int up) {
    int i = down, j = mid + 1;
    //复制数组中元素
    for (int k = down; k <= up; k++) {
        array[k] = data[k];
    }

    for (int k = down; k <= up; k++) {
        if (i > mid) 
            data[k] = array[j++]; //左半边用尽，取右半边元素
        else if (j > up) 
            data[k] = array[i++];
        else if (array[i] < array[j]) //左半边元素比右半边小
            data[k] = array[i++];
        else 
            data[k] = array[j++];
    }
}

对于自顶向下的归并排序的改进：

  • 由于归并排序的方法调用过于频繁，会产生过多的额外开销，所以归并排序在处理小规模问题时，比插入排序要慢。在用归并排序处理大规模数据时，使用插入排序来处理小规模的子数组，一般可使归并排序的运行时间缩短10%-15%。

  • 添加一个判断，如果data[mid]小于data[mid+1],则数组已经有序，不需要进行归并操作。这样可大大减小有序子数组的运行时间。

  • 通过在递归调用的每个层次交换输入数组和辅助数组的角色，节省元素复制到辅助数组中的时间(空间不行）。即在递归中，数据从输入数组排序到辅助数组和从辅助数组排序到输入数组交替使用。

/*
 * 改进自顶向下的归并排序
 * 1. 对小规模数组使用插入排序
 * 2. 加入数组是否有序的判断，减少归并次数
 * 3. 通过在递归中交换参数，避免数组复制
 */
public class MergeInsSort {
    public static final int CUTOFF = 5; //插入排序处理数组长度
    private int[] array;

    public void sort(int[] a) {
        array = a.clone();
        mergeSort(array, a, 0, a.length - 1);

    }

    //核心算法, 对dst进行排序
    public void mergeSort(int[] src, int[] dst, int down, int up) {
        //改进,小规模用插入排序,结束条件
        if (up - down <= CUTOFF) {
            insertionSort(dst, down, up);
            return;
        }
        int mid = (up - down) / 2 + down;
        mergeSort(dst, src, down, mid); //左半边排序，交换输入数组和辅助数组角色
        mergeSort(dst, src, mid + 1, up); //右半边排序，结果：src中有序

        if(src[mid] < src[mid + 1]) { //是否已经有序
            System.arraycopy(src, down, dst, down, up-down+1);
            return;
        }
        merge(src, dst, down, mid, up);
    }

    //一个数组左右半边分别有序，src归并到dst
    public void merge(int[] src, int[] dst, int down, int mid, int up) {
        assert isSorted(src, down, mid);  //断言，左右半边均有序
        assert isSorted(src, mid+1,up);

        int i = down, j = mid + 1;
        for (int k = down; k <= up; k++) {
            if (i > mid) dst[k] = src[j++]; //左半边用尽，取右半边元素
            else if (j > up) dst[k] = src[i++];
            else if (src[i] < src[j]) //左半边元素比右半边小
                dst[k] = src[i++];
            else dst[k] = src[j++];
        }
        assert isSorted(dst, down, up);
    }

    //插入排序
    public void insertionSort(int[] a, int down, int up) {
        for (int i = down+1; i <= up; i++) {
            for (int j = i; j >= down+1 && a[j] < a[j-1]; j--) {
                swap(a, j, j-1);
            }
        }
    }

/*******************************************************************************/

    //交换两个元素
    public void swap(int[] a,int i,int j) {
        int temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
    
    //判断down到up的元素是否有序
    public boolean isSorted(int[] a, int down, int up) {
        for (int i = down+1; i <= up; i++) {
            if (a[i] < a[i - 1])
                return false;
        }
        return true;
    }
}

4.2、自底向上的归并排序

排序思想：先两两归并（把每个元素当成一个长度为1的数组），在四四归并，然后八八归并，一直下去。每轮归并中最后一次归并的第二个数组可能比第一个小（注意不要越界）。

private int[] array; //辅助数组

public void sort(int[] a) {
    array = new int[a.length];
    mergeSort(a);
}

//核心算法
public void mergeSort(int[] a) {
    int N = a.length;
    for (int i = 1; i < N; i = 2 * i) {
        for (int j = 0; j < N - i; j += 2 * i)
            merge(a, j, j + i - 1, Math.min(j + 2 * i - 1, N - 1));
    }
}

//一个数组左右半边分别有序，归并
public void merge(int[] a, int down, int mid, int up) {
    int i = down, j = mid + 1;
    //复制数组中元素
    for (int k = down; k <= up; k++) {
        array[k] = a[k];
    }

    for (int k = down; k <= up; k++) {
        if (i > mid) a[k] = array[j++]; //左半边用尽，取右半边元素
        else if (j > up) a[k] = array[i++];
        else if (array[i] < array[j]) //左半边元素比右半边小
            a[k] = array[i++];
        else a[k] = array[j++];
    }
}

五、希尔排序

排序思想：交换不相邻的元素以对数组的局部进行排序，并最终用插入排序将局部有序的数组排序。使数组中任意间隔为h的元素都是有序的。其中h为任意以1结尾的整数序列。

希尔排序的执行时间依赖于增量序列h，好的增量序列的共同特征：

  • 最后一个增量必须为1；
  • 应该尽量避免序列中的值(尤其是相邻的值)互为倍数的情况。

排序过程：

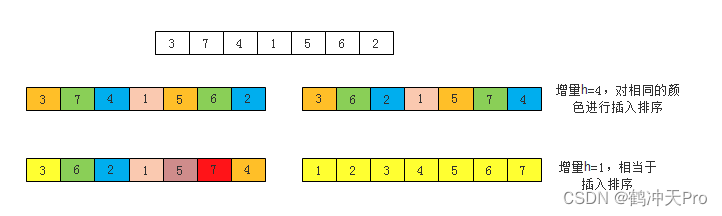
在这里插入图片描述

希尔排序比插入排序要快的多，并且数组越大，优势越大。

代码：

//核心算法，增量序列 1 4 13 ....（3*h+1）
public void sort(int[] data) {
    int size = data.length;
    int h = 1;
    while(h < size/3) 
        h = 3*h + 1;
    while(h > 0 ) {
        //插入排序，间隔h
        for(int i=h; i<size; i++) {
            for(int j=i; j>=h && data[j] < data[j-h]; j = j-h) {
                swap(data, j, j-h);
            }
        }
        h = h/3;
    }

}

//交换两个元素
public void swap(int[] data,int i,int j) {
    int temp = data[i];
    data[i] = data[j];
    data[j] = temp;
}

六、快速排序

排序思想：通过一趟排序将要排序的数据切分成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

切分过程：

在这里插入图片描述

取数组中第一个元素作为切分元素V，从数组的左端开始向右扫描直达找到一个大于等于V的元素，再从数组右端向左扫描直到找到一个小于等于V的元素，交换他们的位置。如此继续，保证左指针左侧的元素都小于等于V，右指针右侧的元素都大于等于V。直到两个指针相遇，将V和左子数组最右侧元素交换，返回j

排序过程：

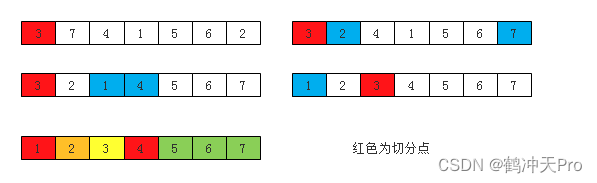
在这里插入图片描述

public void sort(int[] data) {
    sort(data, 0, data.length - 1);
}

//核心算法
public void sort(int[] data, int down, int up) {
    if(up <= down)
        return;
    
    int temp = partition(data, down, up); //找到切分点
    sort(data, down, temp - 1); //左半边排序
    sort(data, temp + 1, up);  //右半边排序
}

//切分
public int partition(int[] data, int down, int up) {
    int i = down;
    int j = up + 1;
    int v = data[down]; //使用data[down]作为切分元素
    while (true) {
        while (data[++i] < v) {
            if (i == up) 
                break;
        }

        while (v < data[--j]) {
            if (j == down) 
                break;
        }

        if (i >= j) break;
        swap(data, i, j);
    }
    swap(data, down, j);
    return j;
}

//交换两个元素
public void swap(int[] data, int i, int j) {
    int temp = data[i];
    data[i] = data[j];
    data[j] = temp;
}

快速排序的改进：

快速排序切分不平衡时可能会非常低效，如：第一次以最小的元素切分，第二次以第二小的元素切分，如此，每次调用只会移动一个元素，这将使快速排序退化为冒泡排序。所以快速排序前要将数组进行随机排序，打乱其顺序。另外对于小规模数组，可以使用插入排序来提高排序的性能。原因和归并排序时一样。

改进后的代码：

//使用插入排序的阙值
public static final int CUTOFF = 5;
public void sort(int[] data) {
    shuffle(data); //打乱数组，消除对输入的依赖
    sort(data, 0, data.length - 1);
}

public void sort(int[] data, int down, int up) {
    //小规模时用插入排序
    if (up - down <= CUTOFF) {
        insertionSort(data, down, up);
        return;
    }
    
  //大规模时使用快速排序
    int temp = partition(data, down, up); //切分
    sort(data, down, temp - 1); //左半边排序
    sort(data, temp + 1, up);  //右半边排序
}

//切分
public int partition(int[] data, int down, int up) {
    int i = down;
    int j = up + 1;
    while (true) {
        //使用data[down]作为切分元素
        while (data[++i] < data[down]) {
            if (i == up) 
                break;
        }

        while (data[down] < data[--j]) {
            if (j == down) 
                break;
        }

        if (i >= j) break;
        swap(data, i, j);
    }
    swap(data, down, j);
    return j;
}

//插入排序
public void insertionSort(int[] data, int down, int up) {
    for (int i = down + 1; i <= up; i++) {
        for (int j = i; j >= down + 1 && data[j] < data[j - 1]; j--) {
            swap(data, j, j - 1);
        }
    }
}

//交换两个元素
public void swap(int[] data, int i, int j) {
    int temp = data[i];
    data[i] = data[j];
    data[j] = temp;
}

//随机打乱数组
public static void shuffle(int[] data) {
    int N = data.length;
    Random rand = new Random();
    for (int i = 0; i < N; i++) {
        int r = i + rand.nextInt(N-i);     // between i and N-1
        int temp = data[i];
        data[i] = data[r];
        data[r] = temp;
    }
}

七、堆排序

排序思想：利用堆的有序性（根节点最大）来进行排序，每次从堆中取出根节点，并保持堆有序。

如果对堆这种数据结构不太了解的话，可以先看我的另一篇博客《数据结构与算法（五），优先队列》。

这里需要注意：这篇博客中实现的堆是从数组中下标为0的位置开始的，所以结点k的子结点下标分别为2k+1和2k+2，这和在《数据结构与算法（五），优先队列》中的堆实现有些不同。

排序过程：

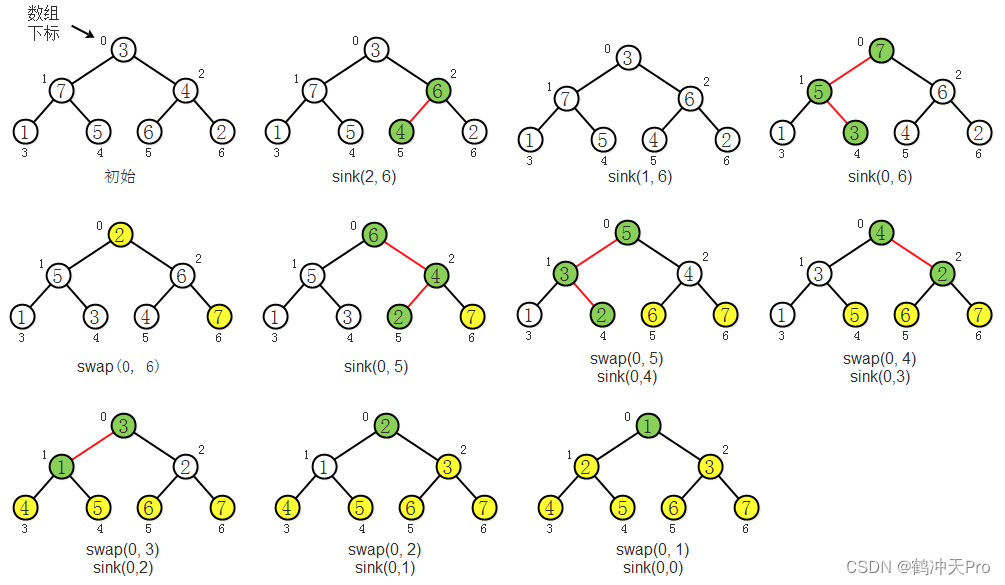
在这里插入图片描述

代码：

public void sort(int[] data) {
    int N = data.length-1;
    for(int k = (N-1)/2; k>=0; k--) {
        sink(data, k, N); //使堆有序
    }
    
    //将最大元素放到最后
    while(N > 0) {
        swap(data, 0, N--);
        sink(data, 0, N);
    }
}

//下沉操作，从下标0开始
private void sink(int[] data, int k, int N) {
    while(2*k+1 <= N) {
        int j = 2*k+1;
        if(j < N && data[j] < data[j+1])
            j++;
        if(data[k] >= data[j])
            break;
        swap(data, k, j);
        k = j;
    }
}

//交换两个元素
public void swap(int[] data, int i, int j) {
    int temp = data[i];
    data[i] = data[j];
    data[j] = temp;
}

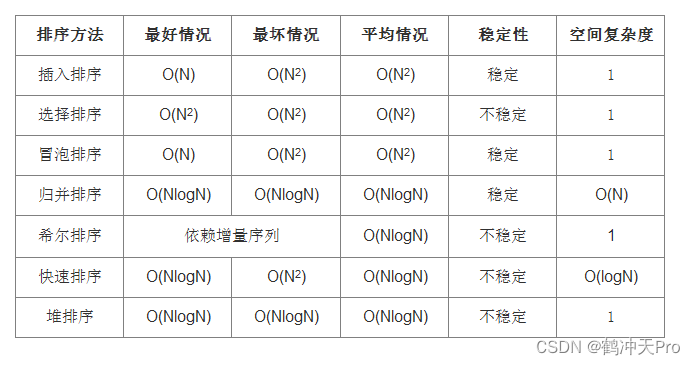
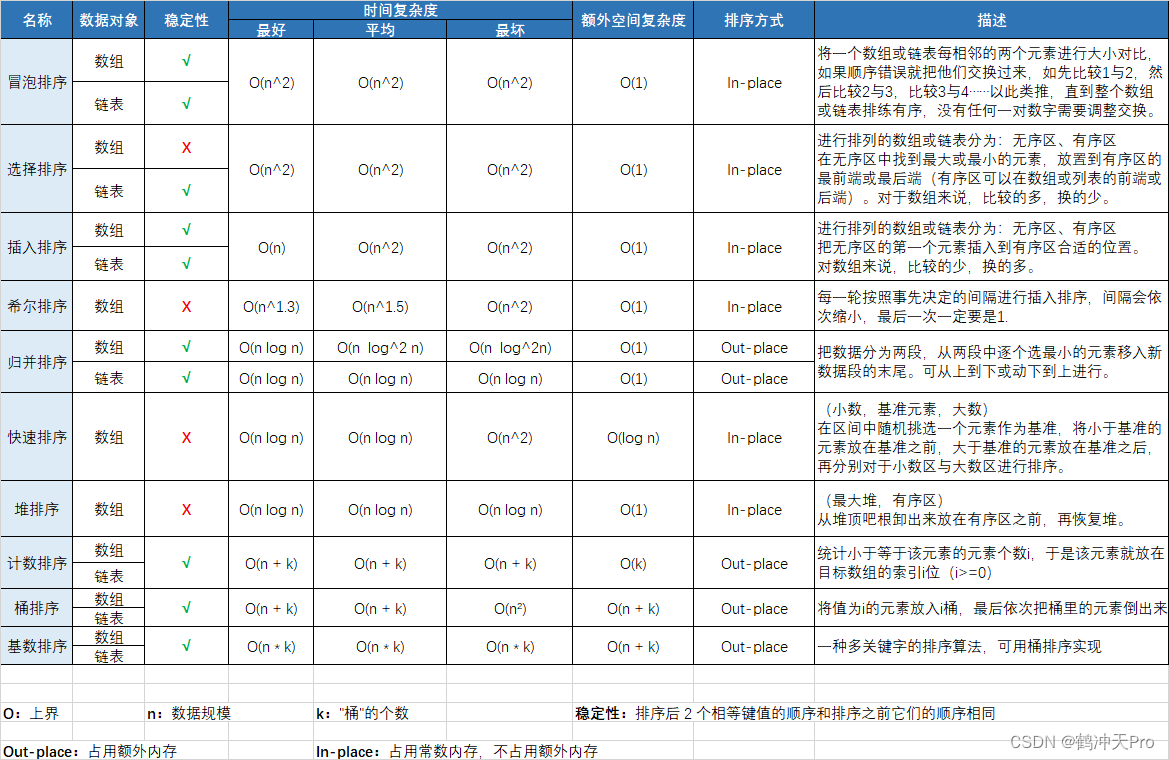
八、性能比较

说明：这里只比较通用的实现方法，而不会对排序方法的改进版本进行比较。

排序的稳定性：

假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，ri=rj，且ri在rj之前，而在排序后的序列中，ri仍在rj之前，则称这种排序算法是稳定的；否则称为不稳定的。

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/390721.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

xgboost:分割Sparsity-aware Split Finding

xgboost:分割Sparsity-aware Split Finding

Sparsity-aware Split Finding1 在许多现实问题中&#xff0c;输入xxx是稀疏的是很常见的。造成稀疏性的可能原因有很多: 1)数据中存在缺失值&#xff1b; 2)统计中频繁出现零项&#xff1b; 3)特征工程的处理结果&#xff0c;如独热编码。 重要的是使算法意识到数据中的稀…
阅读更多...
RocketMQ5.1.0单机安装与启动

RocketMQ5.1.0单机安装与启动

RocketMQ单机安装与启动系统要求下载地址安装步骤RocketMq启动NameServer查看是否启动成功启动BrokerProxy查看是否启动成功修改tool.sh测试消息产生消息的消费关闭服务器系统要求 下载地址 官网下载地址 二进制包是已经编译完成后可以直接运行的&#xff0c;源码包是需要编译…
阅读更多...
javaWeb核心02-RequestResponse

javaWeb核心02-RequestResponse

文章目录Request&Response1&#xff0c;Request和Response的概述2&#xff0c;Request对象2.1 Request继承体系2.2 Request获取请求数据2.2.1 获取请求行数据2.2.2 获取请求头数据2.2.3 获取请求体数据2.2.4 获取请求参数的通用方式基于上述理论&#xff0c;request对象为我…
阅读更多...
python：使用 Jupyter notebook（测试 matplotlib 和 opencv）

python：使用 Jupyter notebook（测试 matplotlib 和 opencv）

环境&#xff1a; window1python 3.10.6 参考&#xff1a; https://jupyter.org/https://opencv.org/ 一、创建虚拟环境 这个步骤可以跳过&#xff08;因为笔者不喜欢在全局环境安装任何东西&#xff0c;所以搞一个新环境&#xff09;。 先选中一个目录&#xff1a;D:\jackl…
阅读更多...
论文笔记 | Conducting research in marketing with quasi-experiments

论文笔记 | Conducting research in marketing with quasi-experiments

这篇论文是Journal of Marketing上的论文&#xff0c;讲了使用准实验来进行论文研究的一些事项。外生性识别的来源、几种准实验方法的注意点还有内生性的解决。 这篇论文对于准实验或者是平常论文的展开有一个非常友善的指导功能&#xff0c;可以阅读~ 摘要&#xff1a;本文旨…
阅读更多...
多线程实现的三种方法、线程名称的获取

多线程实现的三种方法、线程名称的获取

文章目录多线程实现的三种方法1、通过继承Thread&#xff0c;并重写里面的run()方法2、实现Runnable接口&#xff0c;并重写其中run()方法将runnable类传递给Thread类中3、实现Callable接口&#xff0c;重写其中的call()方法Callable接口时有泛型的&#xff0c;该泛型值call()方…
阅读更多...
字符串模式匹配，经典KMP算法你还不会？我可不允许你不会！

字符串模式匹配，经典KMP算法你还不会？我可不允许你不会！

文章目录重点1. 简单模式匹配算法2. 部分匹配值PM的算法&#xff08;Move j-1 PM[j-1]&#xff09;3. 部分匹配值PM的两次改进&#xff08;Move j-next[j]&#xff09;4. 快速得到next数组5. KMP匹配算法重点 童鞋们看网上讲解的时候一定要分清楚序列是从0开始还是从1开始&…
阅读更多...
大数据框架之Hive：第1章 Hive入门

大数据框架之Hive：第1章 Hive入门

1.1 什么是Hive 1&#xff09;Hive简介 Hive是由Facebook开源&#xff0c;基于Hadoop的一个数据仓库工具&#xff0c;可以将结构化的数据文件映射为一张表&#xff0c;并提供类SQL查询功能。 那为什么会有Hive呢&#xff1f;它是为了解决什么问题而诞生的呢&#xff1f; 下…
阅读更多...
性能优化|记一次线上OOM问题处理

性能优化|记一次线上OOM问题处理

概述最近线上监控发现 OOM 涨幅较大&#xff0c;因此去尝试定位和修复这个问题&#xff0c;在修复了一些内存泄漏和大对象占用问题后, OOM 依旧未达到正常标准&#xff0c;在这些新上报的 hprof 文件中&#xff0c;发现几乎所有 case 中都有个叫 FinalizerReference 的对象&…
阅读更多...
集合体系概述以及Collection集合常用API

集合体系概述以及Collection集合常用API

一. 集合 集合与数组类似&#xff0c;都是一种容器。集合是Java中存储对象数据的一种容器。集合也被称为对象容器。 数组的特点 集合的特点 集合的大小不固定&#xff0c;启动后可以动态变化&#xff0c;类型也可以选择不固定。集合更像气球&#xff0c;可大可小。集合非常适合…
阅读更多...
python与pycharm从零安装

python与pycharm从零安装

python&#xff08;解释器&#xff09;下载地址&#xff1a;Welcome to Python.orgpycharm&#xff08;编译器&#xff09;下载地址&#xff1a;PyCharm: the Python IDE for Professional Developers by JetBrains一、python的下载与安装到官网后根据步骤下载安装包后&#xf…
阅读更多...
xgboost：分割查找：Weighted Quantile Sketch

xgboost：分割查找：Weighted Quantile Sketch

Weighted Quantile Sketch 专门处理流式和分布式加权数据集的一种分桶的方法 近似算法的一个重要步骤是提出候选分裂点。通常使用特征的百分位数来使候选数据均匀分布。形式上&#xff0c;设Dk(x1k,h1)&#xff0c;(x2k,h2)⋅⋅⋅(xnk,hn)D_k {(x_{1k}, h_1)&#xff0c;(x_…
阅读更多...
Redis持久化：RDB、AOF

Redis持久化：RDB、AOF

Redis持久化一. RDB(1) save(2) bgsave(3) 总结二. AOF(1) 重写优化(2) RDB和AOF的区别引入&#xff1a;Redis用内存存储数据&#xff0c;有数据丢失的问题&#xff1b; 一. RDB RDB&#xff08;Redis Database Bcakup file&#xff09;即Redis数据备份文件&#xff0c;或Red…
阅读更多...
如何用 Python采集 ＜豆某yin片＞并作词云图分析 ？

如何用 Python采集 ＜豆某yin片＞并作词云图分析 ？

嗨害大家好鸭&#xff01;我是小熊猫~ 总有那么一句银幕台词能打动人心 总有那么一幕名导名作念念不忘 不知道大家有多久没有放松一下了呢&#xff1f; 本次就来给大家采集一下某瓣电影并做词云分析 康康哪一部才是大家心中的经典呢&#xff1f; 最近又有哪一部可能会成为…
阅读更多...
拉链表详解

拉链表详解

目录 一、拉链表概念 二、拉链表对应的业务需求 三、代码实现 3.1 数据初始化&#xff1a; 3.2 创建ods层增量表&#xff1a; 3.3 创建dwd层拉链表 3.4 数据更新 &#xff0c;将数据日期为2023-3-4的日期添加到拉链表中 3.4.1 先追加数据到ods层表 3.4.2 更新dwd层表数据 …
阅读更多...
【SpringCloud】SpringCloud详解之Ribbon实战

【SpringCloud】SpringCloud详解之Ribbon实战

目录前言SpringCloud Ribbon 负载均衡一需求二.RestTemplate远程调用配置负载均衡(order服务内修改)三.Ribbon实现负载均衡的原理四.Ribbon负载均衡策略1.负载均衡种类2.配置负载均衡(order服务中配置)五.Ribbon的饥饿加载配置(在order服务配置)前言 微服务中比如用户服务部署…
阅读更多...
sklearn使用入门

sklearn使用入门

文章目录1.机器学习1.1 机器学习简介1.2 有监督学习(supervised learning)1.3 无监督学习(unsupervised learning)1.4 半监督学习2. 机器学习工具SKlearn2.1 sklearn2.2 sklearn常用模块2.2.1 分类2.2.2 回归2.2.3 聚类2.2.4 降维2.2.5 模型选择2.2.6 数据预处理2.3 sklearn使用…
阅读更多...
Android startActivityForResult()废弃了，代替方案案例

Android startActivityForResult()废弃了，代替方案案例

安卓项目compileSdk为32&#xff0c;在使用startActivityForResult()方法时发现Android studio提示此方法已经废弃了。 目前的代替方案案例。 // 确保 app 的 build.gradle中已经引入了androidx.appcompat:appcompat dependencies {implementation androidx.appcompat:appcomp…
阅读更多...
操作系统之进程管理---每天一点点（春招加油呀）--知识点回顾（自问自答版本总结）

操作系统之进程管理---每天一点点（春招加油呀）--知识点回顾（自问自答版本总结）

1.什么是进程&#xff1f;什么是线程&#xff1f;进程和线程的区别&#xff1f; 进程&#xff1a;资源分配和管理的基本单位 线程&#xff1a;程序执行的最小单位。 区别&#xff1a; 地址空间&#xff1a; 同一进程的所有线程共享本进程的地址空间&#xff0c;而不同的进程之间…
阅读更多...
仓库拣货标签电子价格标签办公电子标牌

仓库拣货标签电子价格标签办公电子标牌

数字货架标签尺寸&#xff1a;2.13英寸、2.9英寸、4.2英寸、7.5英寸、10.2英寸技术&#xff1a;2.4G MHz无线通信技术&#xff0c;电子墨水显示。刷新20&#xff0c;000个标签/1小时/AP。3-5年的寿命&#xff0c;电池可以快速更换。ESL管理系统工作原理&#xff1a;实时显示最新…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023