重点

童鞋们看网上讲解的时候一定要分清楚序列是从0开始还是从1开始，有些博主就是纯纯的转载文章，没有任何修改，把一篇错误的文章转来转去，误导了同学们。

所以我在这里提醒同学们一定要注意序列下标从什么开始的。

我的算法是根据王道考研总结出来的，并且主串、模式、next的下标都是从1开始的

1. 简单模式匹配算法

int search(String txt, String part){
	for(int i=0; i<txt.length-part.length; ++i){
		for(int j=0; j<M; j++){
			if(part[j] != txt[i+j]) break;
		}
		if(j == M) return i;
	}
	return -1;
}

2. 部分匹配值PM的算法（Move = j-1 + PM[j-1]）

1. 部分匹配值PM

模式（a b c a c）
‘a’的前缀为空，后缀为空，两者交集为空；
‘ab’的前缀为{a}，后缀为{b}，两者交集为空；
‘abc’的前缀为{a,ab}，后缀为{bc,c},两者交集为空；
'abca’的前缀为{a,ab,abc}，后缀{bca,ca,a}，两者交集为{a}；
‘abcac’的前缀为{a,ab,abc,abca}，后缀{bcac,cac,ac,c}，两者交集为空

2. 利用上述得到的部分匹配值PM完成匹配

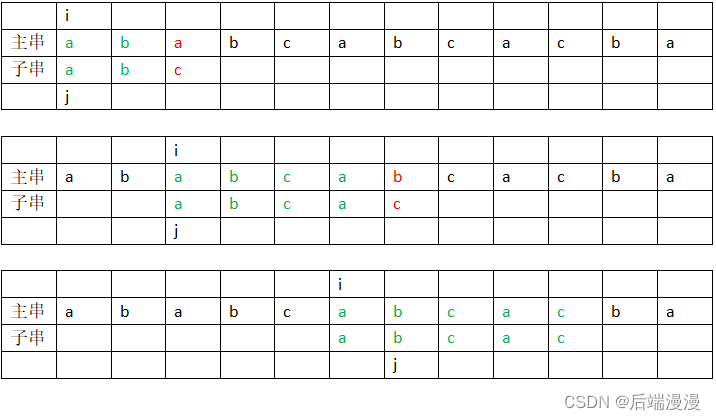
【第一趟匹配过程】
发现a与c不匹配，前两个字符是匹配的，查表可知，最后一个匹配字符b对应的部分匹配值为0，因此：移动位数=已匹配的字符数 - 对应的部分匹配值=2-0=2，所以将子串向后移动2位。j=1+PM
【第二趟匹配过程】
发现b与c不匹配，前四个字符是匹配的，查表可知，最后一个匹配字符a对应的部分匹配值为1，因此：移动位数=已匹配的字符数 - 对应的部分匹配值=4-1=3，所以将子串向后移动3位。j=1+PM
【第三趟匹配过程】
成功

3. 具体实例

3. 部分匹配值PM的两次改进（Move = j-next[j]）

已知：右移位数=已匹配的字符数 - 对应的部分匹配值，即为Move=（j-1）- PM[j-1]；

使用部分匹配值时，每当匹配失败，就去找它前一个元素的部分匹配值，这样使用起来有些不方便，所以将PM表右移一位，这样哪个元素匹配失败，直接看它自己的部分匹配值即可。

有时候为了让公式变得更加简洁，可以将next数组整体+1；

于是next数组就出来了

4. 快速得到next数组

1. 手动画图

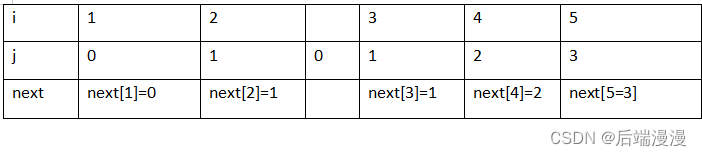
已知串 S= "babab ", 求 Next 数值序列（模式匹配）

• 首先第一位0，第二位1。这个是固定的。
• 第三位，字符串是“bab”，这时候“bab”的前缀有b，ba；后缀有ab，b，可以看出前后缀相等的最长的字符串只有b，因为b的长度是1，所以这里第三位的next值就是1。
• 第四位，字符串是“baba”，前缀是b,ba,bab；后缀是aba,ba,a。这里可以看出前后缀相等的最长的字符串是ba，长度是2，因此第四位的next值是2。
• 第五位，字符串是“babab”，前缀是b,ba,bab,baba；后缀是abab,bab,ab,b。这里可以看出前后缀相等的最长的字符串是bab，长度是3，因此第五位的next值是3.
• 因此综合起来next值就是0 1 1 2 3

2. 代码实现next数组

void get_next(String T,int next[]){
	int i=1,j=0;
	next[1]=0;
	while(i<T.length){
		if(j==0||T.ch[i]==T.ch[j]){
			++i,++j;
			next[i]=j;
		}
		else j=next[j];
	}
}

5. KMP匹配算法

int Index(SString S,SString T,int next[]){

	int i=1,j=1;
	while(i<=S.length&&j<=T.length){
		//相同的话就一直匹配		
		if(j==0||S.ch[i]==T.ch[j]){			
			++i;		
			++j;		
		}
		//不同的话就回溯
		else{	        	
			j=next[j];
		}
		
	}
	//找到了，(i-1)-(T.length-1)=i-T.length
	if（j>T.length） return i-T.length;		
	//没找到
	else return 0;
}