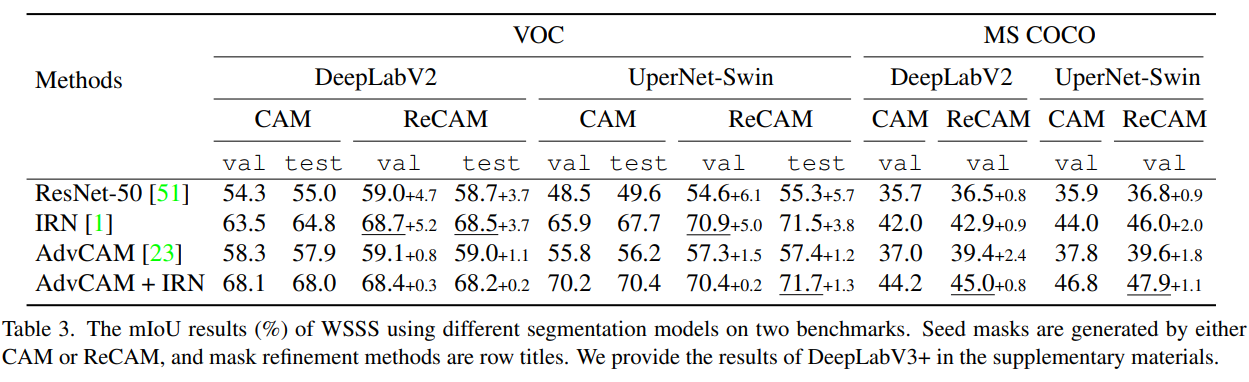
Weighted Quantile Sketch

专门处理流式和分布式加权数据集的一种分桶的方法

近似算法的一个重要步骤是提出候选分裂点。通常使用特征的百分位数来使候选数据均匀分布。形式上，设$D_k=(x_{1k},h_1)，(x_{2k},h_2)\cdot \cdot \cdot (x_{nk},h_n)$表示每个训练实例的第$k$个特征值和二阶梯度统计量。我们可以定义一个秩函数$rk:R\to [0,+\infty )$:
$$r_k(z)=\frac{1}{{\sum }_{(x,h)\in {\mathcal{D}}_k}h}\sum _{(x,h)\in {\mathcal{D}}_k,x<z}h,$$
表示在特征值$k$小于$z$的样本数的比例，目标找到候选划分点 { s k 1 , s k 2 , ⋯ s k l } , \{s_{k1},s_{k2},\cdots s_{kl}\}, {sk1​,sk2​,⋯skl​},：
$$|r_k(s_{k,j})-r_k(s_{k,j+1})|<ϵ,s_{k1}=\underset{i}{\min }{\mathbf{x}}_{ik},s_{kl}=\underset{i}{\max }{\mathbf{x}}_{ik}.$$
$ϵ$：近似因子，分成$1/ϵ$个候选点。每个数据点使用$h_i$加权。

加权的平方损失：
$$\sum _{i=1}^n\frac{1}{2}{h}_i(f_t({\mathbf{x}}_i)-g_i/h_i{)}^2+\Omega (f_t)+constant,$$
$gi/hi$：标签；

$h_i$：权重；

针对加权数据集的分位数算法，使用分布式加权分位数算法，该算法能够处理加权数据，并具有可证明的理论保证，可以处理大型数据集。总体思想是提出一种支持合并和修剪操作的数据结构，并证明每个操作都保持一定的精度水平。

要理解作者的加权分位数划分快速算法实现先要理解非加权的分位数划分算法：

GK算法¹：

GK算法是一种在具有确定性误差边界的高速数据流中计算近似分位数的快速算法。对于大小为N的数据流，其中N是预先未知的，算法将流划分为大小呈指数增长的子流。对于每个具有固定大小的子流，我们使用一种新的算法计算和维护一个多层次的summay。为了实现高速性能，该算法使用简单的分块合并和采样操作。总的来说，对于固定大小的流和任意大小的流，算法具有$O(Nlog(1/ϵ\ast log(ϵN))$的计算成本，如果$ϵ$是固定的，则每个元素的平均更新成本为$O(loglogN)$。

• 合并操作：结合两个summay带着误差${ϵ}_1$和${ϵ}_2$的结构，并且合并后的summay的近似误差是$max({ϵ}_1,{ϵ}_2)$。
• 剪枝操作：减少在summay的元素数量到$b+1$和改变近似误差从$ϵ$到$ϵ+\frac{1}{b}$

GK算法的产生要解决什么问题？

为了满足对数据近似分位点的频繁查询，考虑以下几种场景：

1. 固定不变的数据集
  2. 流式数据，数据长度不断增加
  3. 数据源分布存储，但数据长度固定
  4. 数据源分布存储+流式数据，数据长度不断增加

对于固定不变的数据集，排序后直接用二分法计算分位点，但是对于2、3、4，如果每次新增数据就重新排序，会带来很大的计算开销。GK算法就是用来解决这样的问题。

GK算法的具体步骤和实现²：

具体步骤在论文中²。

总体算法框架：

压缩算法：

xgboost的带权重样本的分位点近似算法

算法流程：

相关证明：
计算rank：
$$r_{\mathcal{D}}^{-}(y)=\sum _{(x,w)\in \mathcal{D},x<y}w$$

$$r_{\mathcal{D}}^{+}(y)=\sum _{(x,w)\in \mathcal{D},x\le y}w$$

计算权重：
$$\omega (\mathcal{D})=\sum _{(x,w)\in \mathcal{D}}w$$

定义四元组：
Q ( D ) = { S , r ~ D + , r ~ D − , ω ~ D } , Q({\mathcal D})=\{S,\tilde{r}_{\mathcal D}^{+},\tilde{r}_{\mathcal D}^{-},\tilde{\omega}_{\mathcal D}\}, Q(D)={S,r~D+​,r~D−​,ω~D​},
{ S , r ~ D + , r ~ D − , ω ~ D } , \{S,\tilde{r}_{\mathcal D}^{+},\tilde{r}_{\mathcal D}^{-},\tilde{\omega}_{\mathcal D}\}, {S,r~D+​,r~D−​,ω~D​},分别代表特征值、rank和权重；

其中的merge操作：

其中的prune

代码实现

///<The tuple in D
typedef struct D_tuple
{
	float x;
	float w;
}D_tuple_t;


///<The quintuple summary from set D
typedef struct Summary_Q
{
	std::vector<float> S;
	float r_positive;
	float r_negative;
	float w;
}Summary_Q_t;

^1345267

参考：

---

1. Zhang, Q., & Wang, W. (2007). A Fast Algorithm for Approximate Quantiles in High Speed Data Streams. 19th International Conference on Scientific and Statistical Database Management (SSDBM 2007). doi:10.1109/ssdbm.2007.27 ↩︎ ↩︎

2. Stream Algorithms: Order Statistics | paper cruncher (wordpress.com) ↩︎ ↩︎ ↩︎

3. ( GK Summay算法（ϵ−approximate ϕ−quantile）_gk算法_cyber19的博客-CSDN博客 ↩︎

4. [Stream Algorithms: Order Statistics | paper cruncher (wordpress.com)](https://titanssword.github.io/2018-07-26-GK.html) ↩︎

5. Greenwald, M., & Khanna, S. (2001). Space-efficient online computation of quantile summaries. ACM SIGMOD Record, 30(2), 58–66. doi:10.1145/376284.375670 ↩︎

6. XGBoost解读(2)–近似分割算法 • YXZF’s Blog ↩︎

7. xgboost之分位点算法 - Data Valley
   boost-v2/) ↩︎