spaf求最短路模板

只有当一个点的前驱结点更新了，该节点才会得到更新

因此只需要创建一个队列每一次加入距离被更新的结点

队列存的是待更新的节点——取出队列里的节点会更新它的后续节点

已经在队列的节点不需要重复入队，可以用st数组标记已入队节点

spfa算法步骤：

建立队列，队列初始只有节点1
取出队头节点x，取消该点标记，遍历x所有出边（x,y,z），若dist[y]>dist[x]+w，则更新最短路dist[y]=dist[x]+w，若y不在队列中，让y入队并标记
重复上述步骤，直到队列为空
注：dist[x]存1→x的最短路径长度 st[x]标记x节点是否在队列中

活动 - AcWing

题目：

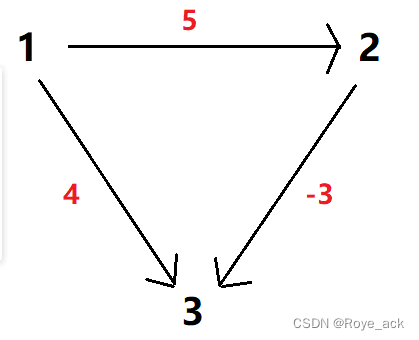
给定n个点m条边的带权有向图，图中可能存在重边和自环，边权可能为负数

请你求出 1 号点到 n 号点的最短距离，如果无法从 1 号点走到 n 号点，则输出 impossible。

数据保证不存在负权回路。

/*
    *道阻且长，行则将至*
    author:Roye_ack
*/
import java.util.*;
import java.io.*;
import java.math.*;
 
class Main
{
    static PrintWriter wt=new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));
    static int N=100010;
    static int n,m,idx;
    static int[] h=new int[N],e=new int[N],ne=new int[N],w=new int[N];
    static int[] dist=new int[N];
    static int[] st=new int[N];
    
    public static void add(int a,int b,int c)
    {
        e[idx]=b;w[idx]=c;ne[idx]=h[a];h[a]=idx++;
    }
    
    public static int spaf()
    {
        Queue<Integer> q=new LinkedList<>();
        q.offer(1);
        Arrays.fill(dist,0x3f3f3f3f);
        dist[1]=0;
        st[1]=1;
        
        while(!q.isEmpty())
        {
            var t=q.poll();
            st[t]=0;
            
            for(int i=h[t];i!=-1;i=ne[i])
            {
                int j=e[i];
                if(dist[j]>dist[t]+w[i])
                {
                    dist[j]=dist[t]+w[i];
                    if(st[j]==0) //如果当前队列里不存在该节点 则入队并标记
                    {
                        q.offer(j);
                        st[j]=1;
                    }
                }
            }
        }
        return dist[n];
    }
    
    public static void main(String[] args) throws IOException
    {
        n=rd.nextInt();
        m=rd.nextInt();
        
        Arrays.fill(h,-1);
        
        while(m-->0)
        {
            int a=rd.nextInt(),b=rd.nextInt(),c=rd.nextInt();
            add(a,b,c);
        }
        
        int res=spaf();
        if(res==0x3f3f3f3f) wt.print("impossible");
        else wt.print(res);
 
        wt.flush();
    }
    
    static class rd
    {
        static BufferedReader bf=new BufferedReader(new InputStreamReader(System.in));
        static StringTokenizer tk=new StringTokenizer("");
        
        static String nextLine() throws IOException
        {
            return bf.readLine();
        }
        
        static String next() throws IOException
        {
            while(!tk.hasMoreTokens()) tk=new StringTokenizer(bf.readLine());
            return tk.nextToken();
        }
        
        static int nextInt() throws IOException
        {
            return Integer.parseInt(next());
        }
        
        static double nextDouble() throws IOException
        {
            return Double.parseDouble(next());
        }
        
        static long nextLong() throws IOException
        {
            return Long.parseLong(next());
        }
        
        static BigInteger nextBig() throws IOException
        {
            BigInteger d=new BigInteger(rd.nextLine());
            return d;
        }
    }
}
 
class PII
{
    int x,y;
    PII(int x,int y)
    {
        this.x=x;
        this.y=y;
    }
}

852. spfa判断负环

活动 - AcWing

题目：

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环，边权可能为负数

请你判断图中是否存在负权回路

思路：

在spfa基础上添加一个cnt数组，cnt[x]存1→x经过的边数

边数cnt的更新方式：cnt[x]=cnt[t]+1（1到t的边数+1）

判断负环原理：

如果cnt[x]≥n，说明1~x至少经过了n+1个点，由抽屉原理可知至少两个点的编号一样
由于只有当dist[x]<dist[t]+w[i]才会更新cnt边数，因此w[i]必定是负数
综上可判断图中存在负环

/*
    *道阻且长，行则将至*
    author:Roye_ack
*/
import java.util.*;
import java.io.*;
import java.math.*;
 
class Main
{
    static PrintWriter wt=new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));
    static int N=100010;
    static int n,m,idx;
    static int[] h=new int[N],e=new int[N],ne=new int[N],w=new int[N];
    static int[] dist=new int[N],cnt=new int[N]; //cnt用于存边数
    static int[] st=new int[N];
    
    public static void add(int a,int b,int c)
    {
        e[idx]=b;w[idx]=c;ne[idx]=h[a];h[a]=idx++;
    }
    
    public static boolean spaf()
    {
        Queue<Integer> q=new LinkedList<>();
        //这里不用初始化dist数组为 正无穷/初始化的原因是：如果存在负环，那么dist不管初始化为多少，都会被更新
        
        for(int i=1;i<=n;i++) //该题是判断是否存在负环，并非判断是否存在从1开始的负环，因此需要将所有的点都加入队列中，更新周围的点
        {
            q.offer(i);
            st[i]=1;
        }
        
        while(!q.isEmpty())
        {
            var t=q.poll();
            st[t]=0;
            
            for(int i=h[t];i!=-1;i=ne[i])
            {
                int j=e[i];
                if(dist[j]>dist[t]+w[i])
                {
                    dist[j]=dist[t]+w[i];
                    cnt[j]=cnt[t]+1;
                    
                    if(cnt[j]>=n) return true;
                    
                    if(st[j]==0)
                    {
                        q.offer(j);
                        st[j]=1;
                    }
                }
            }
        }
        return false;
        
    }
    
    public static void main(String[] args) throws IOException
    {
        n=rd.nextInt();
        m=rd.nextInt();
        
        Arrays.fill(h,-1);
        
        while(m-->0)
        {
            int a=rd.nextInt(),b=rd.nextInt(),c=rd.nextInt();
            add(a,b,c);
        }
        
        if(spaf()) wt.print("Yes");
        else wt.print("No");
 
        wt.flush();
    }
    
    static class rd
    {
        static BufferedReader bf=new BufferedReader(new InputStreamReader(System.in));
        static StringTokenizer tk=new StringTokenizer("");
        
        static String nextLine() throws IOException
        {
            return bf.readLine();
        }
        
        static String next() throws IOException
        {
            while(!tk.hasMoreTokens()) tk=new StringTokenizer(bf.readLine());
            return tk.nextToken();
        }
        
        static int nextInt() throws IOException
        {
            return Integer.parseInt(next());
        }
        
        static double nextDouble() throws IOException
        {
            return Double.parseDouble(next());
        }
        
        static long nextLong() throws IOException
        {
            return Long.parseLong(next());
        }
        
        static BigInteger nextBig() throws IOException
        {
            BigInteger d=new BigInteger(rd.nextLine());
            return d;
        }
    }
}
 
class PII
{
    int x,y;
    PII(int x,int y)
    {
        this.x=x;
        this.y=y;
    }
}

341. 最优贸易 - spfa + 双向建图

活动 - AcWing

题目：

n个城市m条边，1代表x到y单向通道，2代表x到y的双向通道

每个城市都有一个商品的价格，一人从1号点出发，在某个城市买一个商品

在另一个城市卖出，该交易只进行一次

问最大赚取的差价为多少？

思路：

为何不能用dijkstra算法？

如果当前 dmin[i] 最小的点是 5，那么有可能存在边 5-> 6, 6-> 7, 7-> 5，假设当前 dmin[5] = 10，则有可能存在 6 的价格是11，但 7 的价格是3，那么 dmin[5] 的值就应该被更新成3，因此当前最小值也不一定是最终最小值，所以dijkstra算法并不适用，我们只能采用 spfa 算法

dijkstra算法的特性保证后面出现的点都比前面出现的差，不能及时更新最小值

思路总体就是：1~i正向取最小 n~i反向取最大枚举所有点作为中间点i 求出差值的最大值

从 1 走到 i 的过程中，买入水晶球的最低价格 dmin[i]；
从 i 走到 n 的过程中，卖出水晶球的最高价格 dmax[i]；

然后枚举每个城市作为买卖的中间城市，求出 dmax[i] - dmin[i] 的最大值

为什么不能正向求出i号点到n号点求出最大价格？

因为并不是所有点到终点都是可达的，必须保证从1号点走到i号点时，i号点一定能走到n号点

/*
    *道阻且长，行则将至*
    author:Roye_ack
*/
import java.util.*;
import java.io.*;
import java.math.*;
 
class Main
{
    static PrintWriter wt=new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));
    static int N=100010,M=5*N;
    static int n,m,idx;
    static int[] h=new int[N],rh=new int[N],e=new int[M],ne=new int[M];
    static int[] w=new int[N];
    static int[] st=new int[N];
    static int[] dmin=new int[N],dmax=new int[N];
    
    public static void add(int[]h,int a,int b)
    {
        e[idx]=b;ne[idx]=h[a];h[a]=idx++;
    }
    
    public static void spfa(int[] d,int start,int[] h,boolean flag)
    {
        Queue<Integer> q=new LinkedList<>();
        
        if(flag) Arrays.fill(d,0x3f3f3f3f);
        
        q.offer(start);
        d[start]=w[start];
        st[start]=1;
        
        while(!q.isEmpty())
        {
            var t=q.poll();
            st[t]=0;
            
            for(int i=h[t];i!=-1;i=ne[i])
            {
                int j=e[i];
                if(flag&&d[j]>Math.min(d[t],w[j])||!flag&&d[j]<Math.max(d[t],w[j]))
                {
                    if(flag) d[j]=Math.min(d[t],w[j]);
                    else d[j]=Math.max(d[t],w[j]);
                    
                    if(st[j]==0)
                    {
                        st[j]=1;
                        q.offer(j);
                    }
                }
            }
        }
    }
    
    public static void main(String[] args) throws IOException
    {
        n=rd.nextInt();
        m=rd.nextInt();
        
        Arrays.fill(h,-1);
        Arrays.fill(rh,-1);
        
        for(int i=1;i<=n;i++) w[i]=rd.nextInt();
        
        while(m-->0)
        {
            int a=rd.nextInt(),b=rd.nextInt(),c=rd.nextInt();
            add(h,a,b); //便于计算1~i点
            add(rh,b,a); //便于计算n~i点
            if(c==2) 
            {
                add(h,b,a);
                add(rh,a,b);
            }
        }
        
        spfa(dmin,1,h,true);
        spfa(dmax,n,rh,false);
 
        int res=0;
        for(int i=1;i<=n;i++) res=Math.max(res,dmax[i]-dmin[i]);
        wt.print(res);
        wt.flush();
    }
    
    static class rd
    {
        static BufferedReader bf=new BufferedReader(new InputStreamReader(System.in));
        static StringTokenizer tk=new StringTokenizer("");
        
        static String nextLine() throws IOException
        {
            return bf.readLine();
        }
        
        static String next() throws IOException
        {
            while(!tk.hasMoreTokens()) tk=new StringTokenizer(bf.readLine());
            return tk.nextToken();
        }
        
        static int nextInt() throws IOException
        {
            return Integer.parseInt(next());
        }
        
        static double nextDouble() throws IOException
        {
            return Double.parseDouble(next());
        }
        
        static long nextLong() throws IOException
        {
            return Long.parseLong(next());
        }
        
        static BigInteger nextBig() throws IOException
        {
            BigInteger d=new BigInteger(rd.nextLine());
            return d;
        }
    }
}
 
class PII
{
    int x,y;
    PII(int x,int y)
    {
        this.x=x;
        this.y=y;
    }
}