FMCW信号

调频连续波(frequency modulated continuous wave，FMCW)顾名思义，就是对信号的频率进行线性调制的信号。

从时域上看，对频率的调制，就像一把连续的锯齿波。其中每一个锯齿叫做一个chirp，其持续的时间叫做chirp的周期（chirp period 或 chirp repetition time）；在实际使用中，我们将chirp合并成一帧（frame）进行发送，从而得到物体的速度（或多普勒频偏）信息，是为FMCW信号。

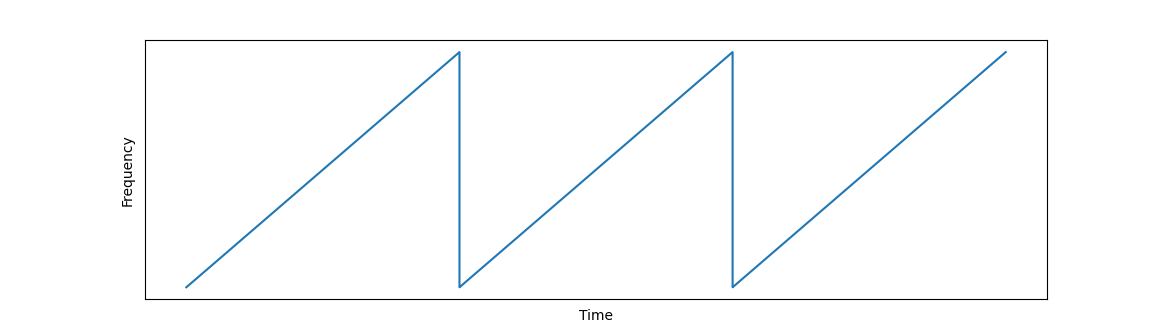
请添加图片描述

我们定义扫频带宽与chirp周期的比值为系数K，也即锯齿波的斜率（slope）。
$\frac{扫频带宽}{chirp周期}= \frac{扫频终止频率-扫频起始频率}{chirp周期}$

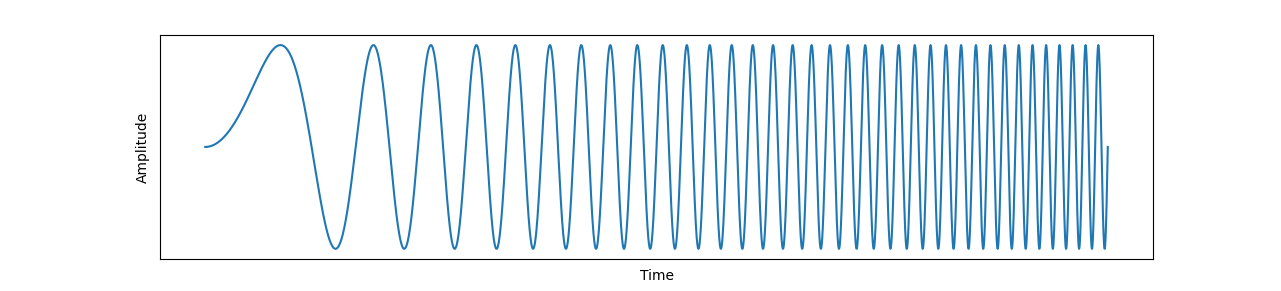
如果从时域上看此时信号幅度的变化，可以发现随着时间的推移，对应正弦波的频率会越来越高，即呈现越来越密的特点。
请添加图片描述

中频信号

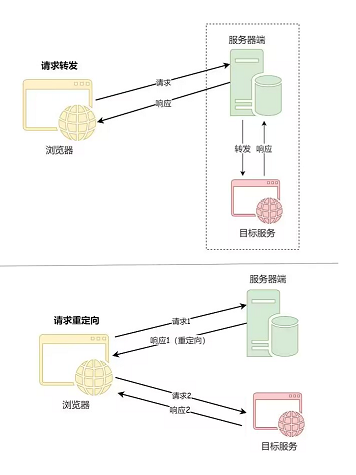
我们采用的IF信号就是指接收的回波信号与原始信号进行混频后，再过低通滤波器得到的低中频信号（或差拍信号，beat signal）。用一个简图来表示就是：

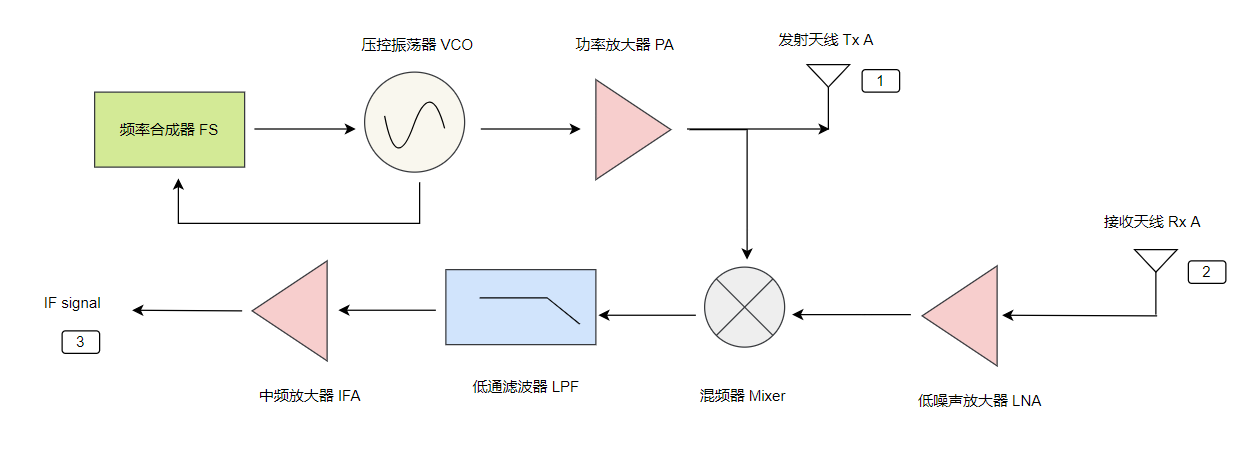
在这里插入图片描述

我们只关注1处发射信号、2处接收信号和3处IF信号的表达形式即可。

1处发射信号

由于发送信号为FMCW信号，取其中一个chirp，我们知道相位对时间的导数为角频率（再除以 $\pi$ 即频率），如下：
$\frac{1}{2\pi}\frac{d \phi}{dt} = f_o+Kt$
于是，我们对上式两边积分，就有：
$\phi = 2\pi( f_ot + \frac{1}{2}Kt^2)+\phi_o = 2\pi f_ot + \pi Kt^2+\phi_0$
所以1处发射信号的形式为：
$x_{\tiny{T}x}(t) = A \sin(2 \pi f_ot +\pi Kt^2+\phi_0)$

注意上式为发送的实信号形式（在物理世界中传输的都是实信号），将其转换为复信号（在信号处理中这可由希尔伯特变换实现），即

$x_r = Ae^{j(2 \pi f_ot +\pi Kt^2+\phi_0)}$

其中，K为斜率， $\phi_o$ 为信号的初始相位， $f_0$ 为中心频率：

$f_o =\frac{扫频起始频率+扫频结束频率}{2}$

2处接收信号

在这里插入图片描述

发送的信号在遇到目标（Target）后就会反射，从而产生2处接收天线的回波信号，假设这个时延为 $\tau$ ，衰减系数为 $a$ ，则

$x_{\tiny{R}x}(t) = a x_{\tiny{T}x}(t-\tau) = A^{\prime} \sin[2 \pi f_o(t-\tau) +\pi K(t-\tau)^2+\phi_0] \\ =A\sin[\pi K t^2 +2\pi (f_o - K \tau)t+\pi K \tau^2-2 \pi f_o \tau + \phi_0]$

3处IF信号

根据三角公式中的积化和差公式，即：
$\sin(\alpha) \sin(\beta) = \frac{1}{2}[\cos(\alpha - \beta) - \cos(\alpha + \beta) ]$

于是我们混频后的信号为：
$x_{\tiny{T}x}(t) \times x_{\tiny{R}x}(t) =\frac{1}{2}AA^{\prime}[\cos(2\pi K\tau t+2\pi f_o \tau-\pi K \tau^2 ) \\- \cos(2\pi(2 f_o-K \tau)t+...)]$
经过低通滤波器后，结果中的和式将作为高频成分被滤除，而只留下差式中低频的成分，我们再将这个差信号通过中频放大器放大，最终将得到3处的中频信号，即：

$x_{\tiny{IF}}(t) = A^{\prime \prime} \cos(2\pi K\tau t+2\pi f_o \tau-\pi K \tau^2 )$

我们再对上面的参数有一个感性的认识：由于电磁波以光速运动，在前方1m处的目标其时延 $\tau$ 的量级大致在 $10^{-8}$ ， $f_0$ 对于毫米波雷达在 $10^9$ 量级，而一般的 K 大概是1GHz除以0.1ms级别，即 $10^{-13}$ 级。比较两个附加相位：
$f_o \tau \approx 10 \ \ \ K\tau ^2 \approx 10^{-3}$
所以最后一项的附加相位几乎可以忽略不计，即一般将中频信号的形式写为：