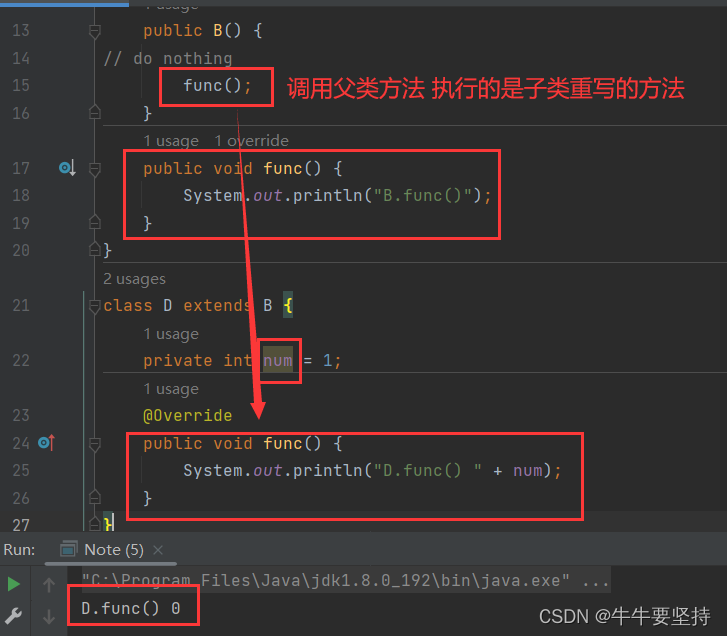
弗洛伊德算法-Floyd(Floyd-Warshall)-求多源最短路径,求传递闭包
Floyd算法又称为插点法,是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法,
与Dijkstra算法类似。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。
为什么要求传递闭包?
因为:一个有n个顶点的有向图的传递闭包为:有向图中的初始路径可达情况可以参见其邻接矩阵A,
邻接矩阵中A[i,j]表示i到j是否直接可达,若直接可达,则A[i,j]记为1,否则记为0;两个有向图
中i到j有路径表示从i点开始经过其他点(或者不经过其他点)能够到达j点,如果i到j有路径,
则将T[i,j]设置为1,否则设置为0;有向图的传递闭包表示从邻接矩阵A出发,求的所有节点
间的路径可达情况,该矩阵就为所要求的传递闭包矩阵
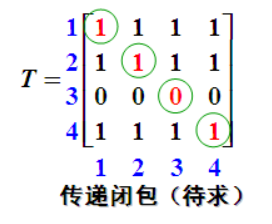
warshall传递闭包算法的目的:就是由邻接矩阵出发,进行探索求出最终的传递闭包
(i是行,j是列)
算法过程:
(1)i=1时,第一列有A[4,1]=1,将第四行元素分别与第一行对应元素进行
逻辑加(或运算):
0 1 0 0
0 0 0 1
0 0 0 0
1 1 1 0
(2)i=2时,第二列有A[1,2]=1,A[4,2]=1,将第一行元素和第四行元素分别与第二行
对应元素进行逻辑加:
0 1 0 1
0 0 0 1
0 0 0 0
1 1 1 1
(3)i=3时,第三列有A[4,3]=1,将第四行元素分别与第三行对应元素进行逻辑加:
0 1 0 1
0 0 0 1
0 0 0 0
1 1 1 1
(4)i=4时,第四列有A[1,4]=1,A[2,4]=1,A[4,4]=1,将第一行元素、第二行
元素和第四行元素分别与第四行对应元素进行逻辑加:
1 1 1 1
1 1 1 1
0 0 0 0
1 1 1 1
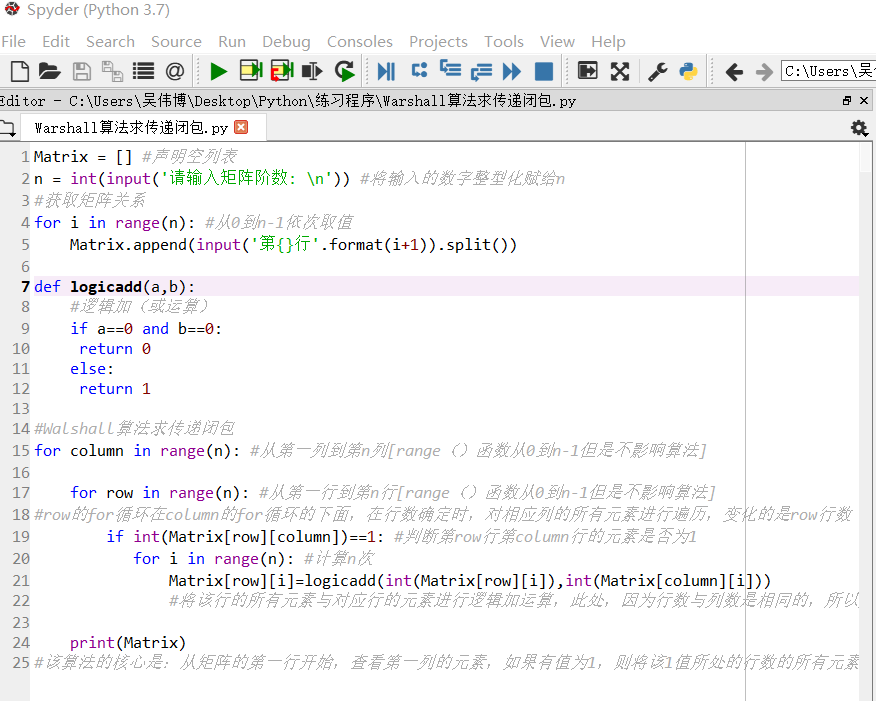
Python核心代码:
Matrix = [] #声明空矩阵
n = int(input('请输入矩阵阶数: \n')) #将输入的数字整型化赋给n
#获取矩阵关系
for i in range(n): #从0到n-1依次取值
Matrix.append(input('第{}行'.format(i+1)).split())
def logicadd(a,b):
#逻辑加(或运算)
if a==0 and b==0:
return 0
else:
return 1
#Walshall算法求传递闭包
for column in range(n): #从第一列到第n列[range()函数从0到n-1但是不影响算法]
for row in range(n): #从第一行到第n行[range()函数从0到n-1但是不影响算法]
#row的for循环在column的for循环的下面,在行数确定时,对相应列的所有元素进行遍历,变化的是row行数
if int(Matrix[row][column])==1: #判断第row行第column行的元素是否为1
for i in range(n): #计算n次
Matrix[row][i]=logicadd(int(Matrix[row][i]),int(Matrix[column][i]))
#将该行的所有元素与对应行的元素进行逻辑加运算,此处,因为行数与列数是相同的,所以用column固定值表示
print(Matrix)
#该算法的核心是:从矩阵的第一行开始,查看第一列的元素,如果有值为1,则将该1值所处的行数的所有元素与第一行的对应元素进行逻辑加运算;依次计算......
另外一种思想:
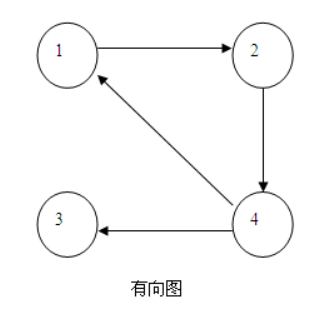
如果知道点数,知道边数以及边的方向,该如何求出传递闭包?
请思考:k阶应该在最里层,还是最外层,为什么? 如何体现 i->k 和 k->j的与?
map()函数的格式是:
map(function,iterable,...)
第一个参数接受一个函数名,后面的参数接受一个或多个可迭代的序列,返回的是一个集合。
把函数依次作用在list中的每一个元素上,得到一个新的list并返回。
用法:zeros(shape, dtype=float, order='C')
返回:返回来一个给定形状和类型的用0填充的数组;
shape:形状
dtype:数据类型,可选参数,默认numpy.float64
order:可选参数,c代表与c语言类似,行优先;F代表列优先
range(10)表示: range(0, 10)
python编程代码如下:
import numpy as np
def Warshall(A,n):
for k in range(n):
for i in range(n):
for j in range(n):
A[i][j] = A[i][j] or (A[i][k] and A[k][j]) #k-1阶的时候,A[i,j]如果是1,那么就似乎A[i,j] = A[i,j],如果A[i,j]是0,再看 A[i,j] = A[i,k] and A[k,j]
return A #i相当于1,k相当于2,j相当于3;若有从1到3的直接路径,则覆盖。若只有从1到2再到3的间接路径,则取后面的间接路径,间接路径成立的条件是从1到2和从2到3都成立,所以是and
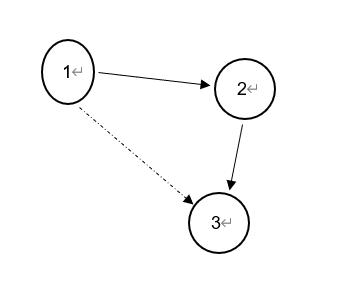
n,m=map(int,input("请输入点数n和边数m:").split()) #将点数和边数整型化后赋给n,m
A=np.zeros((n,n),dtype=np.int32)
for i in range(0,m): #同range(m)
a,b=map(int,input("请输入有向边的顶点a->b:").split()) #将有向边的顶点数字整型化后赋给a,b
A[a-1][b-1]=1
print("邻接矩阵为: \n",A)
print("最终的传递闭包为: \n",Warshall(A,n))