『OPEN3D』点云表面重建

news2024/11/18 17:23:41

目录

1 点云法线一致性估计

2 点云的表面重建

1 Alpha shapes reconstruction

2 Ball pivoting reconstruction

3 poisson surface reconstruction

1 点云法线一致性估计

  在点云处理的章节中已经介绍使用estimate_normals来生成点云的发现信息，但该方法通过拟合局部3D点来生成法线信息，因此生成的法线朝向一致性不够好。此处使用最小生成树来传播法线的方向，提高朝向的一致性。该方法为orient_normals_consistent_tangent_plane

import numpy as np
import open3d as o3d
import copy

if __name__ == '__main__':
    ply_point_cloud = o3d.data.PLYPointCloud()
    pcd: o3d.geometry.PointCloud = o3d.io.read_point_cloud(ply_point_cloud.path)
    pcd = pcd.voxel_down_sample(voxel_size=0.06)
    # pcd = gt_mesh.sample_points_poisson_disk(5000)
    # invalidate existing normals
    # 使得原有的法线信息失效
    pcd.normals = o3d.utility.Vector3dVector(np.zeros((1, 3)))

    pcd.estimate_normals()
    # o3d.visualization.draw_geometries([pcd], point_show_normal=True)

    pcd_spanning_tree: o3d.geometry.PointCloud = copy.deepcopy(pcd)

    # 参数K用于构造用于传播法线方向的黎曼图的k个最近邻数。
    pcd_spanning_tree.orient_normals_consistent_tangent_plane(k=300)
    pcd_spanning_tree.translate([4, 0, 0])
    o3d.visualization.draw_geometries([pcd_spanning_tree, pcd], point_show_normal=True)

 可以看到经过法线一致性调整后，法线朝向的一致性变得统一。

2 点云的表面重建

之前我们已经介绍了点云（point cloud）和面片（mesh）的内容，并且可以将mesh通过采样的方法得到点云信息，但是如何将稀疏的无结构点云重新生成表面mesh呢? 这就涉及到点云的表面重建的内容了。

        在open3d中，为我们提供了如下几种的表面重建方法：

  • Alpha shapes [Edelsbrunner1983]

  • Ball pivoting [Bernardini1999]

  • Poisson surface reconstruction [Kazhdan2006]

1 Alpha shapes reconstruction

 alpha shapes 实际上是一种点云的边界提取算法，如下图所示：

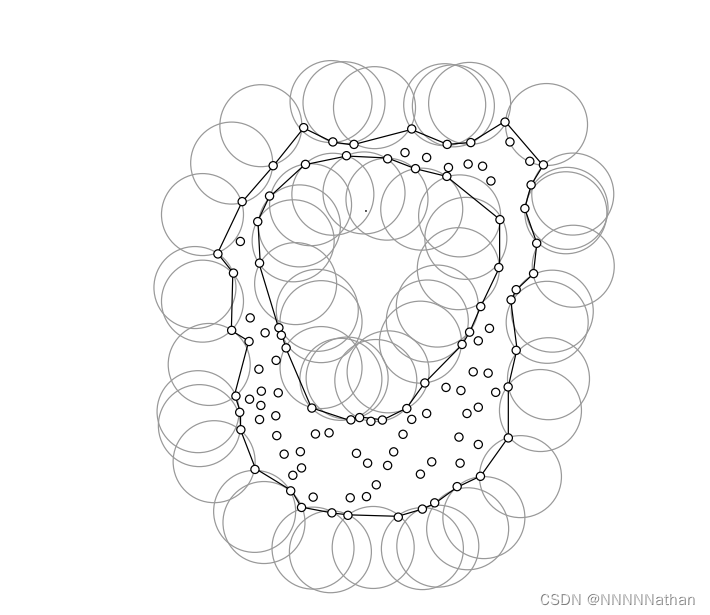
 选取半径为alpha大小的圆，并将此圆在空间的无序点云上进行滚动，然后绘制出轮廓线，该轮廓线就是点云的表面信息，如果alpha足够大，可以将该发放看做是求取点云的convex hull（凸包计算）。详细的解析可以看斯坦福的报告 。

代码示例：

import copy

import open3d as o3d

if __name__ == "__main__":
    bunny = o3d.data.BunnyMesh()
    mesh = o3d.io.read_triangle_mesh(bunny.path)
    mesh.compute_vertex_normals()

    # 对mesh进行采样，得到点云
    pcd = mesh.sample_points_poisson_disk(850)
    print("Displaying input pointcloud ...")
    o3d.visualization.draw_geometries([pcd])

    # 设置alpha shapes中的参数alpha

    alpha = 0.02
    mesh_list = [pcd]
    for index in range(1, 4):
        print(f"alpha={alpha:.3f}")
        print('Running alpha shapes surface reconstruction ...')
        alpha = alpha * index
        tetra_mesh, pt_map = o3d.geometry.TetraMesh.create_from_point_cloud(pcd)

        mesh: o3d.geometry.TriangleMesh = o3d.geometry.TriangleMesh.create_from_point_cloud_alpha_shape(
            pcd, alpha)
        mesh.compute_triangle_normals(normalized=True)
        mesh = mesh.translate([0.2 * index, 0, 0])
        mesh_list.append(copy.deepcopy(mesh))
        del mesh

    print("Displaying reconstructed mesh ...")
    # 显示时，mesh_show_back_face=True ： mesh内部视角也显示mesh面片
    o3d.visualization.draw_geometries(mesh_list, mesh_show_back_face=True)

2 Ball pivoting reconstruction

        Ball pivoting算法的实现思路与alpha shapes接近；想象一下, 一个给定半径大小的球体朝点云扔去，如果球体击中任意三个点且没有重中穿过，则该三个点创建一个triangles mesh；然后该算法以现有的这个triangles mesh的边沿开始进行周围的迭代，当击中另外三个点没有穿过时，创建另一个三角形。

import open3d as o3d

if __name__ == "__main__":
    bunny = o3d.data.BunnyMesh()
    gt_mesh = o3d.io.read_triangle_mesh(bunny.path)
    gt_mesh.compute_vertex_normals()

    pcd = gt_mesh.sample_points_poisson_disk(3000)
    print("Displaying input pointcloud ...")
    # o3d.visualization.draw_geometries([pcd])

    radii = [0.005, 0.01, 0.02, 0.04]
    print('Running ball pivoting surface reconstruction ...')
    # pcd中需要包含法线信息
    rec_mesh: o3d.geometry.TriangleMesh = o3d.geometry.TriangleMesh.create_from_point_cloud_ball_pivoting(
        pcd, o3d.utility.DoubleVector(radii))
    print("Displaying reconstructed mesh ...")

    o3d.visualization.draw_geometries([rec_mesh, pcd])

3 poisson surface reconstruction

 其中上面的点为点云的信息，mesh根据点云的信息进行生成

3 poisson surface reconstruction

        poisson surface reconstruction解决正则优化问题来生成更加平滑的表面信息，基于此，而上面提及的重建算法直接使用point cloud不加以修改的作为mesh的顶点（vertice）。

        open3d实现该方法通过create_from_point_cloud_poisson，实际时对GitHub - mkazhdan/PoissonRecon: Poisson Surface Reconstruction的封装实现。该算法的一个重要参数时depth，用于控制octree的深度；该参数可以控制生成triangle mesh的精细程度。越大的depth，生成的mesh拥有更多的细节。

create_from_point_cloud_poisson的参数
pcd  包含法线信息的待重建点云
depth

(int ，可选参数，默认=8) 曲面重建树的最大深度，在深度D处运行对应于分辨率不大于2^D*2^D*2^D的网格上进行求解。注：由于重建时根据采样密度调整OCTtree，因此此处指定的重建深度只是一个上限。

width（float ，可选参数，默认=0）指定最细级别的八叉树单元格的目标宽度；如果指定了深度，则此参数忽略。
scale（float，可选，默认值=1.1）指定用于重建的立方体直径与样本边界立方体直径之间的比率。
linear_fit（bool，可选，默认值=False）如果为true，重建时将使用线性插值来估计iso顶点的位置
n_threads（int，可选，默认值=-1）用于重建的线程数，设置为-1表示自动选择
import open3d as o3d
import numpy as np

if __name__ == "__main__":
    eagle = o3d.data.EaglePointCloud()
    pcd: o3d.geometry.PointCloud = o3d.io.read_point_cloud(eagle.path)
    R = pcd.get_rotation_matrix_from_xyz((np.pi, -np.pi / 4, 0))
    pcd.rotate(R, center=(0, 0, 0))
    pcd = pcd.voxel_down_sample(voxel_size=0.08)
    print('Displaying input pointcloud ...')
    # o3d.visualization.draw_geometries([pcd])

    print('Running Poisson surface reconstruction ...')
    mesh, densities = o3d.geometry.TriangleMesh.create_from_point_cloud_poisson(
        pcd, depth=9)
    print('Displaying reconstructed mesh ...')

    pcd = pcd.translate([10, 0, 0])
    o3d.visualization.draw_geometries([mesh, pcd])

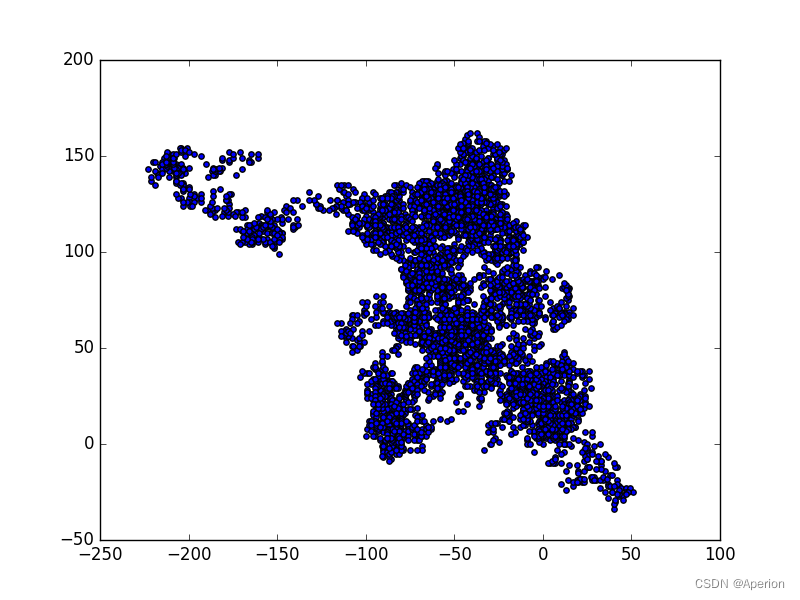
        Poisson surface reconstruction(泊松表面重建)也会在点云密度较低的地方创建mesh，甚至会向外延伸到其他区域,如下图底部区域所示；因此create_from_point_cloud_poisson函数的第二个返回值（densities）代表了每一个顶点的密度信息；低密度代表着该顶点（vertex）仅从一小部分的输入点云中生成。

       可以根据返回的密度信息来删除低密度区域的顶点（vertices）和mesh，这里使用numpy.quantile来删除出小于X分位数的密度值的顶点（vertices）和mesh。

import copy

import open3d as o3d
import numpy as np
import matplotlib.pyplot as plt

if __name__ == "__main__":
    eagle = o3d.data.EaglePointCloud()
    pcd: o3d.geometry.PointCloud = o3d.io.read_point_cloud(eagle.path)
    R = pcd.get_rotation_matrix_from_xyz((np.pi, -np.pi / 4, 0))
    pcd.rotate(R, center=(0, 0, 0))
    # pcd = pcd.voxel_down_sample(voxel_size=0.08)
    print('Displaying input pointcloud ...')
    # o3d.visualization.draw_geometries([pcd])

    print('Running Poisson surface reconstruction ...')
    mesh, densities = o3d.geometry.TriangleMesh.create_from_point_cloud_poisson(
        pcd, depth=9)
    print('Displaying reconstructed mesh ...')

    mesh = mesh.translate([5, 0, 0])
    o3d.visualization.draw_geometries([mesh, pcd], mesh_show_back_face=True)

    # 密度的cmap
    print('visualize densities')
    densities = np.asarray(densities)
    density_colors = plt.get_cmap('plasma')(
        (densities - densities.min()) / (densities.max() - densities.min()))
    density_colors = density_colors[:, :3]
    density_mesh = o3d.geometry.TriangleMesh()
    density_mesh.vertices = mesh.vertices
    density_mesh.triangles = mesh.triangles
    density_mesh.triangle_normals = mesh.triangle_normals
    density_mesh.vertex_colors = o3d.utility.Vector3dVector(density_colors)
    o3d.visualization.draw_geometries([density_mesh])
    density_mesh.translate([5, 0, 0])

    # 删除分位数小于0.005的顶点和mesh
    print('remove low density vertices')
    vertices_to_remove = densities < np.quantile(densities, 0.005)
    mesh_remove:o3d.geometry.PointCloud = copy.deepcopy(mesh)
    mesh_remove.remove_vertices_by_mask(vertices_to_remove)
    mesh_removed = mesh_remove.translate([10, 0, 0])
    print(mesh_removed)
    o3d.visualization.draw_geometries([mesh_removed, density_mesh, mesh, pcd])

上面结果图片中，最左边为原始的点云数据，其次时poisson重建的结果，其次时poisson重建的密度信息，最后时删除X分位后得到的重建结果。 可以看到删除低密度区域的顶点和mesh信息后，mesh结果展示没有了之前底部的多余信息。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/388842.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

业务流程测试

业务流程测试

用例设计主要问题主要问题存在于&#xff1a;1、测试点分析&#xff1a;逻辑性不强对于整个页面功能划分不清晰&#xff1b;不同测试点归类不清晰&#xff1b;不能形成相对固定的套路&#xff0c;书写耗费大量时间...2、测试用例&#xff1a;关于&#xff0c;要细致到什么程度&…
阅读更多...
一个供参考的计算机的学习路线

一个供参考的计算机的学习路线

本文是介绍如何成为一个Geek&#xff0c;一个真正的计算机高手。 适合有成为IT领域技术大牛的人参考。 写给大一新生和所有向深耕IT领域的人&#xff0c;避免走一些弯路。 仅代表个人想法&#xff0c;供批判性参考。 第一门入门的必备功课-语法与算法 什么是计算机&#xff1f…
阅读更多...
力扣sql简单篇练习(二十二)

力扣sql简单篇练习(二十二)

力扣sql简单篇练习(二十二) 1 上月播放的儿童适宜电影 1.1 题目内容 1.1.1 基本题目信息 1.1.2 示例输入输出 a 示例输入 b 示例输出 1.2 示例sql语句 # Write your MySQL query statement belowSELECT titleFROM ContentWHERE kids_contentY AND content_typeMoviesAND c…
阅读更多...
MYSQL性能分析,Explain

MYSQL性能分析,Explain

文章目录一、MYSQL常见瓶颈二、ExplainExplain是什么一、MYSQL常见瓶颈 CPU&#xff1a; CPU饱和IO&#xff1a;磁盘IO速度过慢。服务器的硬件性能瓶颈。 二、Explain Explain是什么 使用explain关键字可以模拟优化器执行sql查询语句&#xff0c;从而知道mysql如何处理你的…
阅读更多...
Python 随机漫步

Python 随机漫步

目录 1. 创建 RandomWalk 类 2. 选择方向 3. 绘制随机漫步图 4. 总结 本篇博客将使用 Python 来生成随机漫步数据&#xff0c;在使用 Matplotlib 以引人注目的方式将这些数据呈现出来。 随机漫步 是这样行走得到的路径&#xff1a;每次行走都是完全随机的、没有明确…
阅读更多...
跨域问题以及Ajax和Axios的区别

跨域问题以及Ajax和Axios的区别

文章目录1. 同源策略2. 同源策略案例3. 什么是跨域4. 跨域解决方法4.1 Ajax的jsonp4.2 CORS方式4.3 Nginx 反向代理5. Axios 和 Ajax 的区别6. Axios 和 Ajax 的区别及优缺点6.1 Ajax&#xff1a;6.1.1 什么是Ajax6.1.2 Ajax的原理6.1.3 核心对象6.1.4 Ajax优缺点6.1.4.1 优点&…
阅读更多...
大白话+画图 从源码角度一步步搞懂ArrayList和LinkedList的使用

大白话+画图 从源码角度一步步搞懂ArrayList和LinkedList的使用

1.说说ArrayList 1.基本原理 ArrayList&#xff0c;原理就是底层基于数组来实现。 01.基本原理&#xff1a; 数组的长度是固定的&#xff0c;java里面数组都是定长数组&#xff0c;比如数组大小设置为100&#xff0c;此时你不停的往ArrayList里面塞入这个数据&#xff0c;此…
阅读更多...
Warshall算法求传递闭包及Python编程的实现

Warshall算法求传递闭包及Python编程的实现

弗洛伊德算法-Floyd(Floyd-Warshall)-求多源最短路径&#xff0c;求传递闭包 Floyd算法又称为插点法&#xff0c;是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法&#xff0c; 与Dijkstra算法类似。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大…
阅读更多...
minikube搭建Kubernetes环境

minikube搭建Kubernetes环境

前言 Kubernetes 一般都运行在大规模的计算集群上&#xff0c;管理很严格&#xff0c;Kubernetes 充分考虑到了这方面的需求&#xff0c;提供了一些快速搭建 Kubernetes 环境的工具。 minikube 它是一个“迷你”版本的 Kubernetes&#xff0c;自从 2016 年发布以来一直在积极地…
阅读更多...
Lesson 8.1 决策树的核心思想与建模流程

Lesson 8.1 决策树的核心思想与建模流程

文章目录一、借助逻辑回归构建决策树1. 决策树实例2. 决策树知识补充2.1 决策树简单构建2.2 决策树的分类过程2.3 决策树模型本质2.4 决策树的树生长过程2.5 树模型的基本结构二、决策树的分类与流派1. ID3(Iterative Dichotomiser 3) 、C4.5、C5.0 决策树2. CART 决策树3. CHA…
阅读更多...
minio安装配置和使用（一）

minio安装配置和使用（一）

minio官网https://www.minio.org.cn 从官网获得安装文件。官网提供了Binary、RPM、DEB三种方式安装minio。 Binary方式我在我的测试环境中没有测试通过&#xff0c;按官网方式下载执行会报错如下&#xff1a; 查了下这个错误提示&#xff0c;似乎跟内存有关。 改用RPM方式安…
阅读更多...
HCIP第一个实验

HCIP第一个实验

实验要求与实验拓扑子网划分分析将骨干链路看成一个整体&#xff0c;路由器后的2个环回地址先看成一个&#xff0c;最后再进行拆分。计算得出&#xff0c;一共需要划分为6个子网段&#xff0c;取三位。再将每一条网段&#xff0c;按照题目要求进行划分最后完成子网划分。子网划…
阅读更多...
进行嵌入式C语言编程调试的通用办法

进行嵌入式C语言编程调试的通用办法

总结了一下调试我们嵌入式C程序的一些基本的办法和思想&#xff0c;供大家学习参考&#xff1a; 打印日志&#xff1a;在代码中添加打印语句&#xff0c;输出变量值、函数调用等信息&#xff0c;以便在程序运行时观察程序执行情况。 断点调试&#xff1a;在代码中添加断点&…
阅读更多...
【编程实践】用 go 语言实现 B+ 树

【编程实践】用 go 语言实现 B+ 树

文章目录 用 go 语言实现 B+ 树定义 B+ 树的结构B+ 树的插入操作函数B+ 树的查找小结用 go 语言实现 B+ 树 B+ 树是一种平衡的查找树，它可以有效组织存储大量的键值对，从而支持快速的插入和查找操作。 Go 语言可以用来实现 B+ 树，实现的思路是：首先，定义 B+ 树的结构，其…
阅读更多...
【Linux】安装Linux操作系统具体步骤

【Linux】安装Linux操作系统具体步骤

1). 选择创建新的虚拟机 2). 选择"典型"配置 3). 选择"稍后安装操作系统(S)" 4). 选择"Linux"操作系统,"CentOS7 64位"版本 5). 设置虚拟机的名称及系统文件存放路径 6). 设置磁盘容量 7). 自定义硬件信息 8). 启动上述创建的新虚拟机…
阅读更多...
【C++初阶】list的使用

【C++初阶】list的使用

大家好我是沐曦希&#x1f495; 文章目录一、前言二、构造三、迭代器四、增删查改1.头插头删2.尾插尾删3.查找和插入4.删除五、其他成员函数1.排序和去重2.splice和remove3.resize一、前言 list本质是带头双向循环链表&#xff0c;本文只对list的一些常用接口进行说明&#xf…
阅读更多...
Qt creator中操作QAction加入QToolBar

Qt creator中操作QAction加入QToolBar

背景&#xff1a;个人笔记。我之前没有系统化学习过任何资料&#xff0c;使用很多工具都是按需出发&#xff0c;直接上手&#xff0c;遇到问题再研究的。所以会有一些弯路。本文言语中难免有对个人情绪的生动描述&#xff0c;希望不要影响读者心情&#xff0c;这只是我学习过程…
阅读更多...
前端网络安全

前端网络安全

什么是同源策略同源指的是&#xff1a;协议、端口号、域名必须一致。他是浏览器的一个用于隔离潜在恶意文件的重要安全机制。限制了从同一个源加载的文档或脚本&#xff0c;与另一个源的资源进行交互。同源策略主要限制了三个方面&#xff1a;当前域下的js脚本不能够访问其他域…
阅读更多...
waf和web应用防火墙的区别

waf和web应用防火墙的区别

waf和web应用防火墙有什么区别?相信这两个词大家都不陌生&#xff0c;特别是做互联网行业的小伙伴们。对于waf和web应用防火墙&#xff0c;这两个名词的理解应该都很清楚。但是很多小伙伴们不知道WAF防火墙与Web防火墙有什么区别&#xff0c;它们之间的区别在哪里&#xff0c;…
阅读更多...
Spring Cloud(微服务)学习篇(七)

Spring Cloud(微服务)学习篇(七)

Spring Cloud(微服务)学习篇(七) 1.使用代码的方式实现流量限制规则 1.1 变更SentinelController类 1.1.1 加入的代码 //流控限制 (一个或多个资源限流), postConstruct注解的作用是保证项目一启动就会加载,// 一个rule就是一个规则PostConstructpublic void FlowRule(){Li…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023