L-norm Loss 系列

L1 Loss

别称
L1范数损失、最小绝对误差（LAD）、平均绝对值误差（MAE）
计算公式
$\operatorname{loss}(x, y)=\frac{1}{n} \sum_{i=1}^n\left|y_i-f\left(x_i\right)\right|$
其中 $y_i$ 是真实值， $f(x_i)$ 是预测值，n是样本点个数
导数
$\frac{\mathrm{d} L_1(x)}{\mathrm{d} x}= \begin{cases}1 & \text { if } x \geq 0 \\ -1 & \text { otherwise }\end{cases}$
特性
优点：无论对于什么样的输入值，都有着稳定的梯度，不会导致梯度爆炸问题，具有较为稳健性的解
缺点：在中心点是折点，不能求导，梯度下降时要是恰好学习到w=0就没法接着进行了
$L_1$ 损失函数对 x 的导数为常数，训练后期，x 很小时，如果学习率不变，损失函数会在稳定值附近波动，很难收敛到更高的精度。

L2 Loss

公式
$2=\sum_{i=1}^n\left(y_i-f\left(x_i\right)\right)^2$
导数
$\frac{\mathrm{d} L_2(x)}{\mathrm{d} x}=2 x$
特性
L2 loss由于是平方增长，因此学习快。L2损失函数对 x 的导数为2x，当 x 很大的时候，导数也很大，使L2损失在总loss 中占据主导位置，进而导致，训练初期不稳定。

Smooth L1 Loss

《Fast R-CNN》论文中首次提出Smooth L1 Loss

公式
$\operatorname{smooth}_{L_1}(x)= \begin{cases}0.5 x^2 & \text { if }|x|<1 \\ |x|-0.5 & \text { otherwise }\end{cases}$
其中 $x=y_i-f(x_i)$
导数
$\frac{\mathrm{d} \operatorname{smooth}_{L_1}}{\mathrm{~d} x}= \begin{cases}x & \text { if }|x|<1 \\ \pm 1 & \text { otherwis }\end{cases}$
特性
分析一下，当预测值f(xi)和真实值yi差别较小的时候（绝对值差小于1），其实使用的是L2 loss；差别大的时候，使用的是L1 loss的平移。因此，Smooth L1 loss其实是L1 loss 和L2 loss的结合，同时拥有两者的部分优点：
真实值和预测值差别较小时（绝对值差小于1），梯度也会比较小（损失函数比普通L1 loss在此处更圆滑）
真实值和预测值差别较大时，梯度值足够小（普通L2 loss在这种位置梯度值就很大，容易梯度爆炸）

IOU系列

IOU （2016）

论文地址：《UnitBox: An Advanced Object Detection Network》

提出背景
三种Loss用于计算目标检测的Bounding Box Loss时，独立的求出4个点的Loss，然后进行相加得到最终的Bounding Box Loss，这种做法的假设是4个点是相互独立的，实际是有一定相关性的
IoU (Intersection over Union)的计算
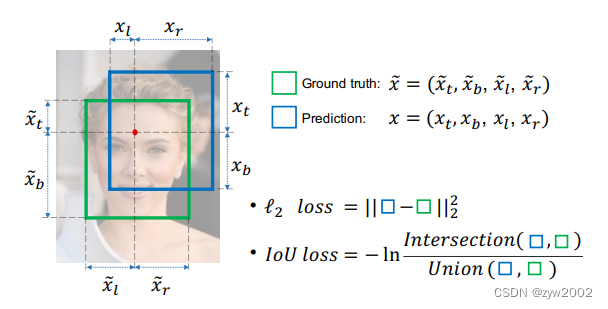
IOU的计算是用预测框(A)和真实框(B)的交集除以二者的并集，其公式为：
$U=\frac{A \cap B}{A \cup B}$
IoU的值越高也说明A框与B框重合程度越高，代表模型预测越准确。反之，IoU越低模型性能越差。
IOU Loss
$L_{IoU}=-ln(IoU)$
当IoU趋近为1时（两个框重叠程度很高），Loss趋近于0。IoU越小(两个框的重叠程度变低)，Loss越大。当IoU为0时（两个框不存在重叠），梯度消失。
IOU的特性
优点：
（1）IoU具有尺度不变性
（2）结果非负，且范围是(0, 1)
缺点：
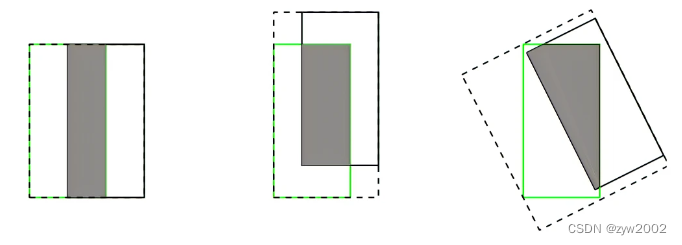
（1）如果两个目标没有重叠，IoU将会为０,并且不会反应两个目标之间的距离，在这种无重叠目标的情况下，如果IoU用作于损失函数，梯度为０，无法优化。
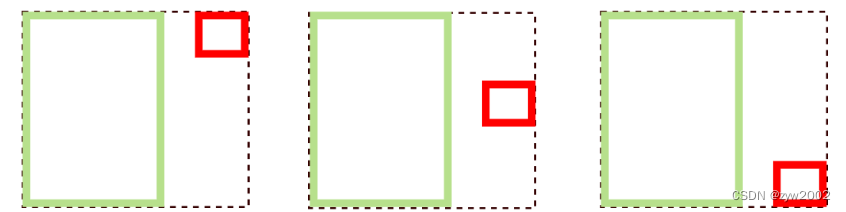
（2）IoU无法精确的反映两者的重合度大小。如下图所示，三种情况IoU都相等，但看得出来他们的重合度是不一样的，左边的图回归的效果最好，右边的最差。

GIOU （2019）

论文地址：《Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression》

提出背景
为了解决Iou的作为损失函数的缺点，提出了GIoU，在IoU后面增加了一项，计算两个框的最小外接矩形，用于表征两个框的距离，从而解决了两个目标没有交集时梯度为零的问题。
GIOU的计算
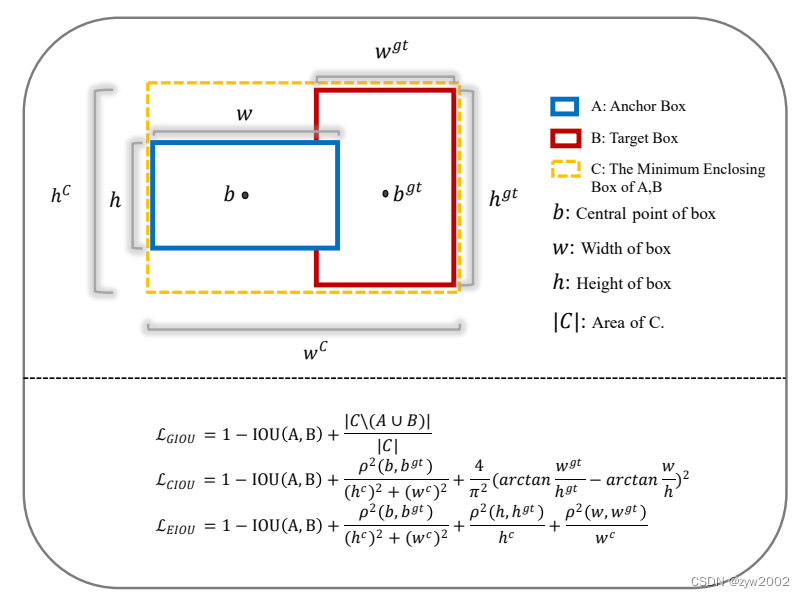
其中A表示真实框，B表示预测框，C表示两个框的最小外接矩形的面积。
$U-\frac{C-(A \cup B)}{C}$
当IoU=0时（A和B没有交集）：
$U=-1+\frac{A \cup B}{C}$
当A和B两个框离得越远，GIOU越接近-1；当两框重合时，GIOU=1。所以GIOU的取值为(-1,1]。
GIOU Loss
$L_{G I o U}=1-G I o U$
当 $A, B$ 两框不相交时， $\cup B$ 不变，最大化 $G I o U$ 就是最小化C, 这样会促进两个框不断靠近。
GIoU的特性
优点：
（1）当IoU=0时，仍然可以很好的表示两个框的距离。
（2）GIoU不仅关注重叠区域，还关注其他的非重合区域，能更好的反映两者的重合度
缺点：
（1）当两个框属于包含关系时，GIoU会退化成IoU，无法区分其相对位置关系，如下图：

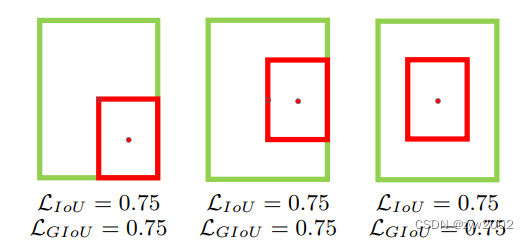
（2）由于GIoU仍然严重依赖IoU，因此在两个垂直方向，误差很大，很难收敛。两个框在相同距离的情况下，水平垂直方向时，此部分面积最小，对loss的贡献也就越小，从而导致在垂直水平方向上回归效果较差。
如下图，三种情况下GIoU的值一样，GIoU将很难区分这种情况。

DIOU （2020）

论文地址：《Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression》

提出背景

针对上述GIoU的两个问题，将GIoU中最小外接框来最大化重叠面积的惩罚项修改成最小化两个BBox中心点的标准化距离从而加速损失的收敛过程，这就诞生了DIoU。
DIoU要比GIou更加符合目标框回归的机制，将目标与预测之间的距离，重叠率以及尺度都考虑进去，使得目标框回归变得更加稳定，不会像IoU和GIoU一样出现训练过程中发散等问题。

DIOU的计算
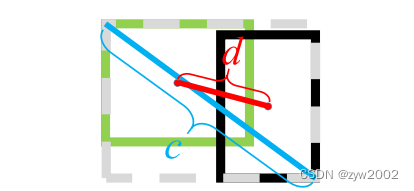
其中 $b, b^{g t}$ 分别代表了预测框和真实框的中心点，且 $\rho$ 代表的是计算两个中心点间的欧式距离。
c 代表的是能够同时包含预测框和真实框的最小外接矩形的对角线长度。
$U-\frac{\rho^2\left(b, b^{g t}\right)}{c^2}$
DIOU Loss
$L_{D I o U}=1-D I o U$
DIOU的特性
优点：
（1）DIoU loss可以直接最小化两个目标框的距离，因此比GIoU loss收敛快得多。
（2）对于包含两个框在水平方向和垂直方向上这种情况，DIoU损失可以使回归非常快。
（3）DIoU还可以替换普通的IoU评价策略，应用于NMS中，使得NMS得到的结果更加合理和有效。
缺点：
虽然DIOU能够直接最小化预测框和真实框的中心点距离加速收敛，但是Bounding box的回归还有一个重要的因素纵横比暂未考虑。如下图，三个红框的面积相同，但是长宽比不一样，红框与绿框中心点重合，这时三种情况的DIoU相同，证明DIoU不能很好的区分这种情况。

CIOU （2020）

论文地址：《Distance-IoU Loss: Faster and Better Learning for Bounding Box Regression》

提出背景
CIoU与DIoU出自同一篇论文，CIoU大多数用于训练。DIoU的作者考虑到，在两个框中心点重合时，c与d的值都不变。所以此时需要引入框的宽高比
CLoU的计算
$U-\left(\frac{\rho^2\left(b, b^{g t}\right)}{c^2}+\alpha v\right)$
其中 $\alpha$ 是权重函数， $\mathrm{v}$ 用来度量宽高比的一致性:
$\begin{gathered} \alpha=\frac{v}{(1-I o U)+v} \\ v=\frac{4}{\pi^2}\left(\arctan \frac{w_{g t}}{h_{g t}}-\arctan \left(\frac{w}{h}\right)\right)^2 \end{gathered}$
从 $v$ 可以看出， CIOU 中存在两个问题:
a. 使用的是预测框和目标框的宽高比，那当预测框的宽高满足 $\left\{\left(w^{\mathrm{p}}=k w^{\mathrm{gt}}, h^{\mathrm{p}}=k h^{\mathrm{gt}}\right) \mid k \in \mathbb{R}^{+}\right\}$ 时，CloU 中此项的惩罚便失去了作用。
b. 根据下面 $w^{\mathrm{p}}, h^{\mathrm{p}}$ 的梯度公式，
$\frac{\partial v}{\partial w^{\mathrm{p}}}=\frac{8}{\pi^2}\left(\arctan \frac{w^{\mathrm{gt}}}{h^{\mathrm{gt}}}-\arctan \frac{w^{\mathrm{p}}}{h^{\mathrm{p}}}\right) \cdot \frac{h^{\mathrm{p}}}{\left(w^{\mathrm{p}}\right)^2+\left(h^{\mathrm{p}}\right)^2}$
$\frac{\partial v}{\partial h^{\mathrm{p}}}=-\frac{8}{\pi^2}\left(\arctan \frac{w^{\mathrm{gt}}}{h^{\mathrm{gt}}}-\arctan \frac{w^{\mathrm{p}}}{h^{\mathrm{p}}}\right) \cdot \frac{w^{\mathrm{p}}}{\left(w^{\mathrm{p}}\right)^2+\left(h^{\mathrm{p}}\right)^2}$
可以得出， $\frac{\partial v}{\partial w^{\mathrm{p}}}=-\frac{h}{w} \frac{\partial v}{\partial h^{\mathrm{p}}}$ 两者的关系成反比。也就是说，训练时 $w^{\mathrm{p}}, h^{\mathrm{p}}$ 中任意一者增大时，另一者必然减小。
CIoU Loss
$L_{C I o U}=1-I o U+\frac{\rho^2\left(b, b^{g t}\right)}{c^2}+a v$
CIoU的特性
优点：考虑了框的纵横比，可以解决DIoU的问题。
缺点：通过CIoU公式中的v反映的纵横比的差异，而不是宽高分别与其置信度的真实差异，所以有时会阻碍模型有效的优化相似性。

EIOU （2022）

论文地址：《Focal and Efficient IOU Loss for Accurate Bounding Box Regression》

EIOU的提出背景
CIoU不能真实的反映宽高分别与其置信度的真实差异，
且损失函数忽略了正负样本不平衡的问题，即大量与目标框重叠面积较小的预测框在最终的 bbox 优化中占用了绝大部分的贡献。
为了解决CIoU的问题，有学者在CIOU的基础上将纵横比拆开，提出了EIOU Loss，并且加入Focal聚焦优质的预测框，与CIoU相似的，EIoU是损失函数的解决方案，只用于训练。
EIOU LOSS
EIOU的惩罚项是在CIOU的惩罚项基础上将纵横比的影响因子拆开分别计算目标框和预测框的长和宽，该损失函数包含三个部分：重叠损失，中心距离损失，宽高损失，前两部分延续CIoU中的方法，但是宽高损失直接使目标框与预测框的宽度和高度之差最小，使得收敛速度更快。惩罚项公式如下：
$\begin{gathered} L_{E I o U}=L_{I o U}+L_{d i c}+L_{a s p} \\ =1-I o u+\frac{\rho^2\left(b, b^{g t}\right)}{\left(c_w\right)^2+\left(c_h\right)^2}+\frac{\rho^2\left(w, w^{g t}\right)}{\left(c_w\right)^2}+\frac{\rho^2\left(h, h^{g t}\right)}{\left(c_h\right)^2} \end{gathered}$
其中 $b^{gt}$ 和 $b^p$ 分别表示预测框和目标框中心点的坐标。 $d(b^p,b^{gt})$ 表示二者的欧式距离。 $c_w$ 和 $c_h$ 是覆盖两个Box的最小外接框的宽度和高度。
FOCAL EIoU LOSS

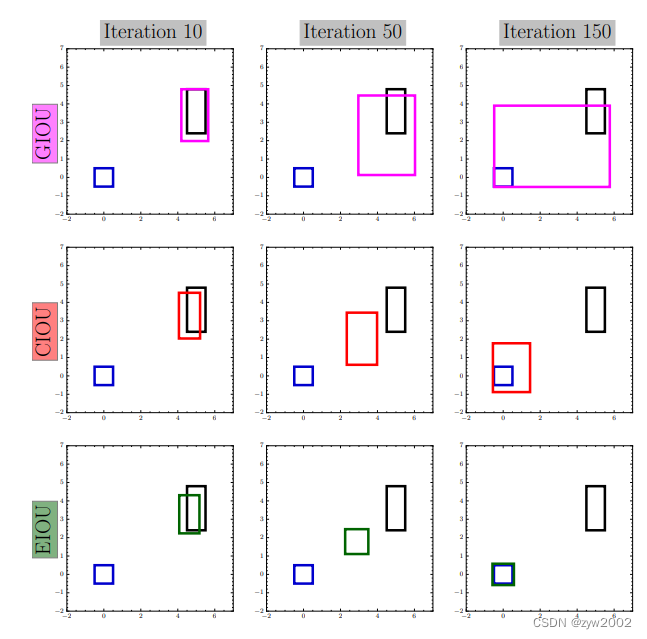
GIOU 通过预测框和目标框的差集/最小外界矩形来作为惩罚项，一方面在预测框在目标框内部或目标框在预测框内部时，都无法处理比值相同的情况；另一方面，也导致 GIOU 存在先减小差集面积再优化 IoU 值的可能性。
CIOU 存在的问题是上面提到的预测框宽高比成反比，两者不能同时增大或缩小。如上图第二行，iter=50 中预测框的宽高都大于目标框，但是在 iter=150 中，预测框的高变小，但是宽却变大。
上面提到第二个动机，目标检测模型中预测框往往数量较大，其中与目标框 IOU 值较低的低质量样本占绝大多数。低质量样本在训练时容易造成损失值波动的情况。作者认为高低质量样本分布不均是影响模型收敛的一个重要因素。作者提到，一个优秀的损失函数应该具有下面几个性质：
当回归的 error 是 0 的时候，此时的梯度也应当是 0，因为我们这时不再需要对参数进行调整；
在错误率小的地方，梯度的值也应当小，反之在错误率大的地方，梯度也应当大，因为这时候我们需要对错误率小的情况进行微调，而错误率大的地方进行大刀阔斧的调整；
应该有一个参数可以抑制低质量样本对损失值的影响；
梯度值的范围应该在一定的范围内，例如 (0,1]，避免造成梯度的剧烈波动。
借助 Focal Loss 的思想，作者提出了 Focal L1 Loss，具体过程大致为：作者通过设计出一个合适的梯度函数，并根据它的性质求出相关参数的关系，通过求积分得出最终的损失函数。具体推导见论文中。作者设计的 Focal L1 Loss 的梯度函数如下,
$\frac{\partial \mathcal{L}_f}{\partial x}= \begin{cases}-\alpha x \ln (\beta x) & , 0<x \leq 1 ; \frac{1}{e} \leq \beta \leq 1 \\ -\alpha \ln (\beta) & , x>1 ; \frac{1}{e} \leq \beta \leq 1\end{cases}$
最终得出的 Focal L1 Loss 损失函数公式为:
$\mathcal{L}_f(x)= \begin{cases}-\frac{\alpha x^2(2 \ln (\beta x)-1)}{4} & , 0<x \leq 1 ; \frac{1}{e} \leq \beta \leq 1 \\ -\alpha \ln (\beta) x+C & , x>1 ; \frac{1}{e} \leq \beta \leq 1\end{cases}$
$L_{\text {Focal-EIou }}=I o U^\gamma L_{E I o U}$
其中，为了保证函数连续，令 $\mathcal{L}_f(1)$ 求得 $C=\frac{2 \alpha \ln \beta+\alpha}{4}$ .

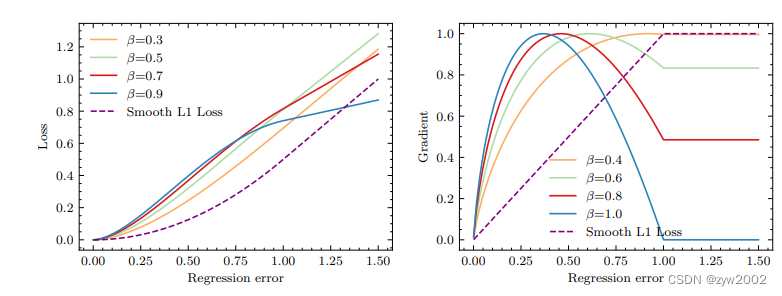
上图是 FocalL1 Loss 损失函数曲线 (a) 和其梯度曲线图 (b)。从 (b) 中可以看出，FocalL1 Loss 可以通过控制 $\beta$ 的大小来控制损失值超过 1 之后的梯度大小，如当 $\beta=1.0$ ，损失值大于 1 时，梯度值恒为 0 。而且，梯度曲线呈现出上凸趋势。当损失值过大或过小时，产生的梯度值均较小。当低质量样本产生损失值较大时，此时梯度值较小，以此来抑制低质量样本的贡献。
下图与上图类似，(a)是作者期望得到的损失函数梯度曲线；(b) 是 $\alpha=1, \beta$ 取不同值得到的损失函数图。

从以上两幅图中可以看出（论文中也有实验证明)，当 $\beta$ 越大时，低质量样本的梯度越小，即当损失值越大时，其产生梯度值越小，这里作者认为低质量样本会产生较大的梯度。与此相反，高质量样本的梯度越大。实验发现当 $\beta=0.8$ 时效果最好。
在具体使用中，FocalL1 Loss 通过计算预测框和目标框 $(x, y, w, h)$ 的位移偏差之和，来计算回归损失，如下式:
$\mathcal{L}_{\mathrm{loc}}=\sum_{i \in\{x, y, w, h\}} \mathcal{L}_f\left(\left|B_i^{\mathrm{p}}-B_i^{\mathrm{gt}}\right|\right)$
与 FocalL1 Loss 类似，作者还提出了 Focal-EloU Loss，如下:
$\mathcal{L}_{\text {Focal E-IoU }}=\mathrm{IoU}^\gamma \mathcal{L}_{\mathrm{EIoU}}$
Focal-EloU Loss 提出的原因是，作者在实验中发现当 $\mathcal{L}_{\mathrm{EIoU}}$ 接近零时，它的值非常小。同时， $\frac{\partial \mathcal{L}_f}{\partial \mathcal{L}_{\mathrm{EIoU}}}$ 也非常小。当两者相乘后，会得到更小的梯度值，这会使 $\mathcal{L}_{\mathrm{EIoU}}$ 较小的高质量样本的贡献大大降低。为了解决这个问题，作者通过 loU 值对 $\mathcal{L}_{\mathrm{EIoU}}$ 实现了权值的重置。以此来提高 $\mathcal{L}_{\mathrm{EIoU}}$ 较小的高质量样本的贡献。
同样是，通过实验发现较大的 $\gamma$ 值对于困难样本 (低质量样本)，即 IOU 较小的样本抑制效果较大，可能会延缓收敛速度、影响最终精度。当 $\gamma=0.5$ 获得最好的效果。

EIOU的特性
优点：
1）将纵横比的损失项拆分成预测的宽高分别与最小外接框宽高的差值，加速了收敛提高了回归精度。
2）引入了Focal Loss优化了边界框回归任务中的样本不平衡问题，即减少与目标框重叠较少的大量锚框对BBox 回归的优化贡献，使回归过程专注于高质量锚框。

αIOU (2021)

论文地址：《Alpha-IoU: A Family of Power Intersection over Union Losses for Bounding Box Regression》

αIOU 的提出背景
针对之前一系列IoU形式多且繁杂，αIOU 提出了一个对 IoU loss 的统一形式，通过 power transformation 来生成 IoU 和其对应惩罚项的统一形式，来动态调整不同 IoU 目标的 loss 和 gradient。
αIOU的计算
Box-Cox 变换：方差稳定变换，可以改变变量的分布，使得方差不再依赖于均值
当原始数据非正态分布，或者原始数据左偏、右偏时，需要对原始数据做一定的变换，经常会使用 Box-Cox 变换。
$\mathrm{y}(\lambda)=\left\{\begin{array}{l} \frac{y^\lambda-1}{\lambda}, \lambda \neq 0 \\ \ln y, \lambda=0 \end{array}\right.$

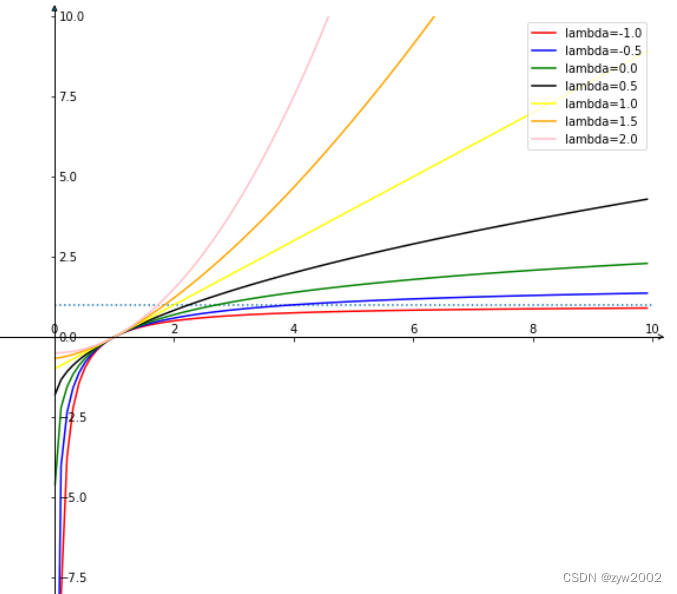
首先，在 loU loss $L_{I o U}=1-I o U$ 上使用 Box-Cox 变换，得到 $\alpha$ -loU:
$L_{\alpha-I o U}=\frac{\left(1-I o U^\alpha\right)}{\alpha}, \alpha>0$
对 $\alpha$ 的分析如下，可以得到很多形式:

当 $\alpha \rightarrow 0, \quad \lim _{\alpha \rightarrow 0} L_{\alpha-I o U}=-\log (I o U)=L_{\log (I o U)}$
当 $\alpha=1$ 时， $L_{1-I o U}=1-I o U=L_{I o U}$
当 $\alpha=2$ 时， $L_{2-I o U}=\frac{1}{2}\left(1-I o U^2\right)=\frac{1}{2} L_{I o U^2}$

对 $\alpha$ -loU 简化得到:
$\mathcal{L}_{\alpha-\mathrm{IoU}}=\left\{\begin{array}{l} -\log (I o U), \quad \alpha \rightarrow 0 \\ 1-I o U^\alpha, \quad \alpha \nrightarrow 0 . \end{array}\right.$
由于很多 loU-based 方法都是 $\alpha \nrightarrow 0$ 的，所以更多研究 $\alpha \nrightarrow 0$ 的情况，并且引入了一个惩罚项:
$\mathcal{L}_{\alpha-\mathrm{IoU}}=1-I o U^{\alpha_1}+\mathcal{P}^{\alpha_2}\left(B, B^{g t}\right)$

$\alpha_1>0, \alpha_2>0, P$ 是㤠罚项
作者后面证明了 $\alpha_2$ 对结果影响不大, 所以就让 $\alpha_1=\alpha_2$
有了上面的形式后，作者对不同的 loU-based 方法做了如下形式的统一，其实这些 loU-based loss 都可以看做是 $\alpha=1$ 时的特例:
$\ ( B ∪ B g t ) ∣ ∣ C ∣ ⟹ L α − G I o U = 1 − I o U α + ( ∣ C \ ( B ∪ B g t ) ∣ ∣ C ∣ ) α L D I o U = 1 − I o U + ρ 2 ( b , b g t ) c 2 ⟹ L α − D I o U = 1 − I o U α + ρ 2 α ( b , b g t ) c 2 α L C I o U = 1 − I o U + ρ 2 ( b , b g t ) c 2 + β v ⟹ L α − C l o U = 1 − I o U α + ρ 2 α ( b , b g t ) c 2 α + ( β v ) α , \begin{aligned} \mathcal{L}_{\mathrm{IoU}}=1-I o U & \Longrightarrow \mathcal{L}_{\alpha-\mathrm{IoU}}=1-I o U^\alpha \\ \mathcal{L}_{\mathrm{GIoU}}=1-I o U+\frac{\left|C \backslash\left(B \cup B^{g t}\right)\right|}{|C|} & \Longrightarrow \mathcal{L}_{\alpha-\mathrm{GIoU}}=1-I o U^\alpha+\left(\frac{\left|C \backslash\left(B \cup B^{g t}\right)\right|}{|C|}\right)^\alpha \\ \mathcal{L}_{\mathrm{DIoU}}=1-I o U+\frac{\rho^2\left(\boldsymbol{b}, \boldsymbol{b}^{g t}\right)}{c^2} & \Longrightarrow \mathcal{L}_{\alpha-\mathrm{DIoU}}=1-I o U^\alpha+\frac{\rho^{2 \alpha}\left(\boldsymbol{b}, \boldsymbol{b}^{g t}\right)}{c^{2 \alpha}} \\ \mathcal{L}_{\mathrm{CIoU}}=1-I o U+\frac{\rho^2\left(\boldsymbol{b}, \boldsymbol{b}^{g t}\right)}{c^2}+\beta v & \Longrightarrow \mathcal{L}_{\alpha-\mathrm{CloU}}=1-I o U^\alpha+\frac{\rho^{2 \alpha}\left(\boldsymbol{b}, \boldsymbol{b}^{g t}\right)}{c^{2 \alpha}}+(\beta v)^\alpha, \end{aligned}$

SIOU （2022）

论文地址：《SIoU Loss: More Powerful Learning for Bounding Box Regression Zhora Gevorgyan》

SIoU的提出背景
之前的IOU没有考虑到真实框与预测框框之间的方向，导致收敛速度较慢，对此SIoU引入真实框和预测框之间的向量角度，重新定义相关损失函数
SIoU的计算
(1) 角度损失(Angle cost)，定义如下:
$\Lambda=1-2 * \sin ^2\left(\arcsin \left(\frac{\mathrm{c}_{\mathrm{h}}}{\sigma}\right)-\frac{\pi}{4}\right)=\cos \left(2 *\left(\arcsin \left(\frac{\mathrm{c}_{\mathrm{h}}}{\sigma}\right)-\frac{\pi}{4}\right)\right)$
其中 $c_h$ 为真实框和预测框中心点的高度差， $\sigma$ 为真实框和预测框中心点的距离，事实上 $\arcsin \left(\frac{\mathrm{ch}}{\sigma}\right)$ 等于角度 $\alpha$
$\sigma=\sqrt{\left(b_{c_x}^{g t}-b_{c_x}\right)^2+\left(b_{c_y}^{g t}-b_{c y}\right)^2}$
$c_h=\max \left(b_{c_y}^{g t}, b_{c y}\right)-\min \left(b_{c_y}^{g t}, b_{c_y}\right)$
$\left(b_{c x}^{g t}, b_{c y}^{g t}\right)$ 为真实框中心坐标 $\left(b_{c_x}, b_{c_y}\right)$ 为预测框中心坐标，可以注意到当 $\alpha$ 为 $\frac{\pi}{2}$ 或 0 时，角度损失为 0 ，在训练过程中若 $\alpha<\frac{\pi}{4}$ ，则最小化 $\alpha$ ，否则最小化 $\beta$

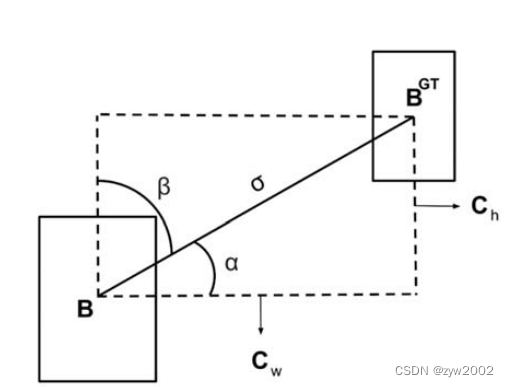
(2)距离损失(Distance cost)，定义如下：
$\Delta=\sum_{t=x, y}\left(1-\mathrm{e}^{-\gamma \rho_t}\right)=2-\mathrm{e}^{-\gamma \rho_{\mathrm{x}}}-\mathrm{e}^{-\gamma \rho_{\mathrm{y}}}$
其中:
$\rho_{\mathrm{x}}=\left(\frac{b_{c_{\mathrm{x}}}^{g t}-b_{c_{\mathrm{x}}}}{c_w}\right)^2, \quad \rho_{\mathrm{y}}=\left(\frac{b_{\mathrm{b}_{\mathrm{y}}}^{\mathrm{gt}}-b_{c_{\mathrm{y}}}}{c_{\mathrm{h}}}\right)^2 \quad \gamma=2-\Lambda$
注意: 这里的 $\left(c_{\mathrm{w}}, \mathrm{c}_{\mathrm{h}}\right)$ 为真实框和预测框最小外接矩形的宽和高

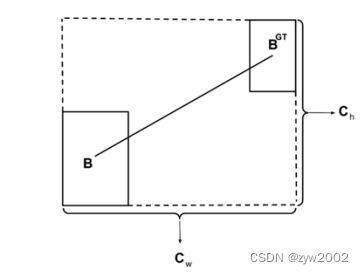
（3）形状损失(Shape cost)，定义如下：
$\Omega=\sum_{\mathrm{t}=\mathrm{w}, \mathrm{h}}\left(1-\mathrm{e}^{-\mathrm{wt}}\right)^\theta=\left(1-\mathrm{e}^{-\mathrm{ww}}\right)^\theta+\left(1-\mathrm{e}^{-\mathrm{wh}}\right)^\theta$
其中:
$w_w=\frac{\left|\mathrm{w}-\mathrm{w}^{\mathrm{gt}}\right|}{\max \left(\mathrm{w}, \mathrm{w}^{\mathrm{gt}}\right)}, \quad \mathrm{w}_{\mathrm{h}}=\frac{\left|\mathrm{h}-\mathrm{h}^{\mathrm{gt}}\right|}{\max \left(\mathrm{h}, \mathrm{h}^{\mathrm{gt}}\right)}$
$(w, h)$ 和 $\left(w^{\mathrm{gt}}, h^{\mathrm{gt}}\right)$ 分别为预测框和真实框的宽和高， $\theta$ 控制对形状损失的关注程度，为了避免过于关注形状损失而降低对预测框的移动，作者使用遗传算法计算出 $\theta$ 接近 4 ，因此作者定于 $\theta$ 参数范围为 $[2$ , 6]
SIoU Loss
$\operatorname{Loss}_{\mathrm{SIoU}}=1-\mathrm{IoU}+\frac{\Delta+\Omega}{2}$