18、多维图形绘制

一、三维图形绘制

（一）曲线图绘制plot3()

（二）网格图绘制 mesh()

（三）曲面图绘制 surf()

（四）光照模型 surfl()

（五）等值线图(等高线图)绘制 contour()

四、四维图形可视化

（一）用颜色描述第四维

（二）其他函数

一、三维图形绘制

（一）曲线图绘制plot3()

在三维图形指令中，plot3指令与plot指令类似，其调用格式如下：

plot3(X,Y,Z):X、Y、Z为同维向量时，绘制以X、Y、Z为x、y、z坐标的三维曲线；X、Y、Z为同维矩阵时，用X、Y、Z的对应列元素绘制x、y、z坐标的三维曲线，曲线的条数为矩阵的列数。
plot3(X1,Y1,Z1,X2,Y2,Z2)：绘制以X1、Y1、Z1和X2、Y2、Z2为x、y、z坐标的三维曲线。
plot3(X,Y,Z,'PropertyName',PropertyValue,...)：在PropertyName所规定的曲线属性下，绘制以X、Y、Z为x、y、z坐标的三维曲线。
plot3(X1,Y1,Z1,'PropertyName1',PropertyValue1,X2,Y2,Z2,'PropertyName2',ProperValue2)：在 PropertyName1所规定的曲线属性下，绘制以 X1、Y1、Z1为 x、y、z坐标的三维曲线；在PropertyName2所规定的曲线属性下，绘制以X2、Y2、Z2为x、y、z坐标的三维曲线。需要说明的是，plot3指令用来表现的是单参数的三维曲线，而非双参数的三维曲面。

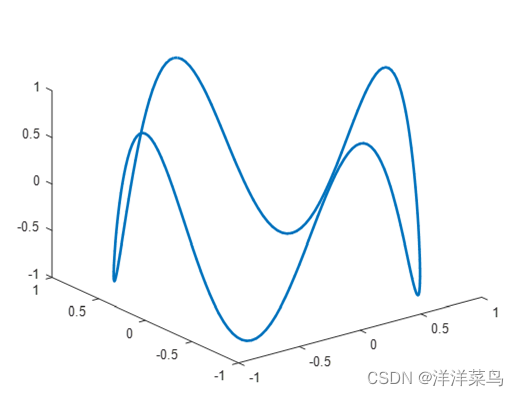
例1：plot3指令使用示例

clear;
clc;
theta=0:0.01*pi:pi*2;
x=sin(theta);
y=cos(theta);
z=cos(4*theta);
figure
plot3(x,y,z,'LineWidth',2);hold on;

运行结果：

（二）网格图绘制 mesh()

三维网格图和曲面图的绘制比三维曲线图更复杂，主要是因为绘图数据的准备及三维图形的色彩、明暗、光照和视角等的处理。

绘制函数z=f(x,y)的三维网格图的过程如下：

（1）确定自变量x和y的取值范围和取值间隔

（2）构成xoy平面上的自变量采样“格点”矩阵。

①利用“格点”矩阵的原理生成矩阵。

②利用meshgrid指令生成“格点”矩阵。

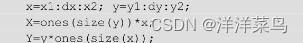
（3）计算在自变量采样“格点”上的函数值：Z=f(X,Y)。

绘制网格图的基本mesh指令的调用格式如下：

mesh(X,Y,Z)：以X为x轴自变量、Y为y轴自变量，绘制网格图；X、Y均为向量，若X、Y长度分别为m、n，则Z为m×n的矩阵，即[m,n]=size(Z)，则网格线的顶点为(Xj,Yi,Zij)。
mesh(Z)：以Z矩阵列下标为x轴自变量、行下标为y轴自变量，绘制网格图。
mesh(X,Y,Z,C)：以X为x轴自变量、Y为y轴自变量，绘制网格图；其中C用于定义颜色，如果不定义 C，则成为 mesh(X,Y,Z)，其绘制的网格图的颜色随着 Z 值的变化（即曲面高度）而变化。
mesh(X,Y,Z,'PropertyName ',PropertyValue,...)：以X为x轴自变量、Y为y轴自变量，绘制网格图；PropertyValue用来定义网格图的标记等属性。

例2：mesh指令使用示例

clear;
clc;
x=-10:0.1:10;y=-10:0.1:10;
[x,y]=meshgrid(x,y);
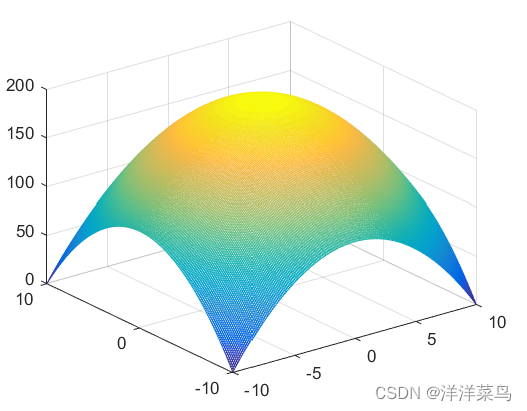
z=-x.^2-y.^2+200;
mesh(x,y,z)

运行结果：

（三）曲面图绘制 surf()

曲面图的绘制由surf指令完成，该指令的调用格式与mesh指令类似，具体如下：

surf (X,Y,Z)。
surf (Z)。
surf (X,Y,Z,C)。
surf(X,Y,Z,'PropertyName',PropertyValue,...)。

mesh指令所绘制的图形是网格划分的曲面图，而surf指令绘制得到的是平滑着色的三维曲面图，着色的方式是在得到相应的网格点后，对每一个网格依据该网格所代表的节点的色值（由变量C控制）来定义这一网格的颜色。

例3：surf指令与mesh指令对比

clear;
clc;
[x,y,z]=peaks(25);
figure
subplot(1,2,1);surf(x,y,z)
subplot(1,2,2);mesh(x,y,z)

运行结果：

（四）光照模型 surfl()

光照是一种利用方向光源来照亮物体的技术。在某些情况下，这项技术能使表面微妙的差异更容易看到，光照也可以增强三维图像的现实感

例4：带光照的曲面图

clear;
clc;
x=-10:0.1:10;y=-10:0.1:10;
[x,y]=meshgrid(x,y);
z=-x.^2-y.^2+200;
figure
surf(x,y,z,'FaceColor','r','EdgeColor','none');
camlight left;lighting phong
view(-15,65)

运行结果：

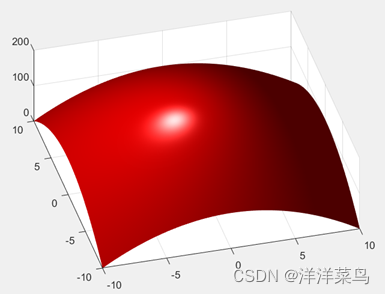
本例中将曲面涂上了红色，并且将surf指令所定义的网格线移除。同时，一个发光的物体被加到了“镜头”的左边（即从空间观看时所在表面的位置）。增加光源和设置好照明方式到phong后，使用view命令去改变视角，从空间的另一个不同的点再观看表面（方位角-15°和仰角65°）。最后，用工具栏缩放方式放大外观。

基于运用漫射、镜面反光和环境照明模型，MATLAB中还内置了surfl函数，可以画出类似于函数surf产生的带彩色的曲面。使用一个单色颜色映像（如灰色、纯白、铜黄或粉红色）和插值色彩，会画出效果更好的曲面。其调用格式如下：

surfl(X,Y,Z,S)：其中S以[Sx,Sy,Sz]或[az,el]的形式定义光源方向。

在没有明确定义的情况下，其默认光源是逆时针45°。

例5：surfl指令应用示例

clear;
clc;
[x,y,z]=peaks(25);
figure
subplot(1,2,1);surfl(x,y,z),colormap(copper),shading interp
subplot(1,2,2);surfl(x,y,z,[-90 30],[0.55  0.6 2 10]),shading interp

运行结果：

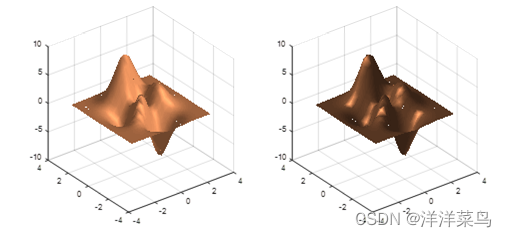
（五）等值线图(等高线图)绘制 contour()

绘制等值线图需要用到contour指令，其调用格式如下：

contour(Z) 以Z矩阵的列下标为x轴自变量、行下标为y轴自变量，绘制等值线图
contour(Z,n) n为所绘制的图形等值线的条数
contour(Z,v) v为向量，向量长度为等值线的条数，并且等值线的值为对应的向量的元素值
contour(X,Y,Z) 以X为x轴自变量、Y为y轴自变量，绘制等值线XY均为向量，若X、Y长度分别为m、n，则Z为m*n的矩阵，即[m,n]]=size(Z)，网格线的顶点为(X(j),Y(i),Z(i,j))
contour(X,Y,Z,n)：其中n为所绘制的图形等值线的条数。
contour(X,Y,Z,v)：其中v为向量，向量的长度为等值线的条数，并且等值线的值为对应的向量的元素值。
surf(...,LineSpec)：其中LineSpec用来定义等值线的线型。

与contour作用相类似的指令还有contourf指令，其调用格式与contour相同。

例6：contour指令使用示例

clear;
clc;
[x,y,z]=peaks(25);
figure
subplot(2,2,1);contour(x,y,z);axis square
subplot(2,2,2);contour(x,y,z,10);axis square
subplot(2,2,3);contour(x,y,z,-10:1:10);axis square
subplot(2,2,4);contour(x,y,z,':');axis square

运行结果：

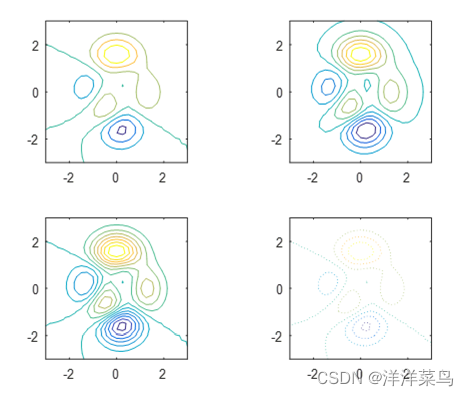
四、四维图形可视化

（一）用颜色描述第四维

用mesh和surf等指令所绘制的图像，在未给出颜色参量的情况下，图像的颜色是沿着z轴的数据变化的。将颜色施加于z轴能够产生色彩亮丽的图画，但由于z轴已经存在，因此它并不提供新的信息。但使用颜色来描述不受3个轴影响的数据的某些属性，需要赋给三维作图函数的颜色参量所需要的“第四维”的数据。

如果作图函数的颜色参量是一个向量或矩阵，那么就用作颜色映像的下标。这个参量可以是任何实向量或与其参量维数相同的矩阵。

例7：使用颜色描述第四维示例

clear;
clc;
[x,y,z]=peaks(25);
r=sqrt(x.^2+y.^2)
figure
subplot(1,2,1);surf(x,y,z,z);axis tight
subplot(1,2,2);surf(x,y,z,r);axis tight

运行结果：

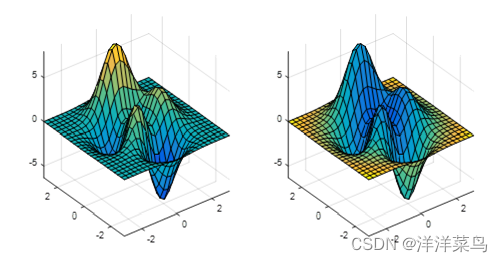
其中，在坐标系中描述一个面需要三维数据，而另一维数据描述空间中的点的坐标值，则使用不同的颜色表现出来；在左图中，第四维数据为Z；在右图中，第四维数据为R；在图上可以看到两者的颜色分布发生了明显的变化。

（二）其他函数

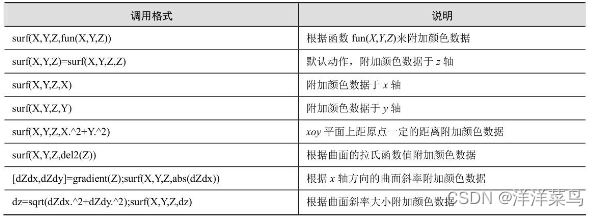
除了上述的函数，slice函数也可以通过颜色来表示存在于第四维空间中的值，其调用格式如下：

slice(V,nx,ny,nz)：显示三元函数V(X,Y,Z)确定的立体图在x轴、y轴、z轴方向上的若干点（对应若干平面）的切片图，各点的坐标由数量向量sx、sy、sz指定。其中V为大小为m×n×p的三维数组，默认值为X=1:m、Y=1:n、Z=1:p。
slice(X,Y,Z,V,nx,ny,nz)：显示三元函数V(X,Y,Z)确定的立体图在x轴、y轴、z轴方向上的若干点（对应若干平面）的切片图。若函数V(X,Y,Z)中有一个变量X取定值X0，则函数V(X0,Y,Z)为X=X0立体面的切面图（将该切面通过颜色表示V的值），各点的坐标由数量向量sx、sy、sz指定。参量X、Y、Z均为三维数组，用于指定立方体V的每点的三维坐标。
slice(V,XI,YI,ZI)：显示由参量矩阵 XI、YI、ZI 确定的立体图的切片图，参量XI、YI、ZI定义了一个曲面，同时会在曲面的点上计算立体图V的值。需要注意的是，XI、YI、ZI必须为同型矩阵。
slice(X,Y,Z,V,XI,YI,ZI)：沿着由矩阵XI、YI、ZI定义的曲面穿过立体图V的切片图。
slice(...,'method')：通过method来指定内插值的方法，method可取linear、cubic、nearest。linear指定的内插值方法为三次线性内插值（若未指定，此即为默认值）,cubic指定使用三次立方内插值法，nearest指定使用最近点内插值法。

例8：slice函数示例

clear;
clc;
[x,y,z] = meshgrid(0:.5:10,0:.5:10,0:.5:10);
c = x.^2+y.^2+z.^2;
xs = [0,2,4,6,8,10];
ys = [4];
zs = [6]; % xs,ys,zs可决定切片形式和位置，helpslice可明白其具体含义
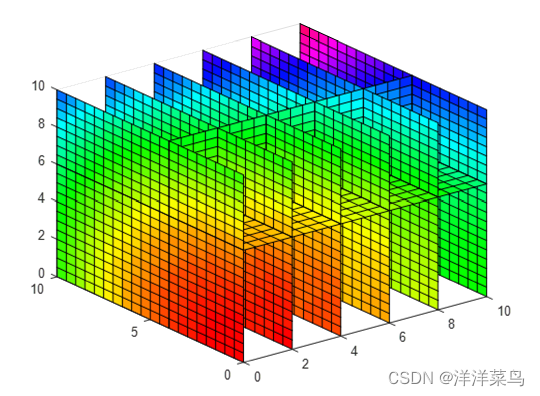
slice(x,y,z,c,xs,ys,zs)
colormap hsv

运行结果：