python实现PCA降维画分类散点图并标出95%的置信区间

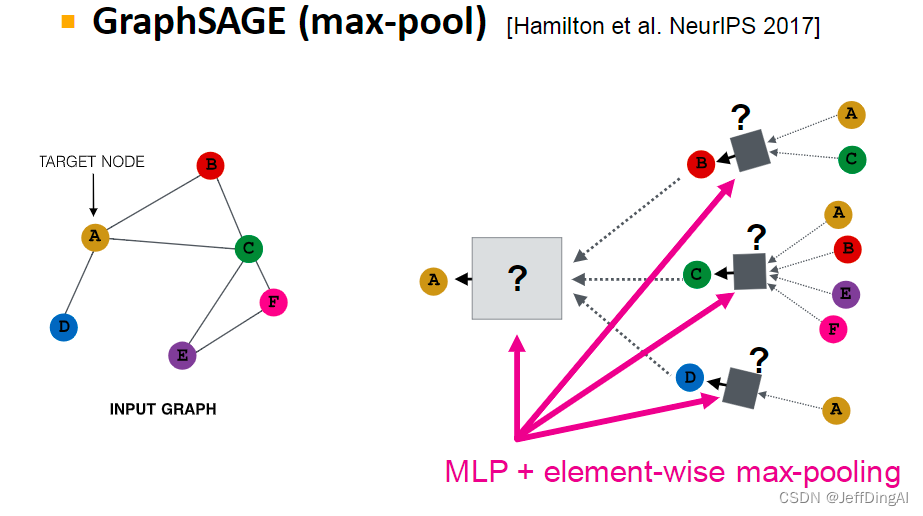
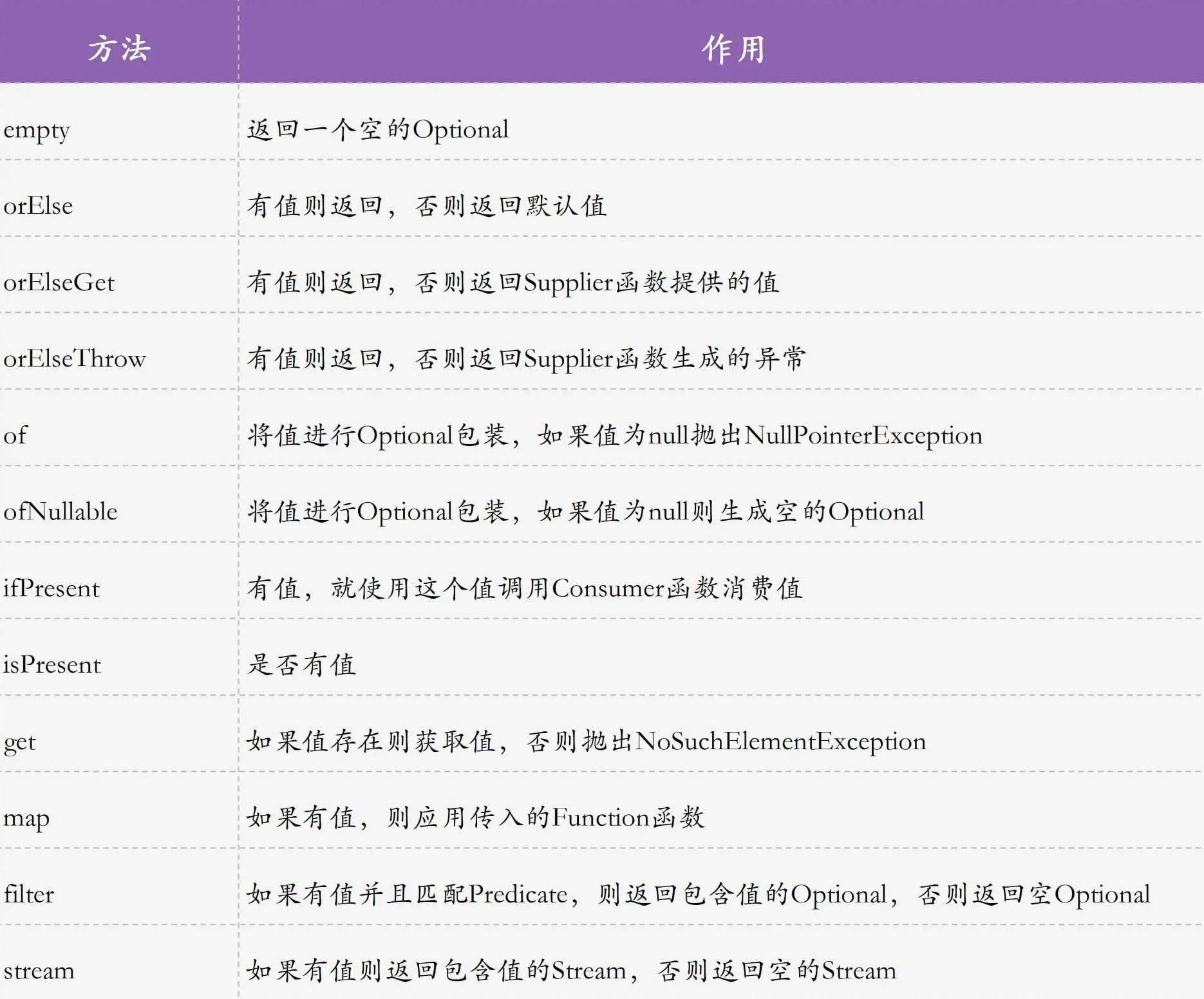
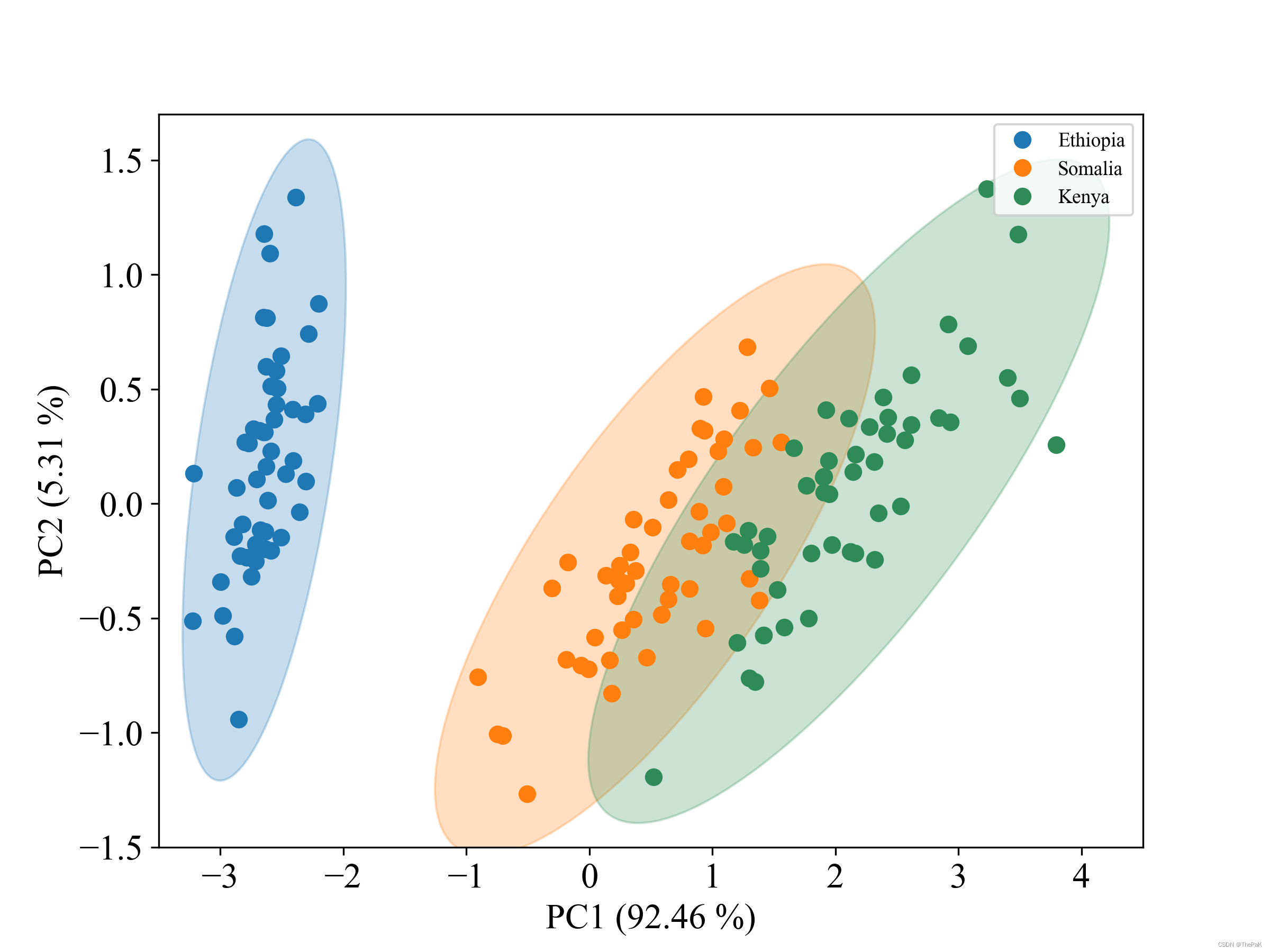
此代码以数据集鸢尾花为例，对其使用PCA降维后，绘制了三个类别的样本点和对应的置信圆（即椭圆）。先放效果图。

下面是完整代码：

from matplotlib.patches import Ellipse

def plot_point_cov(points, nstd=3, ax=None, **kwargs):
    # 求所有点的均值作为置信圆的圆心
    pos = points.mean(axis=0)
    # 求协方差
    cov = np.cov(points, rowvar=False)

    return plot_cov_ellipse(cov, pos, nstd, ax, **kwargs)

def plot_cov_ellipse(cov, pos, nstd=3, ax=None, **kwargs):
    def eigsorted(cov):
        cov = np.array(cov)
        vals, vecs = np.linalg.eigh(cov)
        order = vals.argsort()[::-1]
        return vals[order], vecs[:, order]
    if ax is None:
        ax = plt.gca()
    vals, vecs = eigsorted(cov)

    theta = np.degrees(np.arctan2(*vecs[:, 0][::-1]))
    width, height = 2 * nstd * np.sqrt(vals)
    ellip = Ellipse(xy=pos, width=width, height=height, angle=theta, **kwargs)
    ax.add_artist(ellip)
    return ellip

'''画置信圆'''
def show_ellipse(X_pca, y, pca, flag=1):
    # 定义颜色

    colors = ['tab:blue', 'tab:orange', 'seagreen']
    regions = ['Ethiopia', 'Somalia', 'Kenya']

    # 定义分辨率
    plt.figure(dpi=300, figsize=(8, 6))
    # 三分类则为3
    for i in range(0, 3):
        pts = X_pca[y == int(i), :]
        new_x, new_y = X_pca[y==i, 0], X_pca[y==i, 1]

        plt.plot(new_x, new_y, '.', color=colors[i], label=regions[i], markersize=14)

        plot_point_cov(pts, nstd=3, alpha=0.25, color=colors[i])

    # 添加坐标轴
    plt.xlim(-3.5, 4.5)
    plt.ylim(-1.5, 1.7)
    plt.xticks(size=16, family='Times New Roman')
    plt.yticks(size=16, family='Times New Roman')
    font = {'family': 'Times New Roman', 'size': 16}
    plt.xlabel('PC1 ({} %)'.format(round(pca.explained_variance_ratio_[0] * 100, 2)), font)
    plt.ylabel('PC2 ({} %)'.format(round(pca.explained_variance_ratio_[1] * 100, 2)), font)

    plt.legend(prop={"family": "Times New Roman", "size": 9},  loc='upper right')
    plt.show()

import pandas as pd
from sklearn.decomposition import PCA
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
labels = ['setosa', 'versicolor', 'virginica']
iris = load_iris()
X = iris.data
y = iris.target_names[iris.target]

print("y length--------", len(y))
y_category = pd.Categorical(y,ordered=True,categories=['setosa', 'versicolor', 'virginica'])

y = y_category.codes
print(y)
print(y.shape)
print(type(y[0]))
n_components = 2
pca = PCA(n_components=n_components)
X_pca = pca.fit_transform(X)
show_ellipse(X_pca, y, pca)

下面讲解实现过程。

首先导入需要的库和数据集：

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from matplotlib.patches import Ellipse

然后定义了一个函数 plot_point_cov()，用于计算样本点的协方差矩阵，并调用另一个函数 plot_cov_ellipse()，绘制置信椭圆。

代码中的cov变量是用于计算数据集协方差矩阵的。协方差矩阵用于描述多个变量之间的关系，其中对角线上的元素表示每个变量本身的方差，非对角线上的元素表示不同变量之间的协方差。

在函数plot_cov_ellipse()中使用协方差矩阵计算数据集的特征向量和特征值。特征向量和特征值用于确定椭圆的大小和方向，以便绘制置信椭圆。

因为在二维空间中，椭圆的方向和大小可以用特征向量和特征值来描述。例如对于一个2x2的协方差矩阵cov，它有两个特征向量和两个特征值，分别表示数据集在两个主要方向上的方差和偏移。特征向量的方向决定了椭圆的主轴方向，而特征值的大小则决定了椭圆沿每个主轴的长度。

在函数plot_cov_ellipse()中，先使用np.linalg.eigh()函数计算协方差矩阵cov的特征值和特征向量，然后按特征值从大到小的顺序排序，这样可以确保主轴方向是正确的。然后根据主轴方向的角度和特征值计算椭圆的宽度和高度，进而绘制置信椭圆。函数np.degrees()用于将弧度转换为角度，函数np.arctan2()用于计算角度。

np.degrees() 该函数使用的公式：角度=弧度*180/pi

np.degrees() 函数的参数是 np.arctan2(*vecs[:, 0][::-1])，它表示计算向量 vecs 中第一列（即下标为 0 的列）的极角（即与 x 轴的夹角）并将结果转换为角度制。

具体来说，vecs[:, 0] 表示选取 vecs 中所有行的第一列组成的向量，[::-1] 表示将该向量反转，从而得到与 arctan2 函数所需的参数格式一致的向量。

然后，np.arctan2() 函数接收两个参数，表示计算以这两个参数组成的向量为起点，与原点连接的向量的极角。这里第一个参数是反转后的向量，即 vecs[:, 0][::-1]，第二个参数未给出，因此默认为 1。

最后，np.degrees() 函数将弧度制的极角值转换为角度制。因此，整个代码行的作用是计算向量 vecs 的第一列的极角，并将结果转换为角度制。

vals, vecs = eigsorted(cov)其目的是计算输入协方差矩阵的特征值和特征向量并返回排好序的结果。

特征值（eigenvalues）是协方差矩阵的一个重要属性，代表着每个特征向量的方差。在PCA中，特征值告诉我们每个主成分解释方差的大小。排序特征值后，我们可以选择最大的K个特征值来保留大部分数据的方差。

特征向量（eigenvectors）是PCA中另一个重要的概念，它们是协方差矩阵的正交基向量。每个特征向量对应着一个特征值。它们可以用来表示主成分的方向，PCA中的主成分就是按特征值大小排序后的特征向量。PCA的主要目的就是通过旋转坐标系来最大化每个主成分方差。

特征向量在这里被用来求出主成分的方向。在函数中，特征向量通过 vecs[:, order] 得到， [:, order] 表示选中所有行（ : ）和按照特定顺序排序的所有列（ order ）。这些特征向量就是主成分方向的坐标轴，可以用来画出置信区间椭圆的角度。

椭圆的角度可以通过主成分方向的坐标轴与水平轴的夹角得到。在给定的代码中， theta 被计算为 np.degrees(np.arctan2(*vecs[:, 0][::-1]))，其中 arctan2() 计算向量的反正切值， [::-1] 表示按照相反的顺序取向量的元素。 np.degrees() 将弧度转换为角度。

def plot_point_cov(points, nstd=3, ax=None, **kwargs):
    # 求所有点的均值作为置信圆的圆心
    pos = points.mean(axis=0)
    # 求协方差矩阵
    cov = np.cov(points, rowvar=False)

    return plot_cov_ellipse(cov, pos, nstd, ax, **kwargs)

def plot_cov_ellipse(cov, pos, nstd=3, ax=None, **kwargs):
    def eigsorted(cov):
        cov = np.array(cov)
        vals, vecs = np.linalg.eigh(cov)
        order = vals.argsort()[::-1]
        return vals[order], vecs[:, order]

    if ax is None:
        ax = plt.gca()
    vals, vecs = eigsorted(cov)

    theta = np.degrees(np.arctan2(*vecs[:, 0][::-1]))
    width, height = 2 * nstd * np.sqrt(vals)
    ellip = Ellipse(xy=pos, width=width, height=height, angle=theta, **kwargs)
    ax.add_artist(ellip)
    return ellip

最后，定义了一个函数 show_ellipse()，用于绘制样本点和置信椭圆。

'''画置信圆'''
def show_ellipse(X_pca, y, pca, flag=1):
    # 定义颜色
    colors = ['tab:blue', 'tab:orange', 'seagreen']
    regions = ['Ethiopia', 'Somalia', 'Kenya']

    # 定义分辨率
    plt.figure(dpi=300, figsize=(8, 6))
    # 三分类则为3
    for i in range(0, 3):
        pts = X_pca[y == int(i), :]
        new_x, new_y = X_pca[y==i, 0], X_pca[y==i, 1]

        plt.plot(new_x, new_y, '.', color=colors[i], label=regions[i], markersize=14)

        plot_point_cov(pts, nstd=3, alpha=0.25, color=colors[i])

    # 添加坐标轴
    plt.xlim(-3.5, 4.5)
    plt.ylim(-1.5, 1.7)
    plt.xticks(size=16, family='Times New Roman')
    plt.yticks(size=16, family='Times New Roman')
    font = {'family': 'Times New Roman', 'size': 16}
    plt.xlabel('PC1 ({} %)'.format(round(pca.explained_variance_ratio_[0] * 100, 2)), font)
    plt.ylabel('PC2 ({} %)'.format(round(pca.explained_variance_ratio_[1] * 100, 2)), font)

    plt.legend(prop={"family": "Times New Roman", "size": 9},  loc='upper right')
    plt.show()

以数据集鸢尾花为例进行PCA降维，并使用上面代码画置信圆。

import pandas as pd
from sklearn.decomposition import PCA
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
labels = ['setosa', 'versicolor', 'virginica']
iris = load_iris()
X = iris.data
y = iris.target_names[iris.target]

print("y length--------", len(y))
y_category = pd.Categorical(y,ordered=True,categories=['setosa', 'versicolor', 'virginica'])

y = y_category.codes
print(y)
print(y.shape)
print(type(y[0]))
n_components = 2
pca = PCA(n_components=n_components)
X_pca = pca.fit_transform(X)
show_ellipse(X_pca, y, pca)

上面解析均为学习使用，如有问题请指正。