题目： 编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」 定义为：对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
如果这个过程 结果为 1，那么这个数就是快乐数。如果 n 是快乐数就返回 true ；不是则返回 false 。

示例 1：

输入：n = 19
输出：true
解释：
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1

示例 2：

输入：n = 2
输出：false

思路：

根据推理，猜测会有以下三种可能。

1. 最终会得到1。
2. 最终会进入循环。
3. 值会越来越大，最后接近无穷大。

第三个情况比较难以检测和处理。怎么知道它会继续变大，而不是最终得到1呢？仔细想一想，每一位数的最大数字的下一位数是多少。

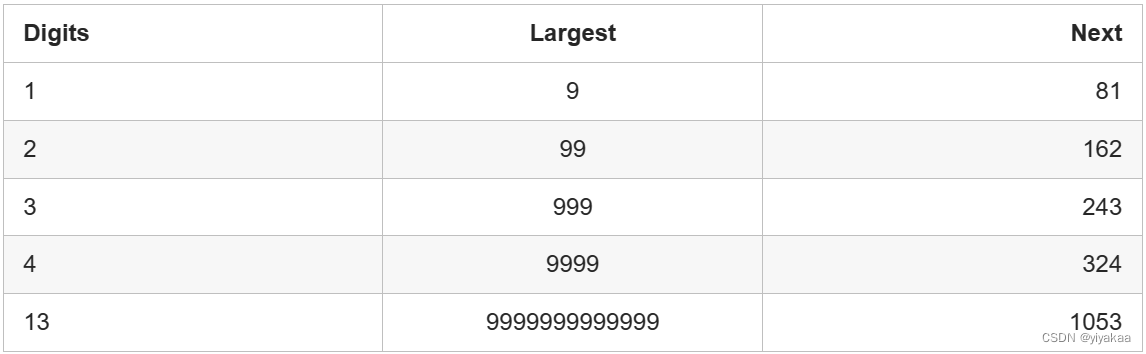
对于 3 位数的数字，它不可能大于 243。这意味着它要么被困在 243 以下的循环内，要么跌到 1。4 位或 4 位以上的数字在每一步都会丢失一位，直到降到 3 位为止。所以我们知道，最坏的情况下，算法可能会在 243 以下的所有数字上循环，然后回到它已经到过的一个循环或者回到 1。但它不会无限期地进行下去，所以我们排除第三种选择。

即使在代码中不需要处理第三种情况，仍然需要理解为什么它永远不会发生，这样就可以证明为什么不处理它。

算法

算法分为两部分，我们需要设计和编写代码。

1. 给一个数字 n，它的下一个数字是什么？
2. 按照一系列的数字来判断我们是否进入了一个循环。

第 1 部分我们按照题目的要求做数位分离，求平方和。
第 2 部分可以使用哈希集合完成。每次生成链中的下一个数字时，我们都会检查它是否已经在哈希集合中。

• 如果它不在哈希集合中，我们应该添加它。
• 如果它在哈希集合中，这意味着我们处于一个循环中，因此应该返回 false 。

class Solution {
public:
	int getresult(int n) {
		int num = 0;
		while (n) {
			num = num + (n % 10) * (n % 10);
			n = n / 10;
		}
		return num;
	}
	bool ishappy(int n) {
		unordered_set<int> result;
		while (1) {
			int num = getresult(n);
			if (num == 1) {
				return true;
			}
			if (result.find(num) != result.end()) {
				return false;
			}
			else {
				result.insert(num);
			}
			n = num;
		}
	}

};
int main() {
	Solution s;
	cout<< s.ishappy(12) << endl;
	return 0;
}