文章目录

运算方法和运算电路
- 基本运算部件
- 定点数的移位运算
- - 算术移位
  - 逻辑移位
  - 循环移位
- 定点数的加减运算
- - 原码的加减法
  - 补码的加减法
  - 原码的乘法
  - 补码的乘法
  - 原码的除法
  - 补码的除法
- 符号扩展
- 大小端和内存对齐
- 刷题小结
- 最后

运算方法和运算电路

基本运算部件

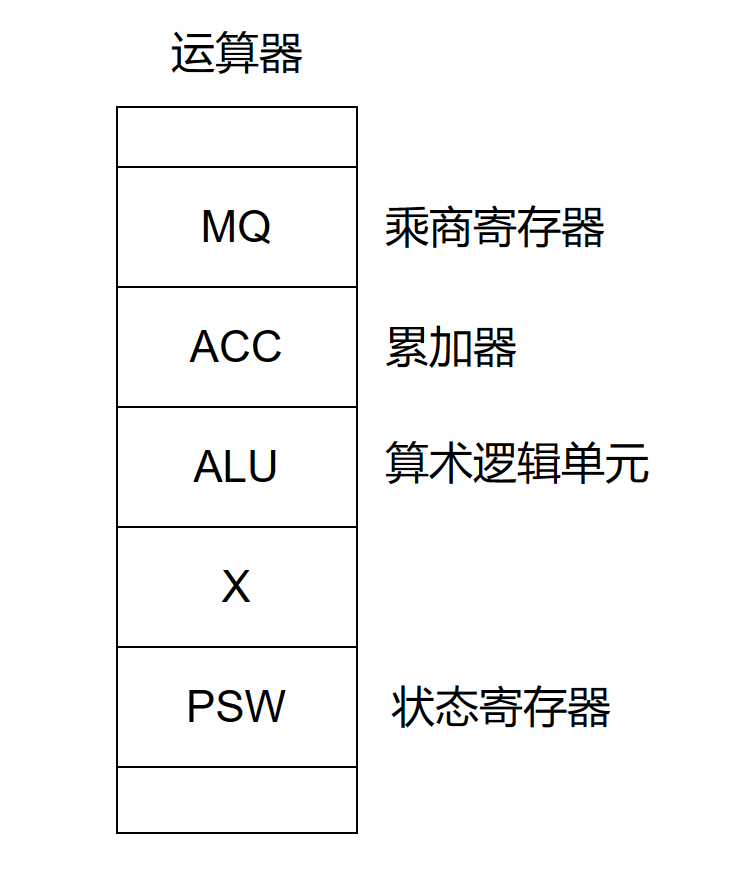
运算器一般包含这么几部分：

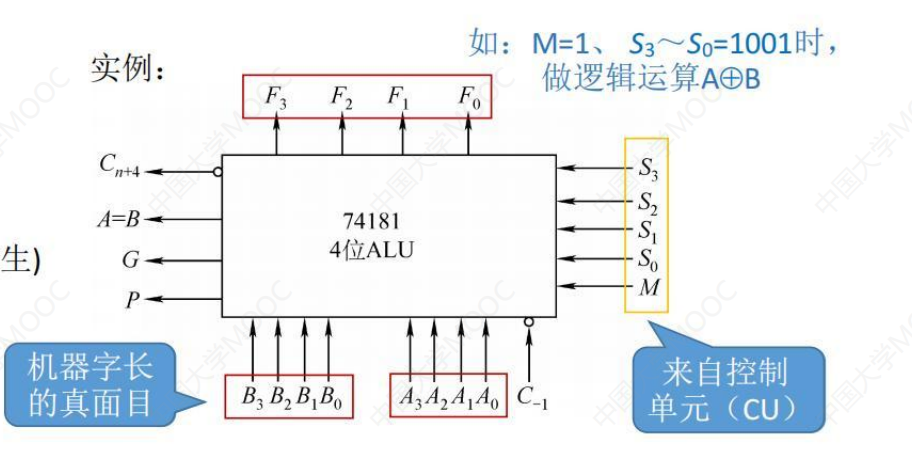
ALU：算术逻辑单元，核心部分是加法器，本质是一些组合逻辑电路，能进行加法运算和与或非这种逻辑运算。

状态寄存器：用于存储一些状态，如溢出标志

通用寄存器组：通用寄存器可用于传送和暂存数据，因为这些寄存器存在，使得计算的中间结果不用存入内存，便于快速读取

移位器：移位

经常说的算术运算是加、减、乘、除，逻辑运算是与、或、非、异或。

通用寄存器的位数就是机器字长，比如输入输出都是4位数据，算出的4位数据也要存入寄存器，所以寄存器的位数一般与机器字长对应。

串行进位加法器就是把一堆全加器串起来，低位运算产生进位所需的时间将影响高位运算的时间，串行进位加法器的最长时间由进位信号传递时间决定，所以加快进位的产生和提高传递的速度是关键。
并行进位加法器不受进位速度影响，但随着加法器位数的增加，电路会越来越复杂（展开式也越来越复杂），所以造出的电路就比较贵。
一般会把串行进位加法器和并行进位加法器结合起来，比如16位的加法器先分成四组，每组组内先行进位，在组间串行进位。
算术逻辑单元ALU是一种组合逻辑电路，能进行加法运算（后面知道加减乘除都能转为加法），也能进行逻辑运算（与或非），当然也能实现左移或者右移的移位操作。

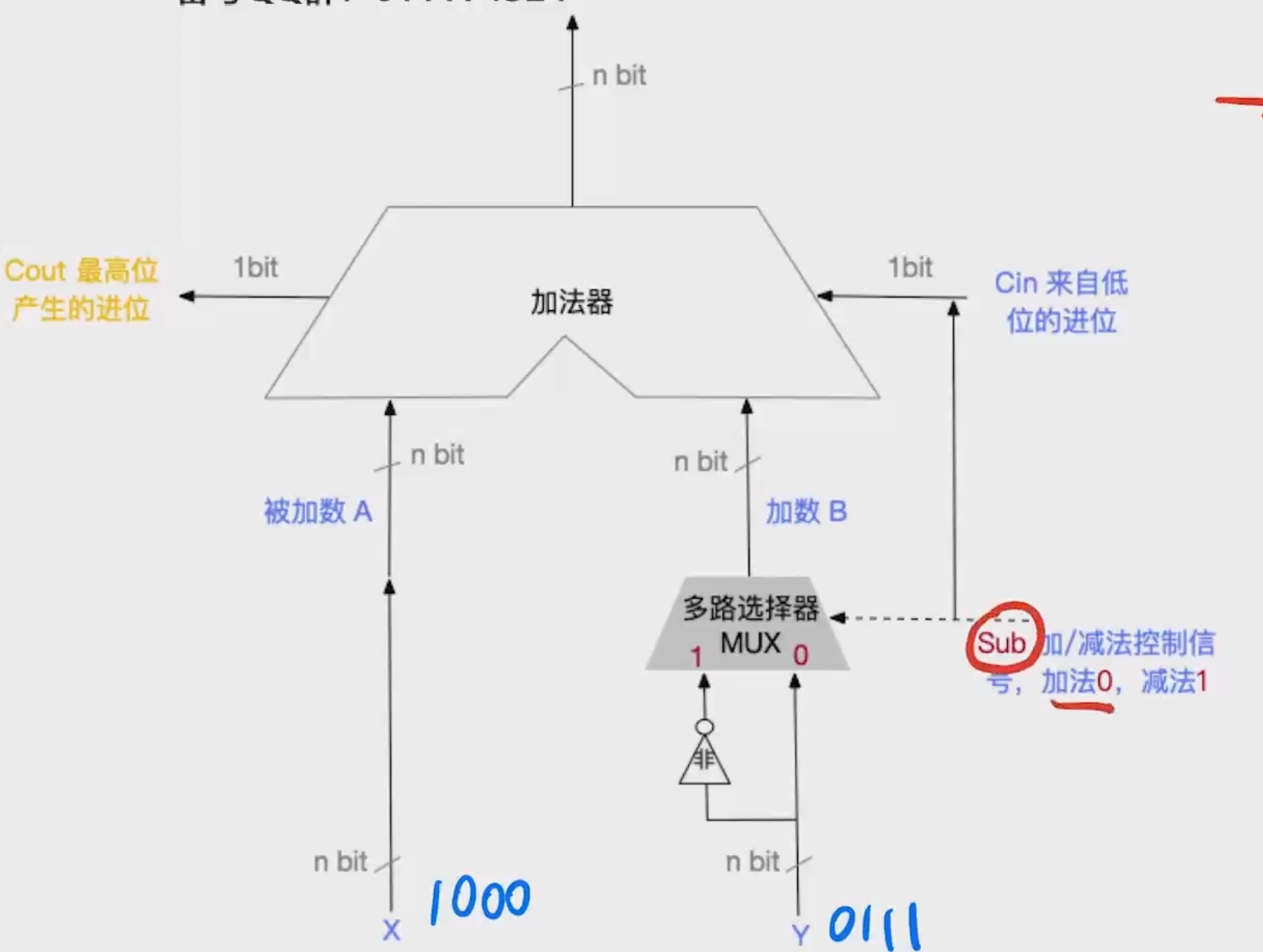
1000+0111的过程

从这个加法器可以知道如果是加法，控制信号Sub取0，然后直接算。如果是减法，那就把减数经过一个非的门电路，达到取反的目的，再将Sub取1，让sub一起进入加法器进行运算，达到取反+1的目的。（取反加一就拿到了这个数的相反数的补码，自然就将减法转成了加法）。加法器的低位进位输入信息值的就是Sub，指的是第一位的进位的前一位。（第一位的进位会参与第二位的运算，而Sub会参与第一位的运算）

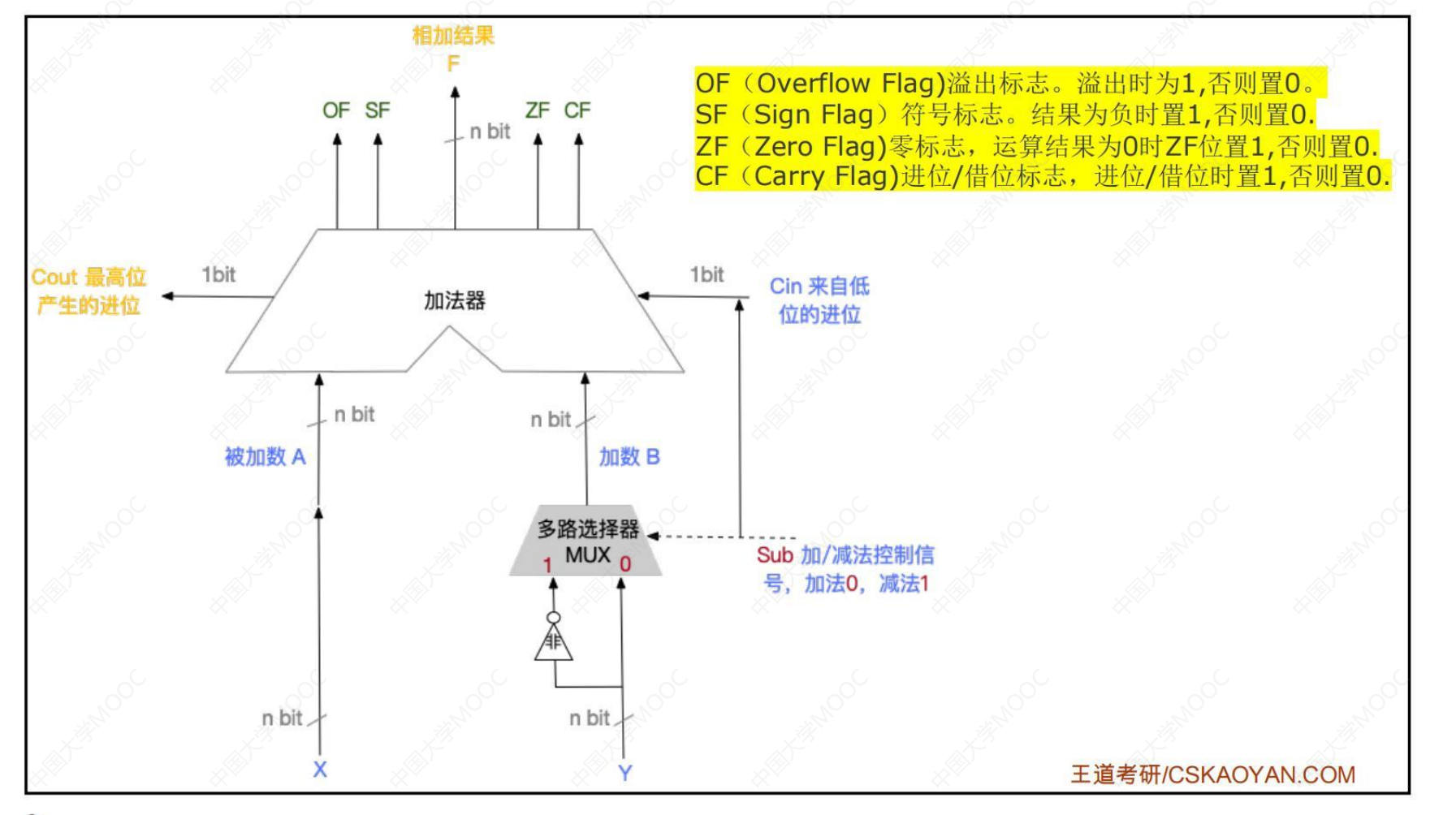
带标志加法器，比如从加法运算结果中获得溢出标志信息

有符号数和无符号的运算方法是一样的，但是判断溢出的方法完全不同。

OF=符号位进位⊕最高数位进位，OF=1时表示带符号整数运算溢出。对无符号运算无意义。

CF=最高位进位⊕Sub,CF=1时表示无符号整数运算溢出。对带符号数运算无意义。

ZF=1表示结果为0，反之则不为0

SF=1表示符号位为1，即为负，反之为正

定点数的移位运算

算术移位

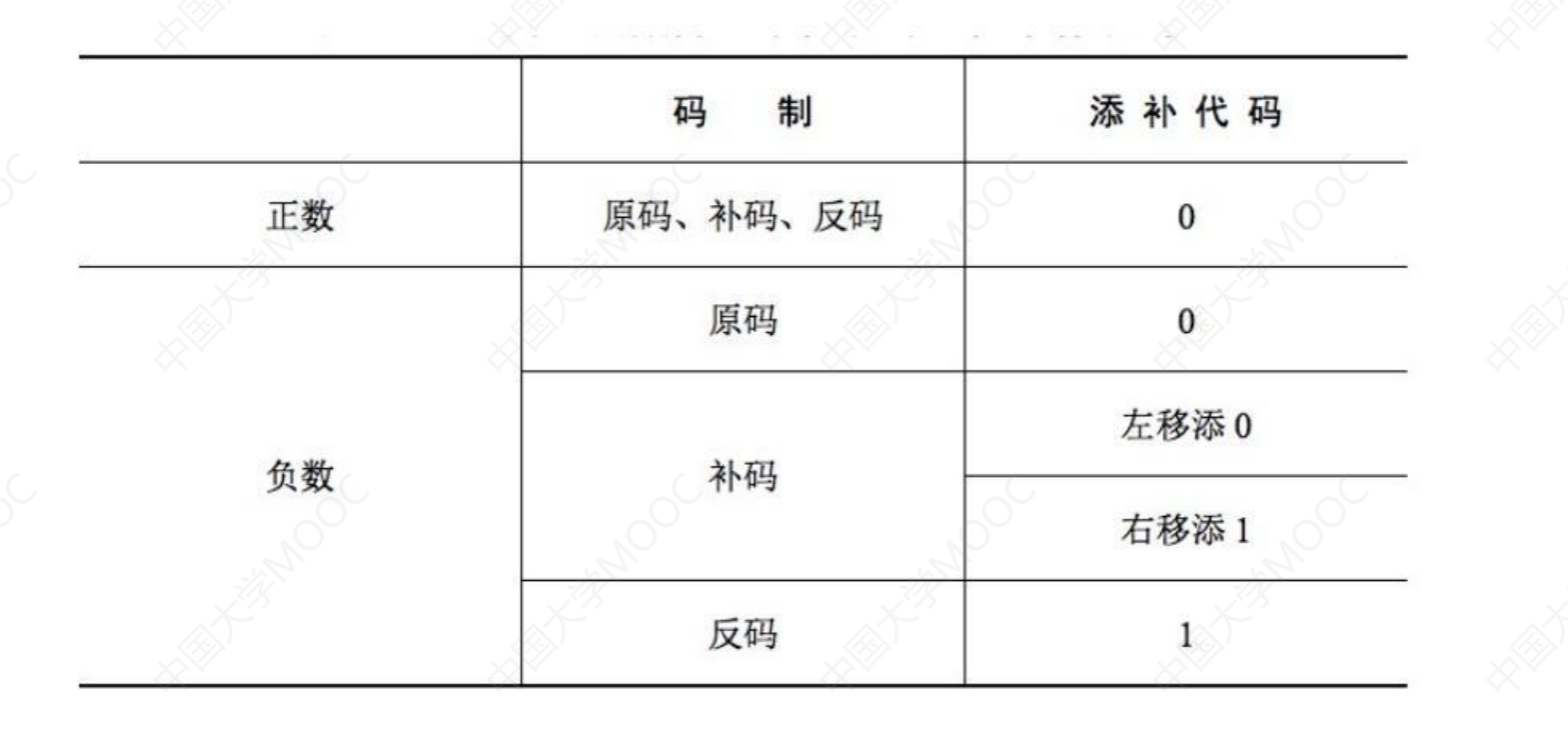
原码算术移位时，符号位不变，不管左移右移补位时都是补0.
反码算术移位时，符号位不变，不管左移右移补位时都是补1.（反码的0就相当于1,1就相当于0）
补码算术移位时，符号位不变，左移补0，右移补符号位。

虽然我们一直说符号位不变，但是双符号移位时，低符号位参与移位，高符号位不参与移位（因为高符号位表示真正的符号）

正数左移时，高位丢1，那就是结果出错（溢出了）。正数右移时低位丢1那就是损失精度。
负数原码左移时，高位丢1，那就是结果出错。负数原码右移时低位丢1那就是损失精度。
负数反码左移时，高位丢0，那就是结果出错，负数反码右移时低位丢0那就是损失精度.
负数补码左移时，高位丢0，那就是结果出错，负数补码右移时低位丢1那就是损失精度（负数补码高位部分像反码，低位部分像原码）

逻辑移位

针对无符号数，左移右移都是补0

循环移位

适合高字节数据和低字节数据互换。

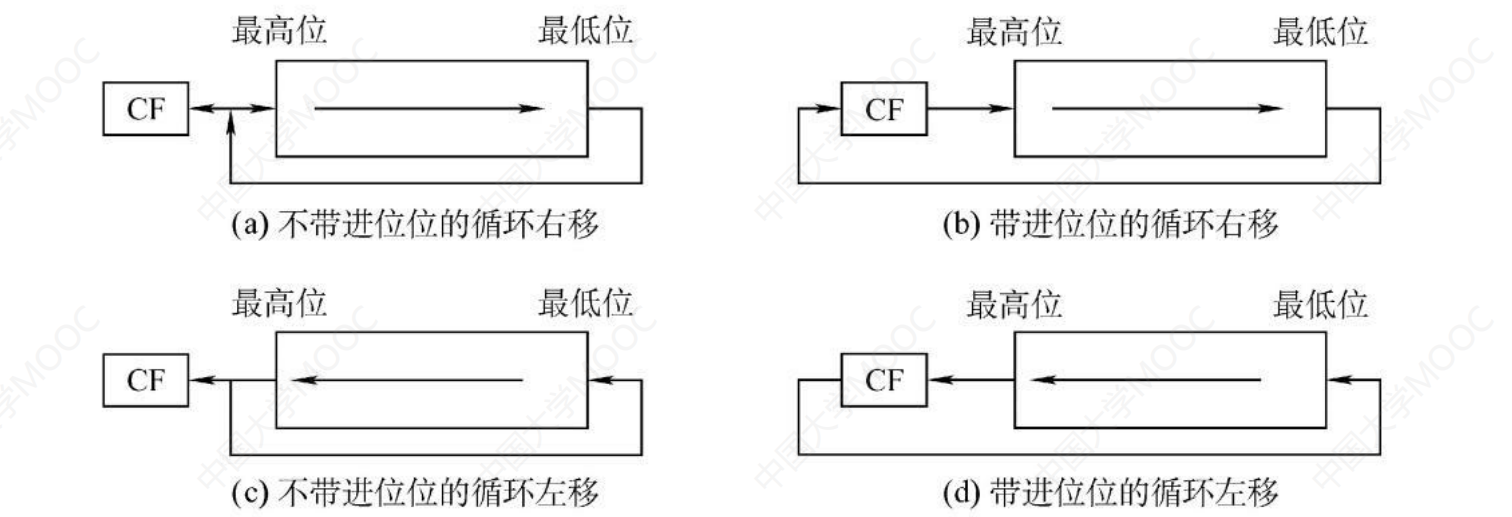
不带进位位时，移出的位还要“赋值"给标志位CF。

带进位位时，CF参与移位。

定点数的加减运算

原码的加减法

符号位相同，则直接绝对值相加，结果的符号位不变

符号位不同，取绝对值相减，结果的符号取决于绝对值大的。（这是我们人可以这么手算，计算机不是这样的）

计算机下原码加减法的处理:

原码的加减法计算规则_原码减法_蔡裕星的博客-CSDN博客

关于为什么减法法则是将减数取补码算，或许可以用补码的定义推。

补码的加减法

在计算机里存储的都是补码，所以补码的加减法很重要，其实补码的加减乘除本质都是加法，也都是用了加法器。

补码的加法

符号位参于运算直接相加，溢出的位丢弃。

补码的减法

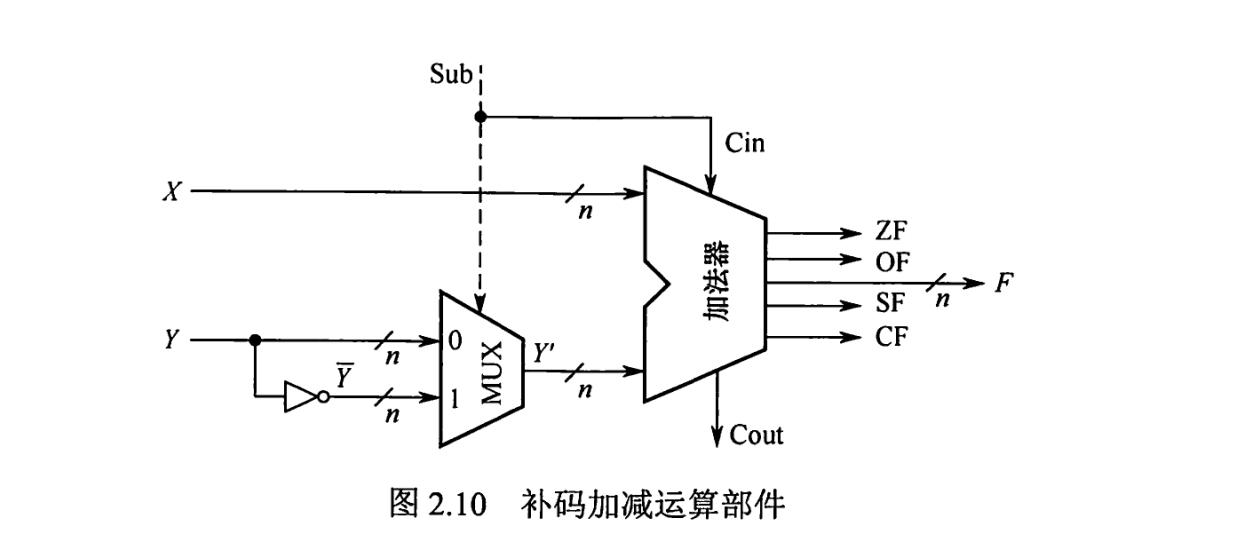
减法转为加法，减去一个数就等于加上这个数的相反数，所以我们拿到减数的负数补码，再直接与被减数相加即可。

获取一个数的负数的补码，全部位取反加1，电路中全部位取反靠门电路实现，加1靠一个控制信号Sub实现。关于要不要取反靠多路选择器（MUX）实现。

溢出的判断

书上写了三种，我只用过两种。

第一种：一位符号位，符号位进位和最高数位进位异或，如果结果为1则溢出，为0则没溢出（显然可以看出这用于有符号数）

第二种：双符号位，00表示是正数且无溢出，01表示结果正溢出，10表示结果负溢出，11表示结果是负数且无溢出。

判断无符号数的溢出，用的是Sub和最高位进位异或的结果，为1表示溢出，为0则没溢出。如果是减法则Sub取1，反之取0.

原码的乘法

这里指的是原码的一位乘法

首先符号位会被单独提出来，不会参与运算。判断符号位是将两个操作数的符号位异或一下，得到的结果就是最终的符号位。

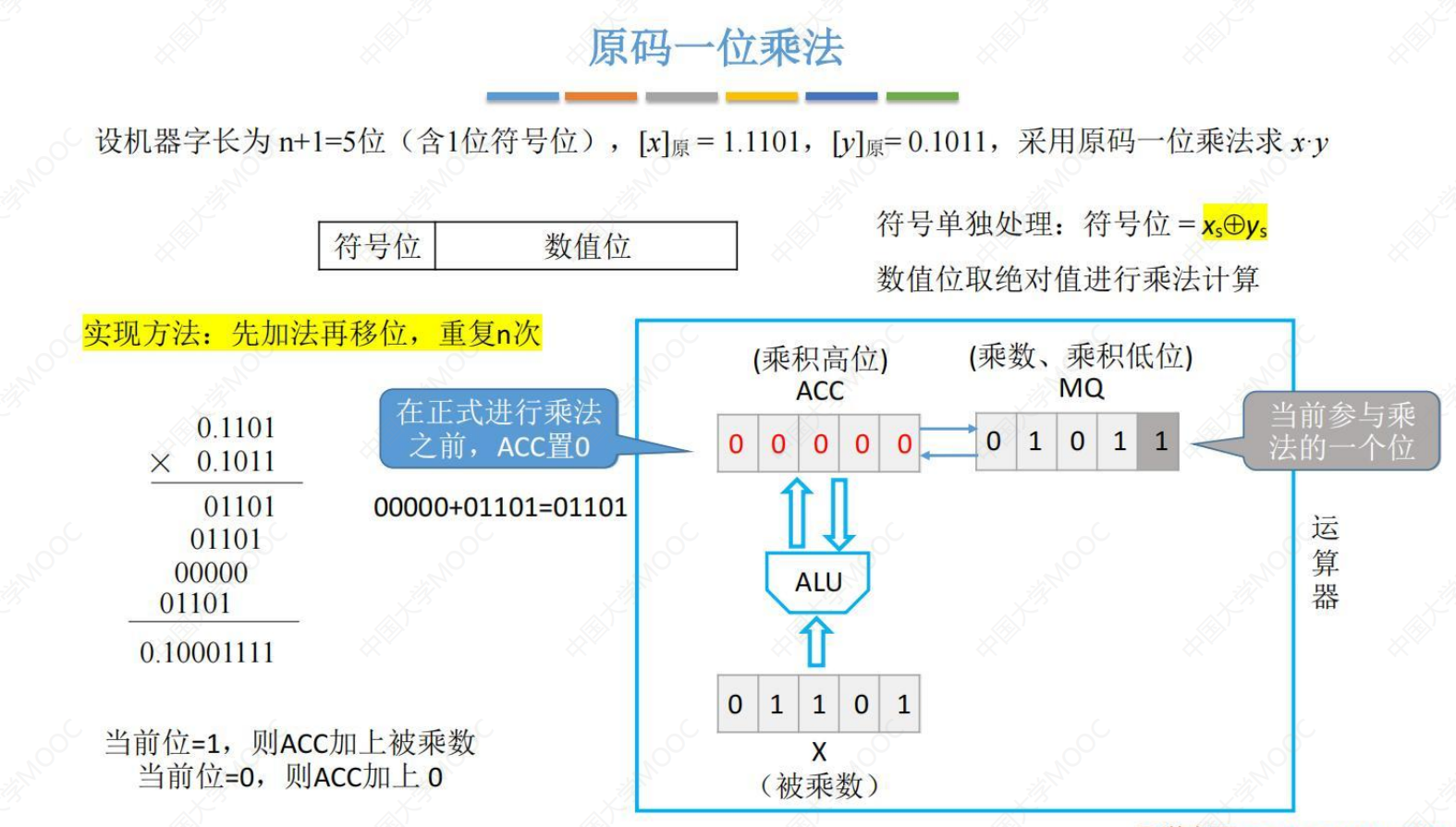
我们在十进制竖式乘法中，也就是手算的算式中知道乘法就是将操作数的每一位乘以另一个操作数的每一位，每一位都可以得到一个部分乘积，再进行错位的相加（通过移位这种操作就能实现错位的效果）。而由于二进制乘法只有01，所以部分乘积的结果要不是0要不就是另一个操作数，再借助加法器就实现了乘法。（这里说的太抽象了，建议去看王道的视频，一步一步带着手算）

机器字长为n+1，则计算n轮,每一轮都要相加和移位。
加x的绝对值还是加0取决于MQ里的最低位。（MQ就是图中的低位部分积/乘数，高位部分积就是ACC）
采用的双符号位，先加法再移位，移位补的永远是0，因为是|x|* |y|,符号位不参与运算
MQ中移出的位不会在结果的结果值里。

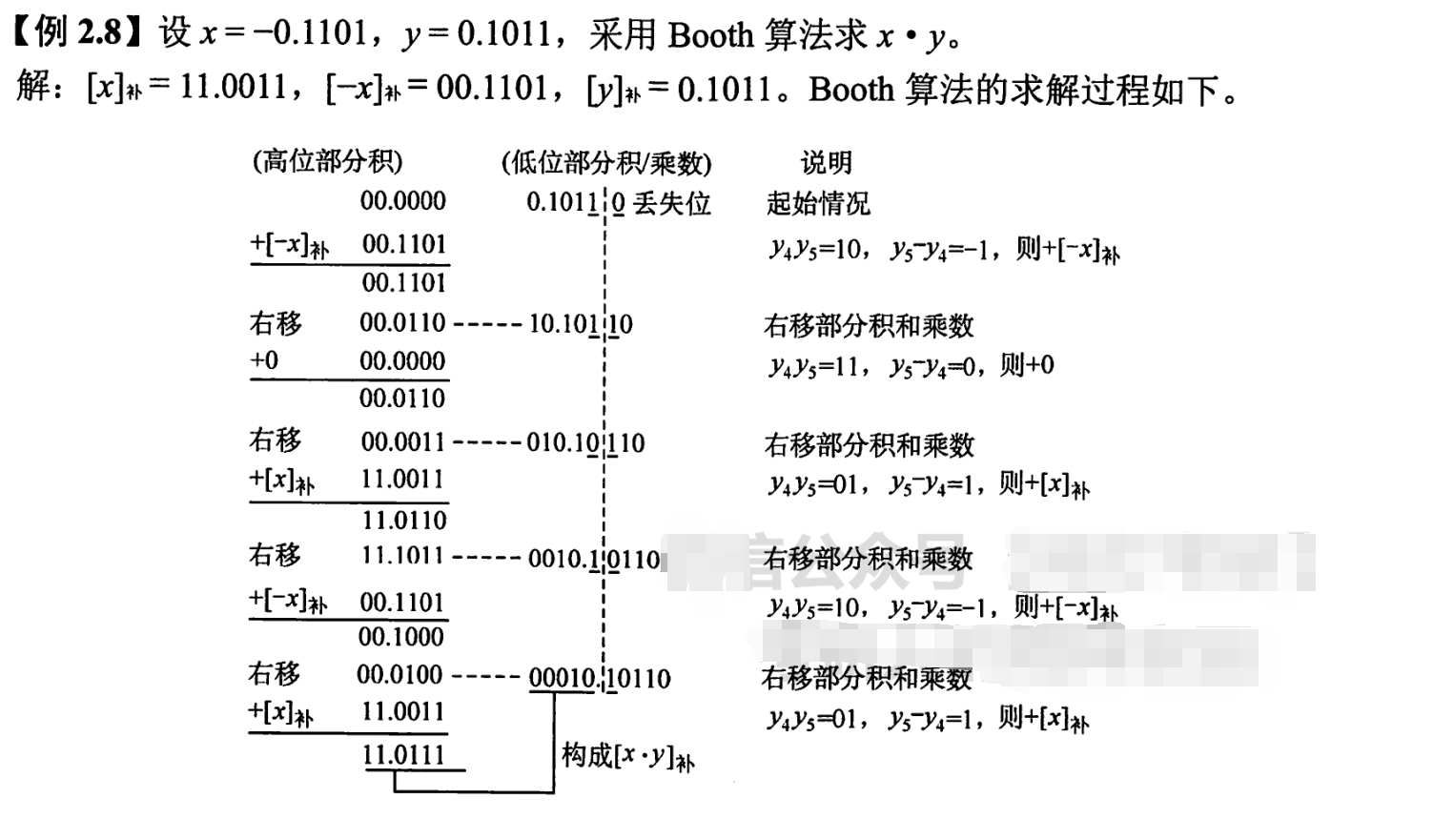
看懂后手算一遍这个例题即可。

补码的乘法

补码的一位乘法也叫Booth算法。

建议看王道的视频。

和原码的乘法很像
符号位参于运算，移位可能补0也可能补1。
机器字长n+1位，会加n+1次，移位n次。最后乘数那块我们画的虚线正好会挨着小数点。
关于每一轮是加[x]_补，还是加[-x]_补，还是加0，取决于辅助位与“MQ最低位”的差（实际上辅助位才是MQ的最低位），如果差为1则加[x]_补，为-1则加[-x]_补，为0则加0.
乘法竖式算出的是[x*y]_补，如果我们求的是x *y的话还得将补码转为原码。

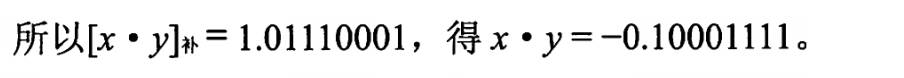
原码的除法

除法有两种办法，一种是恢复余数法，一种是不恢复余数法（加减交替法），不恢复余数法是在恢复余数法的基础上优化来的。

建议看王道视频

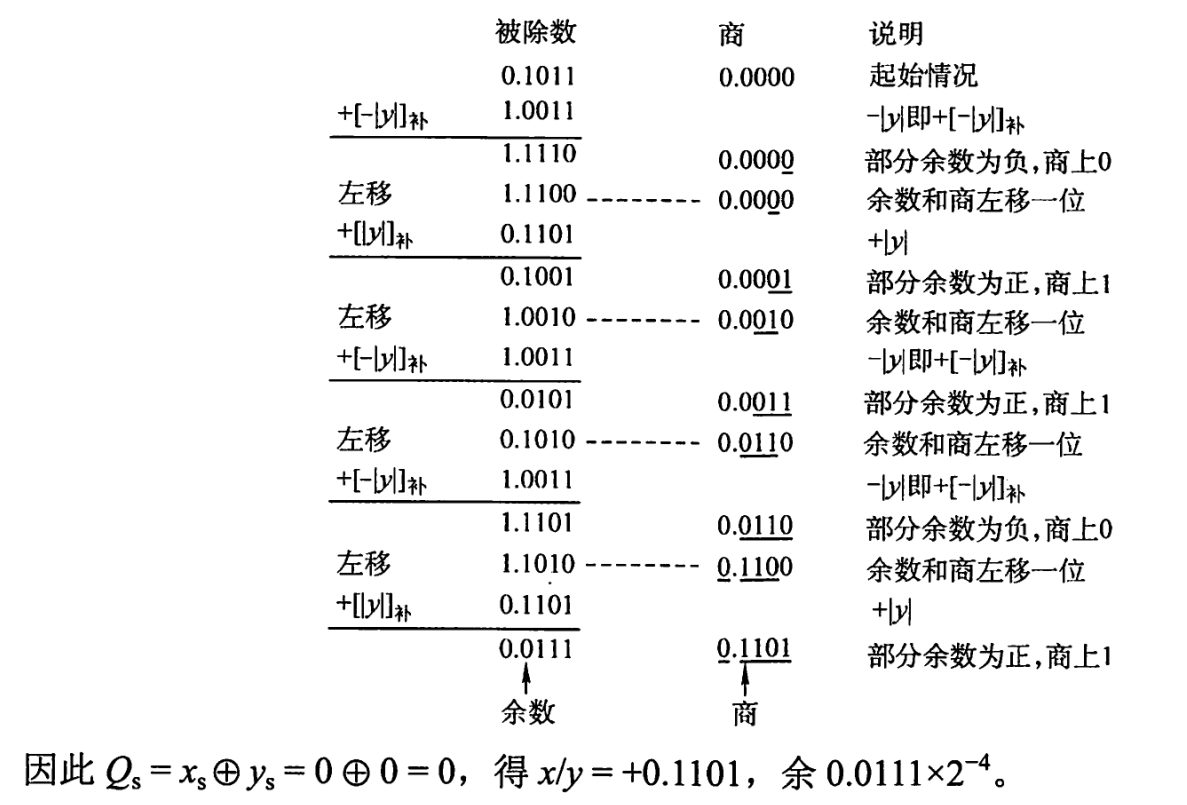
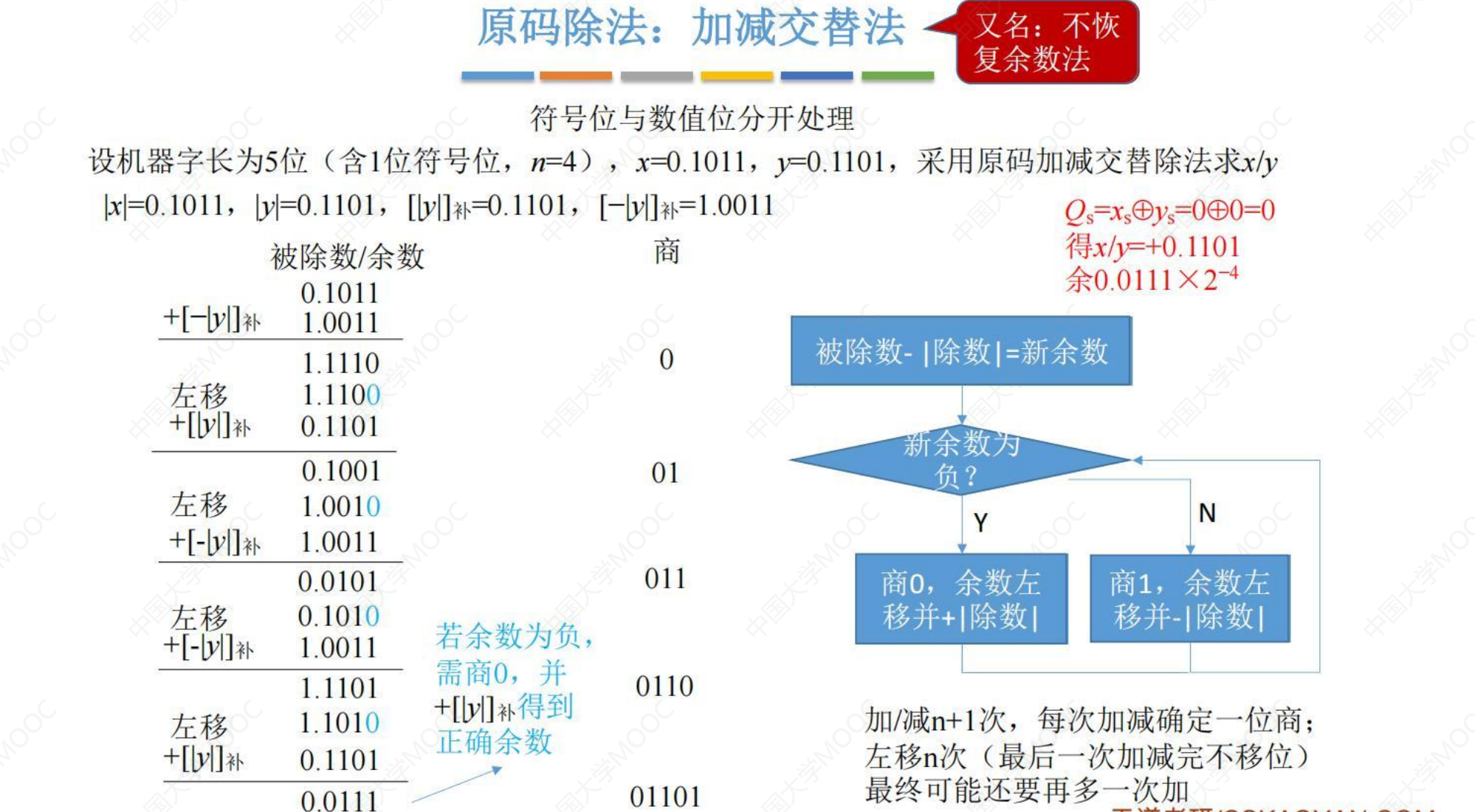
符号位不参与运算，结果的符号位等于两个操作数的符号异或后的结果。
要不加[|y|]_补，要不加[|-y|]_补，最开始是加[|-y|]_补，如果得到的结果如果是正，那就商1，下一次就加[|-y|]_补，如果是负那就商0，下一次就加[|-y|]_补。
机器字长n+1,或者说加符号有n+1位，就要加n+1次，左移n次，注意左移是逻辑左移，所以”符号位“会动。
注意竖式得到的余数还要乘以2^-n才是真正的余数

补码的除法

和原码除法有部分类似

建议看王道视频

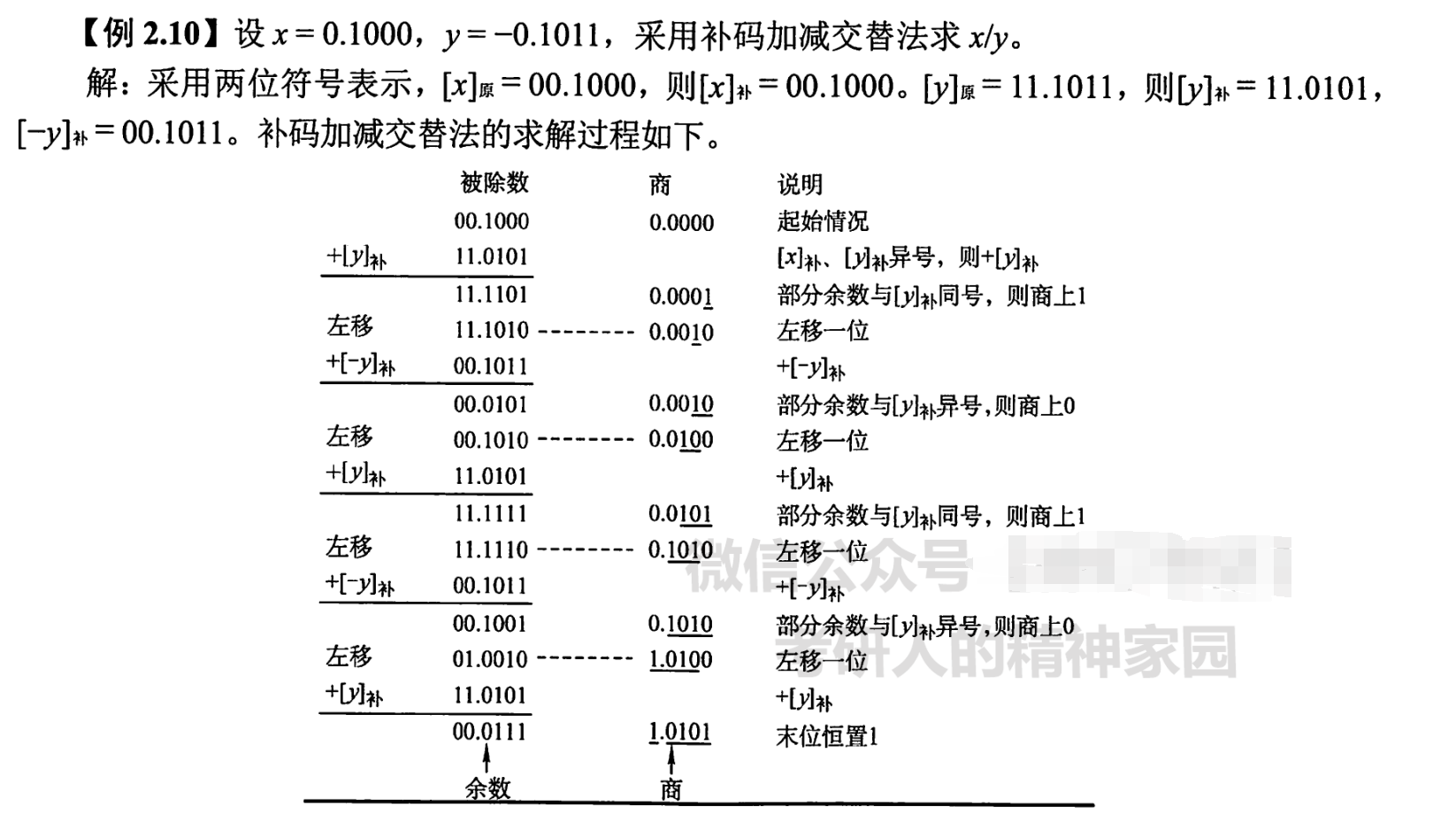
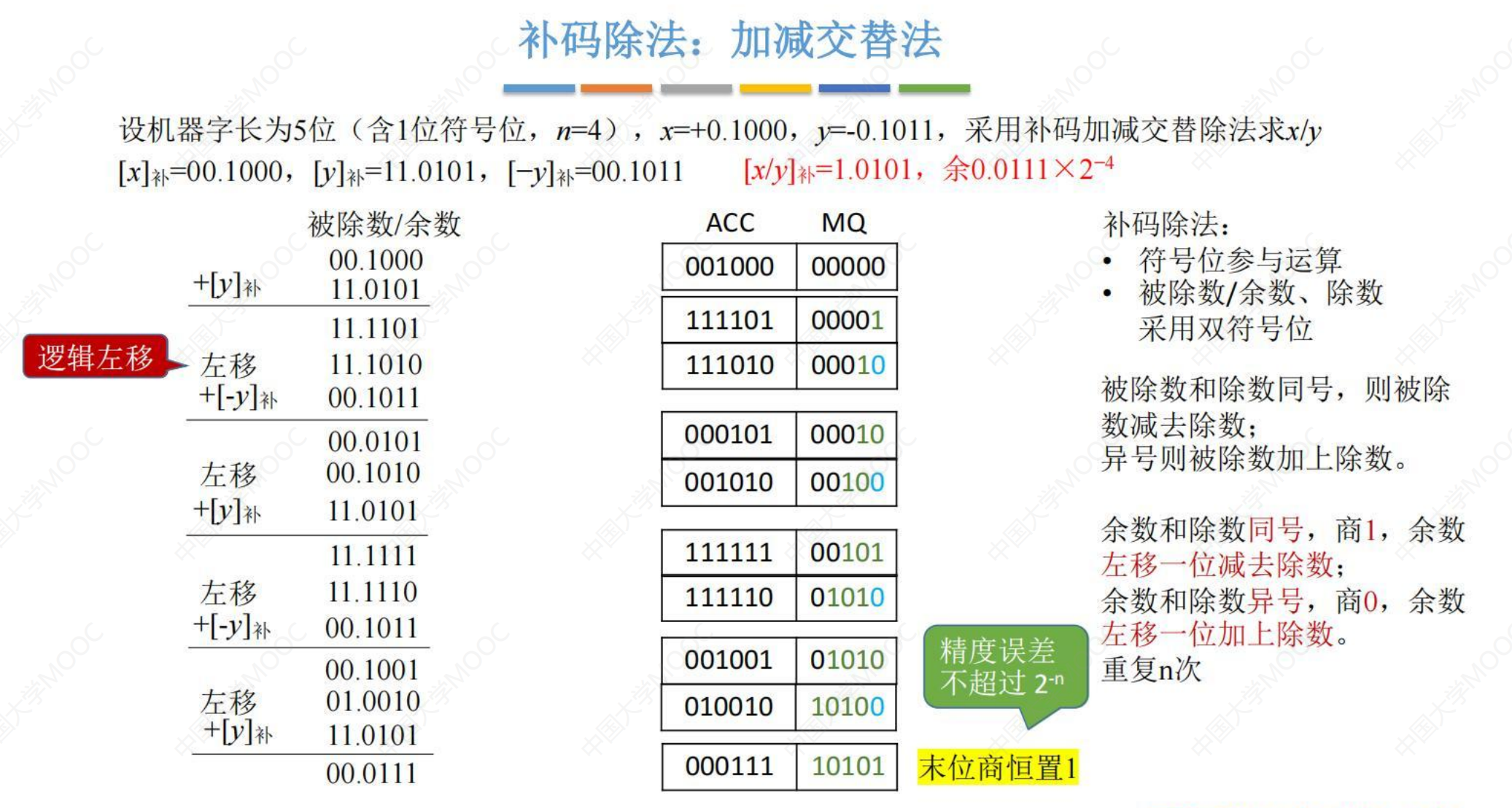
最开始得看被除数和除数的符号决定是加[y]_补,还是加[-y]_补，如果被除数和除数异号则最开始是加[y]_补，如果是同号则加[-y]_补。算出的结果如果与除数同号则商1，之后再加[-y]_补，如果算出的结果与除数异号则商0，再加[y]_补。
移位时是逻辑移位
n+1位的数，加n+1次，移位n次。
ACC里放的余数，MQ里放的商，商最后一位恒置为1.
竖式里得到的余数还得乘以2^-n才是真正的余数，且算出的商和余数都是[x/y]_补。

符号扩展

符号扩展一般指的是补码。

什么时候会发生符号扩展？小字长变量给到大字长变量时就会发生符号扩展。

char ch=127;
int x=ch;//在这个赋值过程中就发生了符号扩展。

符号扩展前后的真值是不变的，正数符号扩展补0，负数符号扩展补1。无符号数的符号扩展统一补0。

负数补码符号扩展补1不会改变真值。

1111 1111扩展为1111 1111 1111 1111 1111 1111 1111 1111 ,扩展前后的真值都是-1。

上面提到了小字长给大字长变量发生符号扩展，那大字长变量给到小字长会发生什么？会发生截断，截断前后真值可能改变，也可能不改变。

如果是相同字长之间的类型转换呢？比如int转为unsigned int会发生什么，比特位都是不变的，只是解释的方式不同了，那么会以无符号数的视角去看这个有符号数，比如-1的补码全1，那此时就是最大的无符号数。

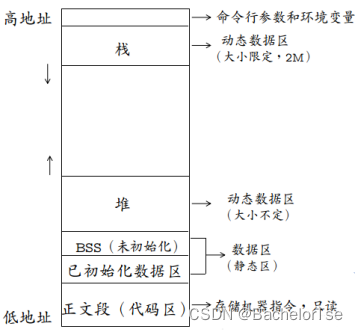
大小端和内存对齐

大端：高位数据存储在低字节，低位数据存储在高字节。如0x11223344（左边是高位，右边是低位），存入内存就是11223344。(左边是低字节，右边是高字节)

小端：高位数据存储在高字节，低位数据存储在低字节。如0x11223344（左边是高位，右边是低位），存入内存就是44332211。(左边是低字节，右边是高字节)

大端适合人看，小端适合机器看。

手把手教你C语言‘数据的存储

内存对齐

复习结构体大小计算以及错题记录_结构体大小计算题_

刷题小结

ALU的本质是组合逻辑电路
地址寄存器不是组成运算器的部件，状态寄存器和通用寄存器属于运算器的一部分。
定点运算器中，无论是采用单符号还是双符号都必须有溢出判断电路，常用异或门来实现。
模4补码，就是双符号位的补码，模2补码，就是单符号位的补码
双符号位比起单符号位更容易检查出加减法的溢出，存储模4补码时只需存储一位符号位，因为只有双符号的第一位表示真正的符号,另外一位的作用倾向于判断溢出，但是在ALU这些算术与逻辑部件中需要存储两位符号位，这样运算也没那么容易溢出。