目录
机器学习术语
标签
特性
示例
模型
回归与分类
深入了解机器学习:线性回归
深入了解机器学习:训练和损失
平方损失函数:一种常用的损失函数
机器学习术语
预计用时:8 分钟
什么是(监督式)机器学习?简而言之,如下所示:
- 机器学习系统学习如何组合输入以对从未见过的数据生成有用的预测。
我们来探索一下机器学习的基本术语。
标签
标签是指我们要预测的内容,即简单线性回归中的 y 变量。标签可以是小麦的未来价格、图片中显示的动物类型、音频剪辑的含义,也可以是其他任何信息。
特性
特征是输入变量,即简单线性回归中的 x 变量。一个简单的机器学习项目可能会使用单个功能,而更复杂的机器学习项目可以使用数百万个功能,如下所示:
在垃圾邮件检测器示例中,这些功能可能包括:
- 电子邮件文字中的字词
- 发件人的地址
- 发送电子邮件的时间
- 电子邮件中包含词组“一种奇怪的技巧”。
示例
样本是指数据的特定实例:x。(我们将 x 显示为粗体,表示它是一个矢量。)我们将示例分为两类:
- 有标签样本
- 无标签样本
有标签样本同时包含特征和标签。具体来说:
labeled examples: {features, label}: (x, y)
使用有标签样本来训练模型。在我们的垃圾邮件检测器示例中,有标签样本是指用户明确标记为“垃圾邮件”或“不是垃圾邮件”的个别电子邮件。
例如,下表显示了从包含加利福尼亚州房价信息的数据集中获取的 5 个有标签样本:
| homeMedianAge (功能) | 会议室总数 (设施) | 卧室总数 (设施) | medianHouseValue (标签) |
|---|---|---|---|
| 15 | 5612 | 1283 | 66900 |
| 19 | 7650 | 1901 | 80100 |
| 17 | 720 | 174 | 85700 |
| 14 | 1501 | 337 | 73400 |
| 20 | 1454 | 326 | 65500 |
无标签样本包含特征,但不包含标签。具体来说:
unlabeled examples: {features, ?}: (x, ?)
以下是来自同一住房数据集的 3 个无标签样本(不包括 medianHouseValue):
| homeMedianAge (功能) | 会议室总数 (设施) | 卧室总数 (设施) |
|---|---|---|
| 42 | 1686 | 361 |
| 34 | 1226 | 180 |
| 33 | 1077 | 271 |
使用有标签样本训练模型后,我们便会使用该模型来预测无标签样本的标签。在垃圾邮件检测器中,无标签样本是用户尚未添加标签的新电子邮件。
模型
模型定义了特征和标签之间的关系。例如,垃圾内容检测模型可能会将某些功能与“垃圾内容”紧密关联。我们重点介绍模型生命周期的两个阶段:
-
训练是指创建或学习模型。也就是说,您向模型展示有标签样本,让模型逐渐学习特征与标签之间的关系。
-
推断表示将经过训练的模型应用于无标签样本。也就是说,使用经过训练的模型做出有用的预测 (
y')。例如,在推理期间,您可以针对新的无标签样本预测medianHouseValue。
回归与分类
回归模型可预测连续值。例如,回归模型做出的预测可回答如下问题:
-
加利福尼亚州一栋房子的价值是多少?
-
用户点击此广告的可能性有多大?
分类模型可预测离散值。例如,分类模型做出的预测可回答如下问题:
-
指定的电子邮件是垃圾邮件还是非垃圾邮件?
-
这是狗、猫还是仓鼠的图片?
关键术语
|
|
|
|
|
|
|
|
深入了解机器学习:线性回归
预计用时:6 分钟
长久以来,人们都知道板球(昆虫物种)在天气炎热的日子里会比在更冷的日子里鸣叫。数十年来,专业和业余科学家一直在编制每分钟的鸣叫声和温度方面的数据。Ruth 大姨妈给您送上生日祝福,送上一份生日礼物,邀请您学习一个模型来预测这种关系。 您想利用这些数据来探索这种关系。
首先,通过绘制数据的方式检查数据:
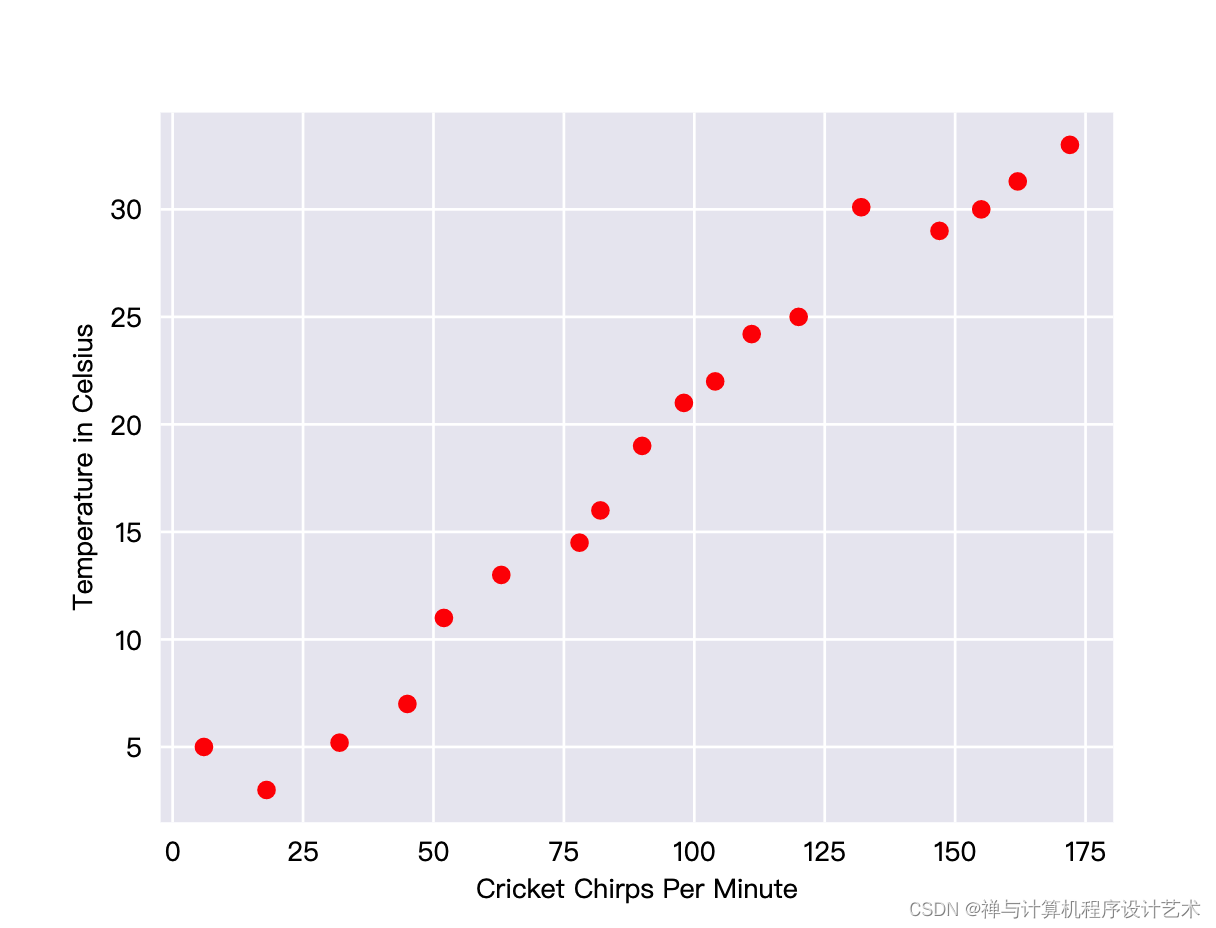
图 1. 每分钟的鸣叫声与温度(以摄氏度为单位)。
如您所料,该图表显示了温度随着鸣叫声次数的增加而上升。 鸣叫声与温度之间的关系是线性关系吗?可以,您可以绘制一条直线来大致说明这种关系:

图 2. 一种线性关系。

关键术语
|
|
|
|
深入了解机器学习:训练和损失
预计用时:6 分钟
训练模型只需从有标签样本中学习(确定)所有权重和偏差的理想值。在监督式学习中,机器学习算法通过检查许多示例并尝试找到将损失降至最低的模型来构建模型;此过程称为经验风险最小化。
损失是错误预测的惩罚。也就是说,损失是一个表示模型在单个样本上的预测质量的数字。如果模型的预测完全准确,则损失为零,否则损失会更大。训练模型的目的是从所有样本中找到一组平均损失“较小”的权重和偏差。例如,图 3 左侧显示的是高损失模型,右侧显示的是低损失模型。对于该图,请注意以下几点:
- 箭头表示损失。
- 蓝线表示预测。
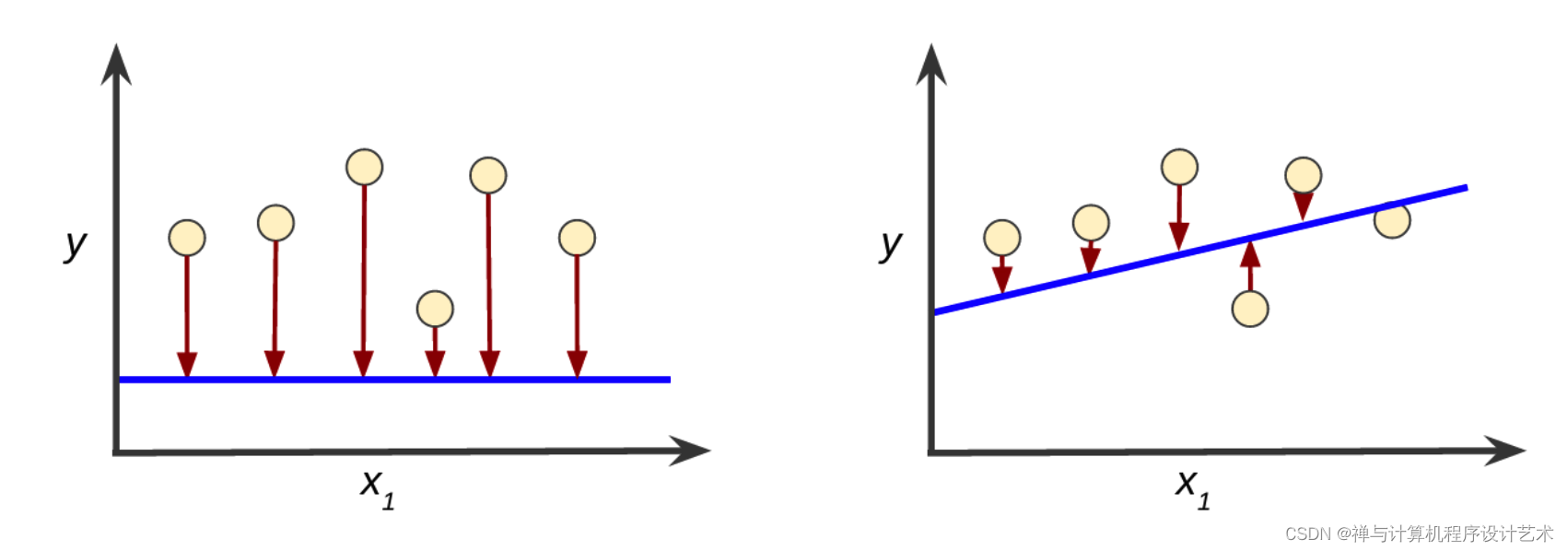
图 3. 左侧模型中的损失较高;右侧模型中的损失较低。
请注意,左侧曲线图中的箭头比右侧曲线图中的箭头长得多。显然,相较于左侧曲线图中的线条,右侧曲线图中的预测模型要好得多。
您可能想知道是否可以创建数学函数(损失函数),以有意义的方式汇总各个损失。
平方损失函数:一种常用的损失函数
我们在此探讨的线性回归模型使用一种称为平方损失函数(也称为 L2 损失)的损失函数。单个样本的平方损失如下:
= the square of the difference between the label and the prediction = (observation - prediction(x))2 = (y - y')2

关键术语
|
|
|
|
|
https://developers.google.com/machine-learning/crash-course/ml-intro?hl=zh-cn