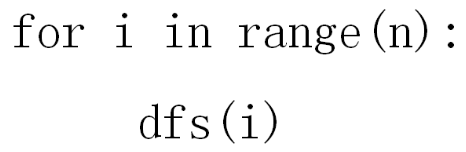目录
一、前言
二、图的概念
三、例题及相关概念
1、全球变暖(2018年省赛,lanqiao0J题号178)
2、欧拉路径
3、小例题
4、例题(洛谷P7771)
一、前言
本文主要讲了树与图的基本概念,图的存储、DFS遍历,欧拉路与欧拉回路以及相关例题。
二、图的概念
- 图:由点 (node,或者vertex) 和连接点的边 (edge) 组成。
- 图是点和边构成的网。
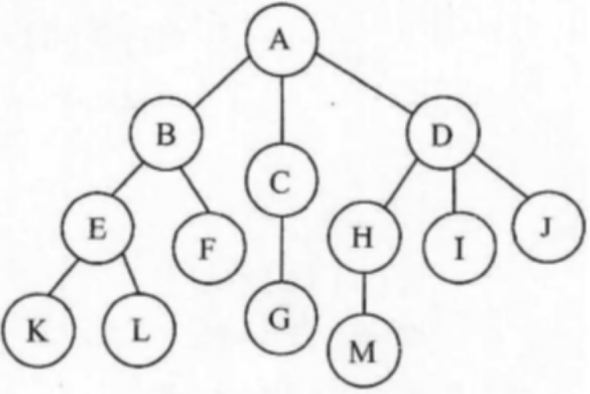
- 树 (是一种特殊的图),即连通无环图
- 树的结点从根开始,层层扩展子树,是一种层次关系,这种层次关系,保证了树上不会出现环路。
- 两点之间的路径:有且仅有一条路径。
【图算法的复杂度】
- 和边的数量E、点的数量V相关。
- O(V+E):几乎是图问题中能达到的最好程度。
- O(VlogE)、O(ElogV):很好的算法。
- O(v^2)、O(E^2)或更高:不算是好的算法。
- 例:最短路径、树的LCA(最近公共祖先)
【图的存储】
能快速访问:图的存储,能让程序很快定位结点 u 和 v 的边 (u,v)。
- 数组存边:简单、空间使用最少;无法快递定位
- 邻接矩阵:简单、空间使用最大;定位最快
- 邻接表:空间很少,定位较快
- 链式前向星:空间更少,定位较快
【数组存边】
优点:简单、最省空间。
缺点:无法定位某条边。
应用:最小生成树的kruskal算法
e=[] for i in range(m): u,v,w=map(int,input().split()) e.append((u,v,w))【邻接矩阵】
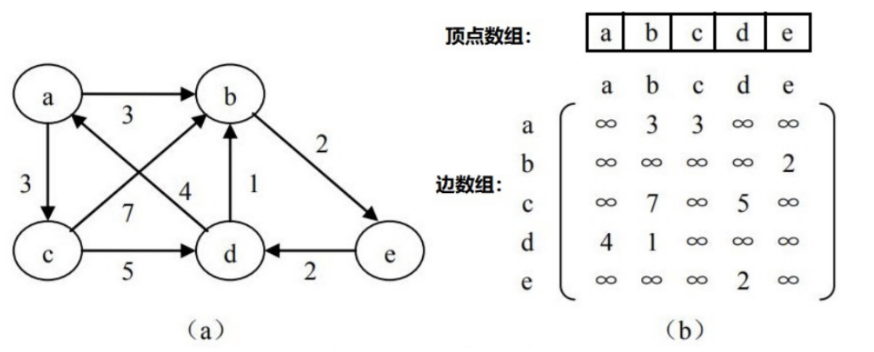
- 二维数组:graph[NUM][NUM]
- 无向图:graph[i][j] = graph[j][i]
- 有向图:graph[i][j] != graph[j][i]
- 权值:graph[i][j] 存结点 i 到 j 的边的权值。例如 graph[1][2]=3,graph[2][1]=5 等等
- 用 graph[i][j]=INF 表示 i,j 之间无边。
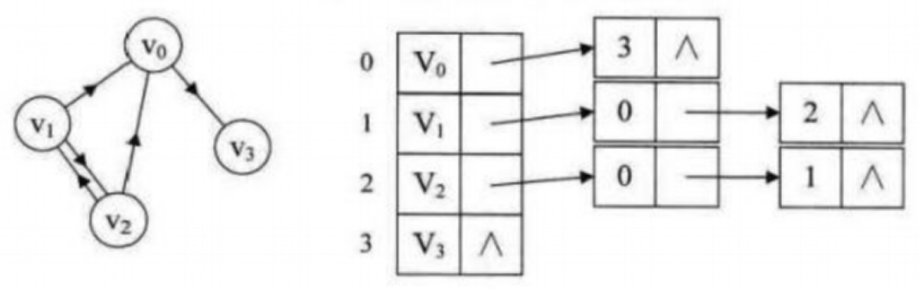
【邻接表】
- 应用场景:大稀疏图
- 优点:
- 存储效率非常高,存储复杂度 O(V+E)
- 能存储重边
edge=[[] for i in range(N+1)] #定义邻接表 for i in range(N): u,v,w=map(int,input().split()) #读入点u,v和边长w edge[u].append((v,w)) edge[v].append((u,w)) #无向边 for v,w in edge[u]:【链式前向星】
空间极端紧张,紧凑的存图方法。
相关内容见另一篇博客。
链式前向星_链式前向星 csdn_吕同学的头发不能秃的博客-CSDN博客
【图的遍历和连通性】
- BFS 和 DFS:图论的基本算法。
- 图论算法,或者直按用 BFS 和 DFS 来解决问题,或者用其思想建立新的算法。
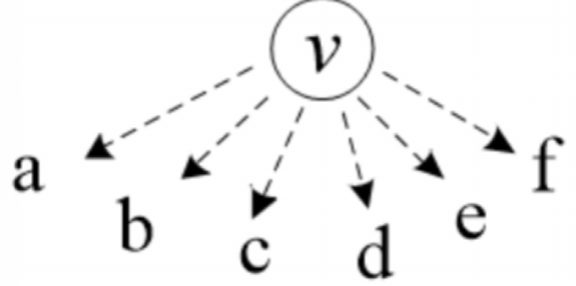
【如何遍历非连通图】
想象有个虛拟结点 v,它连接了所有点
在主程序中对这些点逐一进行 dfs()
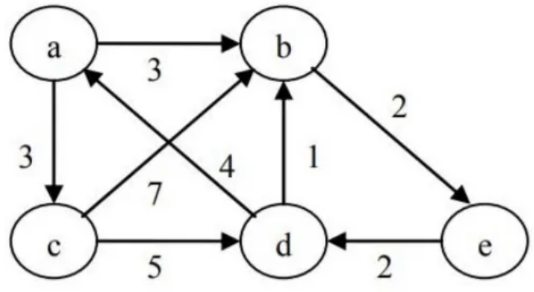
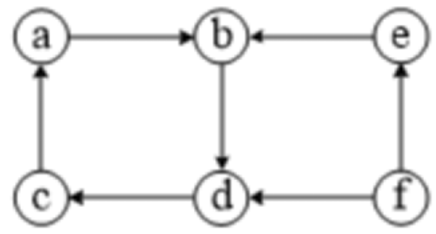
【用DFS判断连通性】
- 对需要的点执行 dfs(),就能找到它连通的点。
- 并查集也能用于检查连通性。
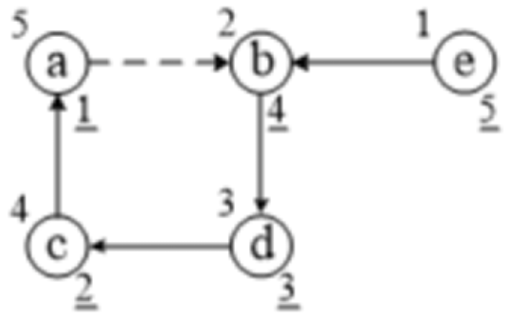
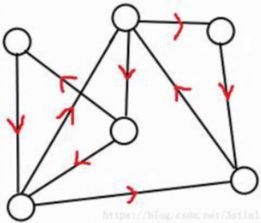
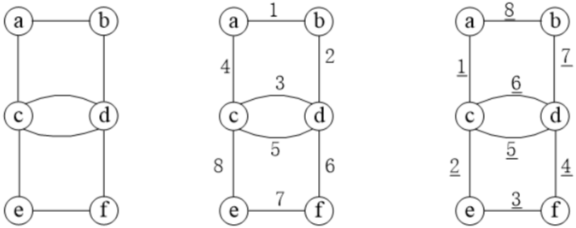
找 e 点的连通性:执行 dfs(e)。
- 访问过程:见结点上面的数字,顺序是:e, b, d, c, a
- 递归返回的结果:见结点下面划线数字,顺序是:a, c, d, b, e
三、例题及相关概念
1、全球变暖(2018年省赛,lanqiao0J题号178)
该题目在我写DFS的笔记时就讲过。
见连接:DFS排列组合与连通性_排列组合dfs_吕同学的头发不能秃的博客-CSDN博客
另外我也独立写了一个题解,后面一对和链接里面的很类似。
import sys
sys.setrecursionlimit(65000)
def dfs(x,y):
global vis
global m
global flag
global N
vis[x][y]=-1
d=[(-1,0),(1,0),(0,-1),(0,1)]
if m[x-1][y]=='#' and m[x+1][y]=='#' and \
m[x][y-1]=='#' and m[x][y+1]=='#':
flag=1
for i in range(4):
dx=x+d[i][0]
dy=y+d[i][1]
if dx<0 or dx>=N or dy<0 or dy>=N:
continue
if vis[dx][dy]==0 and m[dx][dy]=='#':
dfs(dx,dy)
N=int(input())
vis=[[0]*(N+1) for _ in range(N+1)]
m=[]
for _ in range(N):
m.append(list(input()))
cnt=0
for i in range(1,N-1):
for j in range(1,N-1):
if vis[i][j]==0 and m[i][j]=='#':
flag=0
dfs(i,j)
if flag==0:
cnt+=1
print(cnt)
2、欧拉路径
【欧拉路】
- 欧拉路:从图中某个点出发,遍历整个图,图中每条边通过且只通过一次。
- 欧拉回路:起点和终点相同的欧拉路。
欧拉路问题:
1)是否存在欧拉路
2)打印出欧拉路
通过处理度 (degree):一个点上连接的边的数量,称为这个点的度数。
在无向图中,如果度数是奇数,这个点称为奇点,否则称为偶点。
【欧拉路和欧拉回路是否存在】
1)无向连通图的判断条件如果图中的点全都是偶点,则存在欧拉回路;任意一点都可以作为起点和终点。如果只有 2 个奇点,则存在欧拉路,其中一个奇点是起点,另一个是终点。不可能出现有奇数个奇点的无向图。
2)有向连通图的判断条件
把一个点上的出度记为 1,入度记为 -1,这个点上所有出度和入度相加,就是它的度数。一个有向图存在欧拉回路,当且仅当该图所有点的度数为零。如果只有一个度数为 1 的点,一个度数为 -1的点,其它所有点的度数为0, 那么存在欧拉路径,其中度数为 1 的是起点,度数为 -1 的是终点。
3、小例题
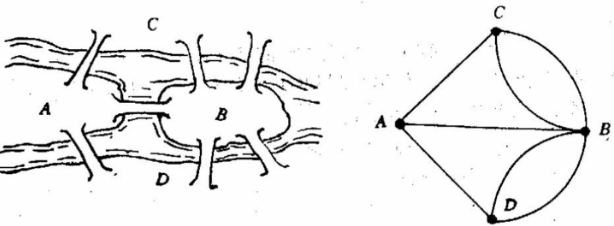
有 n 个珠子。每个珠子有两种颜色,分布在珠子的两边。一共有 50 种不同的颜色。把这些珠子串起来,要求两个相邻的珠子接触的那部分颜色相同。问是否能连成一个珠串项链?如果能,打印一种连法。
- 答:这一题是典型的无向图求欧拉回路。首先,判断所有的点是否为偶点,如果存在奇点,则没有欧拉回路;其次,判断所给的图是否连通,不连通也不是欧拉回路。
【输出一个欧拉回路】
对一个无向连通图做 DFS,就输出了一个欧拉回路。
【DFS与欧拉回路】
DFS的结果是一个欧拉回路。
4、例题(洛谷P7771)
原题链接:【模板】欧拉路径 - 洛谷
【题目描述】
求有向图字典序最小的欧拉路径
【输入格式】
第一行 2 个整数 n、m,表示有向图的点数和边数。下面 m 行,每行 2 个整数 u、v,表示存在一个有向边边 u->v
【输出格式】
如果不存在欧拉路径,输出一行 No。
否则输出一行 m+1 个数字,表示字典序最小的欧拉路径。
python题解只能过60%
import sys
def dfs(u):
i=d[u] #从点u的第一条边i=0开始
while i<len(G[u]):
d[u]=i+1 #后面继续走u的下一条边
dfs(G[u][i]) #继续走这条边的邻居点
i=d[u] #第一条边走过了,不再重复走
rec.append(u)
M=100010
n,m=map(int,input().split())
du=[[0 for _ in range(2)] for _ in range(M)] #记录每个点的入度、出度
G=[[] for _ in range(n+5)] #邻接表存图
d=[0 for _ in range(M)] #d[u]=i;当前走u的第i个边
rec=[] #记录欧拉路
for i in range(m):
u,v=map(int,input().split())
G[u].append(v)
du[u][1]+=1 #出度
du[v][0]+=1 #入度
for i in range(1,n+1):
G[i].sort() #对邻居点排序,字典序
S=1
cnt=[0,0]
flg=True
for i in range(1,n+1):
if du[i][1]!=du[i][0]: #当出度≠入度时,该点就为奇点,此时图存在奇点
flg=False
if du[i][1]-du[i][0]==1:
cnt[1]+=1 #cnt[1]用于统计起点数
S=i
if du[i][0]-du[i][1]==1:
cnt[0]+=1
if (not flg) and (not (cnt[0]==cnt[1] and cnt[0]==1)): #存在奇点,且不是只有一个起点和一个终点
print("No",end='')
sys.exit(0)
dfs(S)
rec=rec[::-1] #反过来,回溯的顺序是欧拉路
#print(''.join(str(i) for i in rec))
print(rec[0],end='')
for i in range(1,len(rec)):
print(" %d"%rec[i],end='')
print()
以上,图论初入门
祝好