题目链接

Leetcode.2359 找到离给定两个节点最近的节点 Rating ： 1715

题目描述

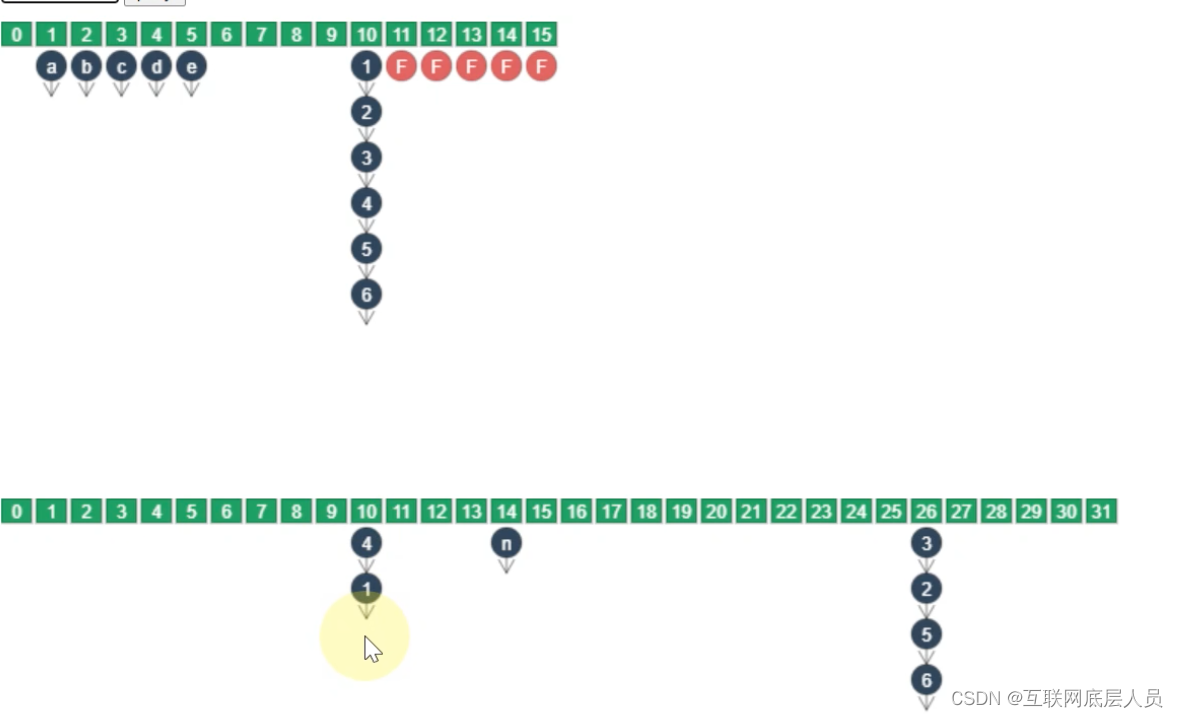
给你一个 n个节点的 有向图 ，节点编号为 0到 n - 1，每个节点 至多 有一条出边。

有向图用大小为 n下标从 0开始的数组 edges表示，表示节点 i有一条有向边指向 edges[i]。如果节点 i没有出边，那么 edges[i] == -1。

同时给你两个节点 node1和 node2。

请你返回一个从 node1和 node2都能到达节点的编号，使节点 node1和节点 node2到这个节点的距离 较大值最小化。如果有多个答案，请返回 最小 的节点编号。如果答案不存在，返回 -1。

注意 edges可能包含环。

示例1：

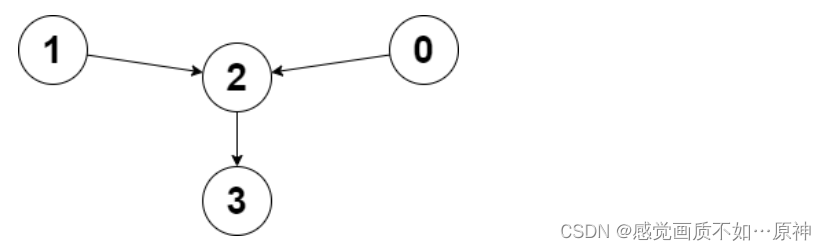
输入：edges = [2,2,3,-1], node1 = 0, node2 = 1
输出：2
解释：从节点 0 到节点 2 的距离为 1 ，从节点 1 到节点 2 的距离为 1 。
两个距离的较大值为 1 。我们无法得到一个比 1 更小的较大值，所以我们返回节点 2 。

示例2：

输入：edges = [1,2,-1], node1 = 0, node2 = 2
输出：2
解释：节点 0 到节点 2 的距离为 2 ，节点 2 到它自己的距离为 0 。
两个距离的较大值为 2 。我们无法得到一个比 2 更小的较大值，所以我们返回节点 2 。

提示：

• $n==edges.length$
• $2<=n<=10^5$
• $-1<=edges[i]<n$
• $edges[i]!=i$
• $0<=node1,node2<n$

解法一：BFS

一个比较容易想到的解法是，对于 node1和 node2分别通过 BFS 计算其 到各个点的距离矩阵 d1和 d2。

对于 d1和 d2，我们从小到大遍历，更新最小的 较大值。

时间复杂度：$O(n)$

代码：

class Solution {
public:
// 建图
    unordered_map<int,vector<int>> g;
    
    //bfs 求起点 root 到各个点的距离矩阵
    void bfs(int root,vector<int> & dist){
        queue<int> q;
        q.push(root);

        int step = 0;
        while(!q.empty()){
            int sz = q.size();
            for(int i = 0;i < sz;i++){
                auto t = q.front();
                q.pop();
                dist[t] = step;

                for(auto v:g[t]){
                    if(dist[v] != -1) continue;
                    q.push(v);
                }
            }
            step++;
        }
    }

    int closestMeetingNode(vector<int>& edges, int node1, int node2) {
        int n = edges.size();
        for(int i = 0;i < n;i++){
            if(edges[i] == -1) continue;

            int a = i, b = edges[i];
            g[a].push_back(b);
        }
        

        vector<int> a(n,-1),b(n,-1);

        bfs(node1,a);
        bfs(node2,b);

        /*for(int i = 0;i < n;i++){
            printf("i = %d , d1 = %d , d2 = %d\n",i,a[i],b[i]);
        }*/

        int dist = 1e9;
        int idx = -1;

        for(int i = 0;i < n;i++){
            if(a[i] == -1 || b[i] == -1) continue;
            int d = max(a[i],b[i]);
            if(dist > d){
                dist = d;
                idx = i;
            }
        }

        return idx;
    }
};

解法二：遍历

题目给定地有向图实际上是一个 基环树，因为每一个结点的 出边最多只有一条，所以实际上我们不需要建图，只需要直接循环遍历即可。

时间复杂度：$O(n)$

代码：

class Solution {
public:
    int closestMeetingNode(vector<int>& edges, int node1, int node2) {
        int n = edges.size();

        auto dfs = [&](int u) -> vector<int>{
            vector<int> dist(n,1e9);
            int d = 0;

            while(u != -1 && dist[u] == 1e9){
                dist[u] = d;
                d++;
                u = edges[u];
            }

            return dist;
        };

        auto d1 = dfs(node1);
        auto d2 = dfs(node2);

        int ans = 1e9,idx = -1;
        for(int i = 0;i < n;i++){
            if(d1[i] == 1e9 || d2[i] == 1e9) continue;
            int d = max(d1[i],d2[i]);
            if(ans > d){
                ans = d;
                idx = i;
            }
        }
        return idx;
    }
};