动规
- 剑指 Offer 10- I. 斐波那契数列
- 动态规划
- 动态规划的优化【两种赋值】
- 剑指 Offer 10- II. 青蛙跳台阶问题
- 剑指 Offer 63. 股票的最大利润
- 考虑效率优化【时间+空间】
- python初始化无穷大或无穷小值
写在前面:
动规分析必备:状态定义、状态转移方程、初始状态和返回值。
考虑动规的优化:在第i项只与少数项有关时,用少数几个变量代替可降低复杂度。
剑指 Offer 10- I. 斐波那契数列
题:写一个函数,输入 n ,求斐波那契(Fibonacci)数列的第 n 项(即 F(N))。斐波那契数列的定义如下:
F(0) = 0, F(1) = 1
F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
斐波那契数列由 0 和 1 开始,之后的斐波那契数就是由之前的两数相加而得出。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
动态规划
状态定义:dp[i]表示第 i 项的斐波那契数列。
状态转移:dp[i] = dp[i - 1] + dp[i -2],题目已经给了。
初始值:dp[0] = 0, dp[1] = 1。
返回值:dp[n]。
class Solution:
def fib(self, n: int) -> int:
dp=[]
dp.append(0)
dp.append(1)
for i in range(2,n+1):
dp.append((dp[i-1]+dp[i-2])%1000000007)
return dp[n]%1000000007
时间复杂度:O(n),遍历一次。
空间复杂度:O(n),dp 数组需要占用 O(n)O(n)O(n) 的额外空间。
动态规划的优化【两种赋值】
所谓动态规划的优化,就是找状态转移的过程中第 i 项到底跟哪些项有关,如果关联的项比较少的话,就可以使用少数的几个变量代替,比如这题中 i 的状态只与 i - 1 和 i - 2 有关,所以,我们只需要声明 3 个变量轮动就可以了。
class Solution:
def fib(self, n: int) -> int:
#2)dp优化
if n<=1:return n
a,b=0,1
for i in range(2,n+1):
tmp=b
b=(a+b)%1000000007
a=tmp
return b
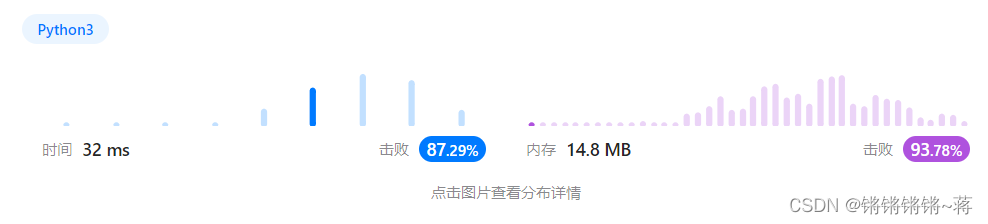
另一种赋值方式不同:
#3)dp优化
if n<=1:return n
a,b=0,1
for i in range(2,n+1):
tmp=(a+b)%1000000007
a=b
b=tmp
return tmp
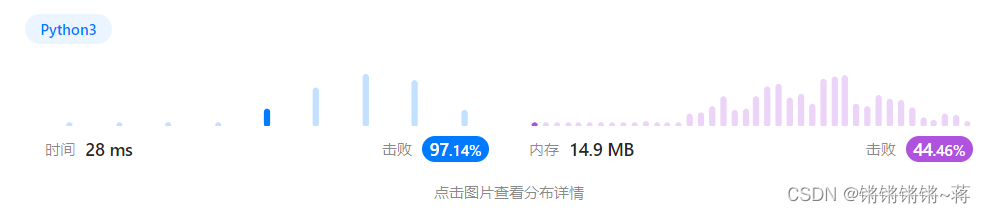
剑指 Offer 10- II. 青蛙跳台阶问题
一只青蛙一次可以跳上1级台阶,也可以跳上2级台阶。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
跟前面一题不同的就是dp[0]=1,其余一样的
class Solution:
def numWays(self, n: int) -> int:
dp=[]
dp.append(1)
dp.append(1)
for i in range(2,n+1):
dp.append((dp[i-1]+dp[i-2])%1000000007)
return dp[n]
剑指 Offer 63. 股票的最大利润
题:假设把某股票的价格按照时间先后顺序存储在数组中,请问买卖该股票一次可能获得的最大利润是多少?
示例 1:
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。
直接参考题解吧QAQ: 股票的最大利润(动态规划,清晰图解)
考虑效率优化【时间+空间】

Q:dp[i]跟dp[i-1]有关,为什么用一个变量profit代替整个dp数组哇?!(不懂,动规好难)
class Solution:
def maxProfit(self, prices: List[int]) -> int:
cost, profit = float("+inf"), 0
for price in prices:
cost = min(cost, price)
profit = max(profit, price - cost)
return profit
python初始化无穷大或无穷小值
float(“INF”)表示为正无穷; float(“-INF”)表示负无穷